Nội Dung
Hướng dẫn giải Bài §4. Phép nhân đa thức một biến sgk Toán 7 tập 2 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 5 trang 63 sgk Toán 7 tập 2 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
§4. PHÉP NHÂN ĐA THỨC MỘT BIẾN
Câu hỏi khởi động trang 60 Toán 7 tập 2 CD
Trong quá trình biến đổi và tính toán những biểu thức đại số, nhiều khi ta phải thực hiện phép nhân hai đa thức một biến, chẳng hạn ta cần thực hiện phép nhân sau:
\((x – 1)({x^2} + x + 1)\)
Làm thế nào để thực hiện được phép nhân hai đa thức một biến?
Trả lời:
Muốn nhân một đa thức với một đa thức, ta nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia rồi cộng các tích với nhau.
I. NHÂN ĐƠN THỨC VỚI ĐƠN THỨC
Hoạt động 1 trang 60 Toán 7 tập 2 CD
Thực hiện phép tính:
a) \({x^2}.{x^4}\);
b) \(3{x^2}.{x^3}\);
c) \(a{x^m}.b{x^n}\) (a ≠ 0; b ≠ 0; m, n \(\in\) N).
Trả lời:
a) Ta có:
\({x^2}.{x^4} = {x^{2 + 4}} = {x^6}\).
b) Ta có:
\(3{x^2}.{x^3} = 3.1.{x^{2 + 3}} = 3{x^5}\).
c) Ta có:
\(a{x^m}.b{x^n} = a.b.{x^{m + n}}\) (a ≠ 0; b ≠ 0; m, n \(\in\) N).
Luyện tập vận dụng 1 trang 60 Toán 7 tập 2 CD
Tính:
a) \(3{x^5}.5{x^8}\);
b) \( – 2{x^{m + 2}}.4{x^{n – 2}}\) (m, n \(\in\) N; n > 2).
Trả lời:
a) Ta có:
\(3{x^5}.5{x^8} = 3.5.{x^5}.{x^8} \\= 15.{x^{5 + 8}} = 15.{x^{13}}\).
b) Ta có:
\( – 2{x^{m + 2}}.4{x^{n – 2}} = – 2.4.{x^{m + 2}}.{x^{n – 2}} \\= – 8.{x^{m + 2 + n – 2}} = – 8.{x^{m + n}}\) (m, n \(\in\) N; n > 2).
II. NHÂN ĐƠN THỨC VỚI ĐA THỨC
Hoạt động 2 trang 60 Toán 7 tập 2 CD
Quan sát hình chữ nhật MNPQ ở Hình 3.
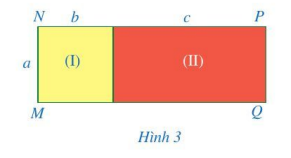
a) Tính diện tích mỗi hình chữ nhật (I), (II);
b) Tính diện tích của hình chữ nhật MNPQ;
c) So sánh: \(a(b + c)\) và \(ab + ac\).
Trả lời:
a) Diện tích của hình chữ nhật (I) là: \(a.b\).
Diện tích của hình chữ nhật (II) là: \(a.c\).
b) Diện tích của hình chữ nhật MNPQ là: \(ab + ac\).
c) Ta có:
\(a(b + c) = a.b + a.c\).
Vậy \(a(b + c)\) = \(ab + ac\).
Hoạt động 3 trang 61 Toán 7 tập 2 CD
Cho đơn thức \(P(x) = 2x\) và đa thức \(Q(x) = 3{x^2} + 4x + 1\).
a) Hãy nhân đơn thức P(x) với từng đơn thức của đa thức Q(x).
b) Hãy cộng các tích vừa tìm được.
Trả lời:
a) Các đơn thức của đa thức Q(x) là: \(3{x^2}; 4x; 1\).
Tích của đơn thức P(x) với từng đơn thức của đa thức Q(x) lần lượt là:
\(2x.3{x^2} = 6{x^3};\\2x.4x = 8{x^2};\\2x.1 = 2x\).
b) Cộng các tích vừa tìm được:
\(6{x^3} + 8{x^2} + 2x\).
Luyện tập vận dụng 2 trang 61 Toán 7 tập 2 CD
Tính:
a) \(\dfrac{1}{2}x(6x – 4)\);
b) \( – {x^2}(\dfrac{1}{3}{x^2} – x – \dfrac{1}{4})\).
Trả lời:
a) Ta có:
\(\dfrac{1}{2}x(6x – 4) = \dfrac{1}{2}x.6x + \dfrac{1}{2}x.( – 4) = 3{x^2} – 2x\).
b) Ta có:
$ – {x^2}(\dfrac{1}{3}{x^2} – x – \dfrac{1}{4}) = – {x^2}.\dfrac{1}{3}{x^2} + – {x^2}. – x + – {x^2}. – \dfrac{1}{4}\\ = – \dfrac{1}{3}{x^4} + {x^3} + \dfrac{1}{4}{x^2}$
III. NHÂN ĐA THỨC VỚI ĐA THỨC
Hoạt động 4 trang 61 Toán 7 tập 2 CD
Quan sát hình chữ nhật MNPQ ở Hình 4.
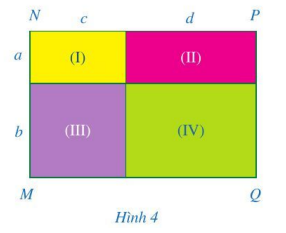
a) Tính diện tích mỗi hình chữ nhật (I), (II), (III), (IV).
b) Tính diện tích của hình chữ nhật MNPQ.
c) So sánh: \((a + b)(c + d)\) và \(ac + ad + bc + bd\).
Trả lời:
a) Diện tích của hình chữ nhật (I) là: \(a.c\).
Diện tích của hình chữ nhật (II) là: \(a.d\).
Diện tích của hình chữ nhật (III) là: \(b.c\).
Diện tích của hình chữ nhật (IV) là: \(b.d\).
b) Diện tích hình chữ nhật MNPQ là:
\(ac + ad + bc + bd\).
c) Ta có:
\((a + b)(c + d) = a(c + d) + b(c + d) = ac + ad + bc + bd\).
Vậy \((a + b)(c + d) = ac + ad + bc + bd\).
Hoạt động 5 trang 62 Toán 7 tập 2 CD
Cho đa thức \(P(x) = 2x + 3\) và đa thức \(Q(x) = x + 1\).
a) Hãy nhân mỗi đơn thức của đa thức P(x) với từng đơn thức của đa thức Q(x).
b) Hãy cộng các tích vừa tìm được.
Trả lời:
a) Các đơn thức của đa thức P(x) là: \(2x;3\).
Các đơn thức của đa thức Q(x) là: \(x;1\).
Tích mỗi đơn thức P(x) với từng đơn thức của đa thức Q(x) lần lượt là: \(2{x^2}; 2x; 3x; 3\).
b) Cộng các tích vừa tìm được:
\(2{x^2} + 2x + 3x + 3 = 2{x^2} + 5x + 3\).
Luyện tập vận dụng 3 trang 62 Toán 7 tập 2 CD
Tính:
a) \(({x^2} – 6)({x^2} + 6)\);
b) \((x – 1)({x^2} + x + 1)\).
Trả lời:
a) Ta có:
$({x^2} – 6)({x^2} + 6) = {x^2}({x^2} + 6) + ( – 6).({x^2} + 6) \\= {x^2}.{x^2} + {x^2}.6) + ( – 6).{x^2} + ( – 6).6\\ = {x^4} + 6{x^2} – 6{x^2} – 36 \\= {x^4} – 36$
b) Ta có:
$(x – 1)({x^2} + x + 1) = x({x^2} + x + 1) + ( – 1)({x^2} + x + 1) \\= x.{x^2} + x.x + x.1 + ( – 1).{x^2} + ( – 1).x + ( – 1).1\\ = {x^3} + {x^2} + x – {x^2} – x – 1 \\= {x^3} – 1$
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 5 trang 63 sgk Toán 7 tập 2 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 63 Toán 7 tập 2 CD
Tính:
a) \(\dfrac{1}{2}{x^2}.\dfrac{6}{5}{x^3}\);
b) \({y^2}(\dfrac{5}{7}{y^3} – 2{y^2} + 0,25)\);
c) \((2{x^2} + x + 4)({x^2} – x – 1)\);
d) \((3x – 4)(2x + 1) – (x – 2)(6x + 3)\).
Bài giải:
a) Ta có:
\(\dfrac{1}{2}{x^2}.\dfrac{6}{5}{x^3} = \dfrac{1}{2}.\dfrac{6}{5}.{x^2}.{x^3} = \dfrac{3}{5}{x^5}\).
b) Ta có:
${y^2}(\dfrac{5}{7}{y^3} – 2{y^2} + 0,25) = {y^2}.\dfrac{5}{7}{y^3} – {y^2}.2{y^2} + {y^2}.0,25\\ = \dfrac{5}{7}{y^5} – 2{y^4} + 0,25{y^2}$.
c) Ta có:
$(2{x^2} + x + 4)({x^2} – x – 1) \\= 2{x^2}({x^2} – x – 1) + x({x^2} – x – 1) + 4({x^2} – x – 1)\\ = 2{x^4} – 2{x^3} – 2{x^2} + {x^3} – {x^2} – x + 4{x^2} – 4x – 4 \\= 2{x^4} – {x^3} + {x^2} – 5x – 4$.
d) Ta có:
$(3x – 4)(2x + 1) – (x – 2)(6x + 3) \\= 3x(2x + 1) – 4(2x + 1) – x(6x + 3) + 2(6x + 3)\\ = 6{x^2} + 3x – 8x – 4 – 6{x^2} – 3x + 12x + 6\\ = 4x + 2$.
Giải bài 2 trang 63 Toán 7 tập 2 CD
Tìm bậc, hệ số cao nhất và hệ số tự do của mỗi đa thức:
a) \(P(x) = ( – 2{x^2} – 3x + x – 1)(3{x^2} – x – 2)\);
b) \(Q(x) = ({x^5} – 5)( – 2{x^6} – {x^3} + 3)\).
Bài giải:
a) Ta có:
$P(x) = ( – 2{x^2} – 3x + x – 1)(3{x^2} – x – 2) \\= – 2{x^2}(3{x^2} – x – 2) – 3x(3{x^2} – x – 2) + x(3{x^2} – x – 2) – 1.(3{x^2} – x – 2)\\ = – 6{x^4} + 2{x^3} + 4{x^2} – 9{x^3} + 3{x^2} + 6x + 3{x^3} – {x^2} – 2x – 3{x^2} + x + 2\\ = – 6{x^4} – 4{x^3} + 3{x^2} + 5x + 2$.
Bậc của đa thức là: $4$.
Hệ số cao nhất của đa thức là: $– 6$.
Hệ số tự do của đa thức là: $2$.
b) Ta có:
$Q(x) = ({x^5} – 5)( – 2{x^6} – {x^3} + 3) \\= {x^5}( – 2{x^6} – {x^3} + 3) – 5( – 2{x^6} – {x^3} + 3) \\= – 2{x^{11}} – {x^8} + 3{x^5} + 10{x^6} + 6{x^3} – 15\\ = – 2{x^{11}} – {x^8} + 10{x^6} + 3{x^5} + 6{x^3} – 15$.
Bậc của đa thức là: $11$.
Hệ số cao nhất của đa thức là: $– 2$.
Hệ số tự do của đa thức là: $– 15$.
Giải bài 3 trang 63 Toán 7 tập 2 CD
Xét đa thức \(P(x) = {x^2}({x^2} + x + 1) – 3x(x – a) + \dfrac{1}{4}\) (với a là một số).
a) Thu gọn đa thức P(x) rồi sắp xếp đa thức đó theo số mũ giảm dần của biến.
b) Tìm a sao cho tổng các hệ số của đa thức P(x) bằng \(\dfrac{5}{2}\).
Bài giải:
a) Ta có:
$P(x) = {x^2}({x^2} + x + 1) – 3x(x – a) + \dfrac{1}{4} \\= {x^4} + {x^3} + {x^2} – 3{x^2} + 3ax + \dfrac{1}{4}\\ = {x^4} + {x^3} – 2{x^2} + 3ax + \dfrac{1}{4}$.
b) Các hệ số có trong đa thức P(x) là: $1; 1; – 2; 3a; \dfrac{1}{4}$.
Tổng các hệ số bằng \(\dfrac{5}{2}\) hay:
$1 + 1 – 2 + 3a + \dfrac{1}{4} = \dfrac{5}{2}\\ \to 3a = \dfrac{9}{4}\\ \to a = \dfrac{3}{4}$
Vậy \(a = \dfrac{3}{4}\).
Giải bài 4 trang 63 Toán 7 tập 2 CD
Từ tấm bìa hình chữ nhật có kích thước 20 cm và 30 cm, bạn Quân cắt đi ở mỗi góc của tấm bìa một hình vuông sao cho bốn hình vuông bị cắt đi có cùng độ dài cạnh, sau đó gấp lại để tạo thành hình hộp chữ nhật không nắp (Hình 5). Viết đa thức biểu diễn thể tích của hình hộp chữ nhật được tạo thành theo độ dài cạnh của hình vuông bị cắt đi.
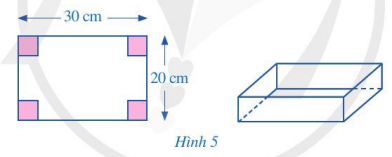
Bài giải:
Gọi độ dài cạnh hình vuông bị cắt đi là x (cm). Vậy chiều cao của hình hộp chữ nhật là x (cm),
Chiều dài tấm bìa sau khi cắt hay chiều dài hình hộp chữ nhật là: \(30 – 2x\) (cm).
Chiều rộng tấm bìa sau khi cắt hay chiều rộng hình hộp chữ nhật là: \(20 – 2x\)(cm).
Thể tích hình hộp chữ nhật là:
$(30 – 2x).(20 – 2x).x \\= (30 – 2x)(20x – 2{x^2})\\ = 30(20x – 2{x^2}) – 2x(20x – 2{x^2})\\ = 600x – 60{x^2} – 40{x^2} + 4{x^3}\\ = 4{x^3} – 100{x^2} + 600x (cm^3)$
Vậy đa thức biểu diễn thể tích của hình hộp chữ nhật được tạo thành theo độ dài cạnh của hình vuông bị cắt đi là \(4{x^3} – 100{x^2} + 600x\).
Giải bài 5 trang 63 Toán 7 tập 2 CD
Ảo thuật với đa thức
Bạn Hạnh bảo với bạn Ngọc:
“– Nếu bạn lấy tuổi của một người bất kì cộng thêm 5;
– Được bao nhiêu đem nhân với 2;
– Lấy kết quả đó cộng với 10;
– Nhân kết quả vừa tìm được với 5;
– Đọc kết quả cuối cùng sau khi trừ đi 100. Mình sẽ đoán được tuổi của người đó.”
Em hãy sử dụng kiến thức nhân đa thức để giải thích vì sao bạn Hạnh lại đoán được tuổi người đó.
Bài giải:
Gọi số tuổi của một người là x (tuổi).
– Nếu bạn lấy tuổi của một người bất kì cộng thêm 5: \(x + 5\)
– Được bao nhiêu đem nhân với 2: \((x + 5).2 = 2x + 10\)
– Lấy kết quả đó cộng với 10: \(2x + 10 + 10 = 2x + 20\)
– Nhân kết quả vừa tìm được với 5: \((2x + 20).5 = 10x + 100\)
– Đọc kết quả cuối cùng sau khi trừ đi 100: \(10x + 100 – 100 = 10x\).
Vậy kết quả cuối cùng mà bạn Ngọc đọc sẽ là \(10x\) tức là 10 lần số tuổi của người đó. Vậy nên khi có kết quả mà bạn Ngọc đọc lên, bạn Hạnh chỉ cần lấy số đó chia cho 10 là ra tuổi của người mà bạn Hạnh chọn.
Bài trước:
👉 Giải bài 1 2 3 4 5 trang 59 sgk Toán 7 tập 2 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 trang 67 sgk Toán 7 tập 2 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 trang 63 sgk Toán 7 tập 2 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
