Nội Dung
Hướng dẫn giải Bài 1. Khái niệm hàm số sgk Toán 8 tập 2 bộ Chân Trời Sáng Tạo. Nội dung bài Giải bài 1 2 3 4 5 trang 9 sgk Toán 8 tập 2 Chân Trời Sáng Tạo bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động khởi động, khám phá, thực hành, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
BÀI 1. KHÁI NIỆM HÀM SỐ
Hoạt động khởi động trang 6 Toán 8 tập 2 CTST
Số liệu về lượng mưa M (mm) trong 7 tháng mùa mưa của thành phố Đà Lạt năm 2020 được biểu diễn theo số n chỉ số trong tháng có biểu đồ dưới đây.
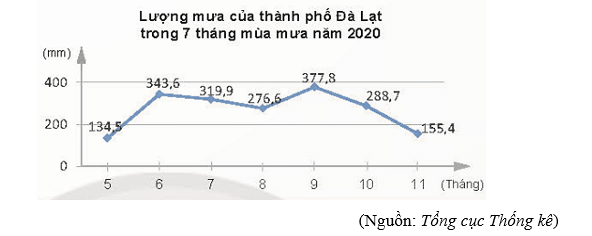
Quan sát biểu đồ và cho biết lượng mưa ở mỗi tháng là bao nhiêu?
Trả lời:
Từ biểu đồ ta thấy:
– Lượng mưa tháng $5$ là $134,5 mm$;
– Lượng mưa tháng $6$ là $343,6 mm$;
– Lượng mưa tháng $7$ là $319,9 mm$;
– Lượng mưa tháng $8$ là $276,6 mm$;
– Lượng mưa tháng $9$ là $377,8 mm$;
– Lượng mưa tháng $10$ là $288,7 mm$;
– Lượng mưa tháng $11$ là $155,4 mm$.
1. KHÁI NIỆM HÀM SỐ
Hoạt động khám phá 1 trang 6 Toán 8 tập 2 CTST
a) Nhiệt độ cơ thể d \((^\circ C)\) của bệnh nhân theo thời gian h (giờ) trong ngày được ghi trong bảng sau:
| $h$ (giờ) | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| $d$ (°C) | 36 | 37 | 36 | 37 | 38 | 37 | 38 | 39 | 39 |
Ứng với mỗi giờ em đọc được bao nhiêu số chỉ nhiệt độ?
b) Thời gian \(t\) (giờ) để một vật chuyển động đều đi hết quãng đường $180$ km tỉ lệ nghịch với vận tốc \(v\) (km/h) của nó theo công thức \(t = \dfrac{{180}}{v}\).
Tính và lập bảng các giá trị tương ứng của \(t\) và \(v\) lần lượt bằng $10; 20; 30; 60; 180$.
Ứng với mỗi giá trị của đại lượng \(v\) em tính được bao nhiêu giá trị của đại lượng \(t\)?
Trả lời:
a) Ứng với mỗi giờ chỉ đọc được một số chỉ nhiệt độ, do đó:
– Ứng với 7h thì nhiệt độ là \(36^\circ C\)
– Ứng với 8h thì nhiệt độ là \(37^\circ C\)
– Ứng với 9h thì nhiệt độ là \(36^\circ C\)
– Ứng với 10h thì nhiệt độ là \(37^\circ C\)
– Ứng với 11h thì nhiệt độ là \(38^\circ C\)
– Ứng với 12h thì nhiệt độ là \(37^\circ C\)
– Ứng với 13h thì nhiệt độ là \(38^\circ C\)
– Ứng với 14h thì nhiệt độ là \(39^\circ C\)
– Ứng với 15h thì nhiệt độ là \(39^\circ C\)
b) Thay $v$ vào \(t = \dfrac{{180}}{v}\) ta được:
– Với \(v = 10 ⇒ t = \dfrac{{180}}{{10}} = 18\)
– Với \(v = 20 ⇒ t = \dfrac{{180}}{{20}} = 9\)
– Với \(v = 30 ⇒ t = \dfrac{{180}}{{30}} = 6\)
– Với \(v = 60 ⇒ t = \dfrac{{180}}{{60}} = 3\)
– Với \(v = 180 ⇒ t = \dfrac{{180}}{{180}} = 1\)
Ta có bảng sau:
| \(v\) | 10 | 20 | 30 | 60 | 180 |
| \(t\) | 18 | 9 | 6 | 3 | 1 |
Thực hành 1 trang 7 Toán 8 tập 2 CTST
Mô tả các đại lượng là hàm số và biến số trong các mô hình sau:
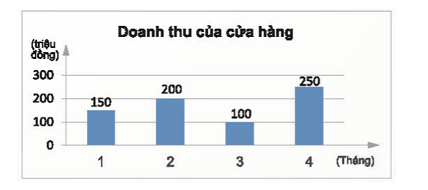
a) Biểu đồ cột chỉ doanh thu \(y\) (triệu đồng) của một cửa hàng trong các tháng \(x\).
b) Quãng đường \(s\) (km) đi được trong khoảng thời gian \(t\) (giờ) của một chiếc xe chạy với tốc độ không đổi bằng $40$ km/h.
c) Số tiền \(y\) (đồng) người mua phải trả cho \(x\) quyển vở có giá trị $10 \,000$ đồng/ quyển.
Trả lời:
a) Đại lượng là hàm số là doanh thu (triệu đồng) của một cửa hàng và biến số là tháng $x$.
b) Đại lượng là hàm số là quãng đường đi được và biến số là thời gian .
c) Đại lượng là hàm số là số tiền người mua phải trả và biến số là số quyển vở.
Vận dụng 1 trang 7 Toán 8 tập 2 CTST
Khi đo nhiệt độ, ta có công thức đổi từ đơn vị độ $C$ (Celsius) sang đơn vị độ $F$ (Fahrenheit) như sau: $F = 1,8C + 3,2$. Theo em, $F$ có phải làm một hàm số theo biến số $C$ hay không? Giải thích.
Trả lời:
$F$ là một hàm số theo biến $C$ vì với mỗi giá trị của $C$ chỉ cho ta duy nhất một giá trị của $F$.
2. GIÁ TRỊ CỦA HÀM SỐ
Hoạt động khám phá 2 trang 7 Toán 8 tập 2 CTST
Cho biết đại lượng \(y\) được tính theo đại lượng \(x\) như sau: \(y = 2x + 3\).
| $x$ | 1 | 2 | 3 | 4 | … |
| $y = 2x + 3$ | 5 | 7 | 9 | … | … |
a) Tính \(y\) khi \(x = 4\).
b) Cho \(x\) một giá trị tùy ý, tính giá trị tương ứng của \(y\).
Trả lời:
a) Với \(x = 4\) ta được. \(y = 2.4 + 3 = 11\)
b) Với \(x = 5\) ta được. \(y = 2.5 + 3 = 13\)
| \(x\) | 1 | 2 | 3 | 4 | 5 |
| \(y = 2x + 3\) | 5 | 7 | 9 | 11 | 13 |
Thực hành 2 trang 8 Toán 8 tập 2 CTST
a) Các giá trị tương ứng của hai đại lượng \(x\) và \(y\) được cho trong bảng sau:
| $x$ | −3 | −2 | −1 | 1 | 2 | 3 |
| $y$ | −6 | −4 | −2 | 2 | 4 | 6 |
Đại lượng \(y\) có phải là hàm số của đại lượng \(x\) không?
b) Cho hàm số \(y = f(x) = {x^2}\)
– Tính \(f(2)); \,f(-3)\).
– Lập bảng giá trị của hàm số với \(x\) lần lượt bằng \( – 3; – 2; – 1;0;1;2;3\).
Trả lời:
a) Đại lượng \(y\) là hàm số của đại lượng \(x\) vì với mỗi giá trị của \(x\) ta chỉ xác nhận được duy nhất một giá trị \(y\) tương ứng.
b) Ta có:
♦ $f(2) = {2^2} = 4$;
♦ $f( – 3) = {( – 3)^2} = 9$
Ta thay nốt các giá trị của $x$ vào hàm số $f(x)$:
♦ $f( – 2) = {( – 2)^2} = 4$
♦ $f( – 1) = {( – 1)^2} = 1$
♦ $f(0) = {0^2} = 0$
♦ $f(1) = {1^2} = 1$
♦ $f(2) = {2^2} = 4$
♦ $f(3) = {3^2} = 9$
Từ đó ta có bảng:
| \(x\) | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| \(f(x)\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Vận dụng 2 trang 8 Toán 8 tập 2 CTST
Cho \(C = f(dt)\) là hàm số mô tả mối quan hệ giữa chu vi \(C\) và đường kính \(d\) của một đường tròn. Tìm công thức \(f(d)\) và lập bảng giá trị của hàm số ứng với \(d\) lần lượt bằng \(1;2;3;4\) (theo đơn vị cm).
Trả lời:
Ta có: \(C = \pi .d\) trong đó, \(C\) là chu vi đường tròn; \(d\) là đường kính và \(\pi \) là số pi.
Do đó, \(f(d) = \pi .d\)
– Với \(d = 1 ⇒ f(1) = \pi .1 = \pi \);
– Với \(d = 2 ⇒ f(2) = \pi .2 = 2\pi \);
– Với \(d = 3 ⇒ f(3) = \pi .3 = 3\pi \);
– Với \(d = 4 ⇒ f(4) = \pi .4 = 4\pi \).
Ta thu được bảng sau:
| \(d\) | 1 | 2 | 3 | 4 |
| \(f(d)\) | \(\pi \) | \(2\pi \) | \(3\pi \) | \(4\pi \) |
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 5 trang 9 sgk Toán 8 tập 2 Chân Trời Sáng Tạo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 9 Toán 8 tập 2 CTST
Các giá trị tương ứng của hai đại lượng \(x\) và \(y\) được cho trong bảng sau. Trong mỗi trường hợp, hãy cho biết đại lượng \(y\) có phải là hàm số của đại lượng \(x\) không? Giải thích.
a)
| $x$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| $y$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
b)
| $x$ | -3 | -2 | -1 | 1 | 2 | 2 |
| $y$ | $-\dfrac{1}{3}$ | $-\dfrac{1}{2}$ | -1 | 1 | $\dfrac{1}{2}$ | $\dfrac{1}{3}$ |
Bài giải:
a) Bảng a): đại lượng \(y\) là hàm số của đại lượng \(x\) vì với mỗi giá trị của \(x\) ta chỉ nhận được duy nhất một giá trị tương ứng của \(y\).
b) Bảng b): đại lượng \(y\) không là hàm số của đại lượng \(x\) vì có những giá trị của \(x\) cho ta hai giá trị \(y\).
Với \(x = 2\) cho ta hai giá trị \(y\) là \(y = \dfrac{1}{2}\) và \(y = \dfrac{1}{3}\).
Giải bài 2 trang 9 Toán 8 tập 2 CTST
Cho hàm số \(y = f(x) = 3x\).
a) Tính \(f(1); \, f(- 2); \, f(\dfrac{1}{3})\).
b) Lập bảng các giá trị tương ứng của \(y\) khi \(x\) lần lượt nhận các giá trị:
\( – 3; – 2; – 1;0;1;2;3\).
Bài giải:
a) Ta có:
♦ $f(1) = 3.1 = 3$;
♦ $f(−2) = 3.(−2) = −6$;
♦ $f(\dfrac{1}{3}) = 3.\dfrac{1}{3} = 1$
b) Ta có:
♦ $f(-3) = 3.(-3) = -9$;
♦ $f(−1) = 3.(−1) = −3$;
♦ $f(0) = 3.0 = 0$
♦ $f(2) = 3.2 = 6$
♦ $f(3) = 3.3 = 9$
Từ đó ta có bảng sau:
| \(x\) | –3 | –2 | –1 | 0 | 1 | 2 | 3 |
| \(y\) | –9 | –6 | –3 | 0 | 3 | 6 | 9 |
Giải bài 3 trang 9 Toán 8 tập 2 CTST
Cho hàm số \(y = f(x) = {x^2} + 4\). Tính \(f(- 3); \,f(- 2); \,f(- 1); \,f(0); \,f(1)\).
Bài giải:
Ta có:
♦ \(f(- 3) = {(- 3)^2} + 4 = 9 + 4 = 13\);
♦ \(f(- 2) = {(- 2)^2} + 4 = 4 + 4 = 8\);
♦ \(f(- 1) = {(- 1)^2} + 4 = 1 + 4 = 5\);
♦ \(f(0) = {0^2} + 4 = 0 + 4 = 4\);
♦ \(f(1) = {1^2} + 4 = 1 + 4 = 5\).
Giải bài 4 trang 9 Toán 8 tập 2 CTST
Khối lượng $m (g)$ của một thanh sắt có khối lượng riêng là $7,8 kg/dm^3$ tỉ lệ thuận với thể tích $V (cm^3)$ theo công thức $m = 7,8V$. Đại lượng $m$ có phải là hàm số của đại lượng $V$ không? Nếu có, tính $m(10); \,m(20); \,m(40); \,m(50)$.
Bài giải:
Đại lượng $m$ là hàm số của đại lượng $V$ vì với mỗi một giá trị của $V$ ta luôn chỉ xác định được một giá trị của $m$.
Ta có: $m = 7,8V$
♦ $m(10) = 7,8.10 = 78$$;
♦ $m(20) = 7,8.20 = 156$;
♦ $m(40) = 7,8.40 = 312$;
♦ $m(50) = 7,8.50 = 390$.
Giải bài 5 trang 9 Toán 8 tập 2 CTST
Thời gian \(t\) (giờ) của một vật chuyển động đều trên quãng đường $20$ km tỉ lệ nghịch với tốc độ \(v\) (km/h) của nó theo công thức \(t = \dfrac{{20}}{v}\). Tính và lập bảng các giá trị tương ứng của \(t\) với \(v\) lần lượt nhận các giá trị $10; 20; 40; 80$.
Bài giải:
Ta có:
♦ Với \(v = 10 ⇒ t(10) = \dfrac{{20}}{{10}} = 2\);
♦ Với \(v = 20 ⇒ t(20) = \dfrac{{20}}{{20}} = 1\);
♦ Với \(v = 40 ⇒ t(40) = \dfrac{{20}}{{40}} = 0,5\);
♦ Với \(v = 80 ⇒ t(80) = \dfrac{{20}}{{80}} = 0,25\).
Khi đó, ta có bảng sau:
| \(v\) | 10 | 20 | 40 | 80 |
| $t$ | 2 | 1 | 0,5 | 0,25 |
Bài trước:
👉 HĐTH&TN: Thiết lập kế hoạch cho một mục tiêu tiết kiệm sgk Toán 8 tập 1 Chân Trời Sáng Tạo
Bài tiếp theo:
👉 Giải bài 1 2 3 4 5 6 7 8 trang 14 sgk Toán 8 tập 2 Chân Trời Sáng Tạo
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 5 trang 9 sgk Toán 8 tập 2 Chân Trời Sáng Tạo đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
