Nội Dung
Hướng dẫn giải Bài §4. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh sgk Toán 7 tập 2 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 trang 83 sgk Toán 7 tập 2 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
§4. TRƯỜNG HỢP BẰNG NHAU THỨ NHẤT CỦA TAM GIÁC: CẠNH – CẠNH – CẠNH
Câu hỏi khởi động trang 80 Toán 7 tập 2 CD
Giá để đồ ở Hình 33 gợi nên hình ảnh hai tam giác ABC và A’B’C’ có: $AB = A’B’, BC = B’C’, CA = C’A’$.
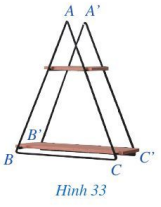
Tam giác ABC có bằng tam giác A’B’C’ hay không?
Trả lời:
Tam giác ABC có bằng tam giác A’B’C’ (vì 2 tam giác này có thể chồng khít lên nhau).
I. TRƯỜNG HỢP BẰNG NHAU CẠNH – CẠNH – CẠNH (c.c.c)
Hoạt động 1 trang 80 Toán 7 tập 2 CD
Cho hai tam giác ABC và A’B’C’ (Hình 34) có: AB = A’B’ = 2 cm, AC = A’C’ = 3 cm, BC = B’C’ = 4 cm. Hãy sử dụng thước đo góc để kiểm nghiệm rằng: \(\widehat A = \widehat {A’}; \widehat B = \widehat {B’}; \widehat C = \widehat {C’}.\)

Trả lời:
Sử dụng thước đo góc ta thấy:
Trong tam giác ABC:
\(\widehat A \approx 105^\circ; \widehat B \approx 45^\circ; \widehat C \approx 29^\circ \).
Trong tam giác A’B’C’:
\(\widehat {A’} \approx 105^\circ; \widehat {B\prime } \approx 45^\circ; \widehat C \approx 29^\circ \).
Vậy \(\widehat A = \widehat {A’}; \widehat B = \widehat {B’}; \widehat C = \widehat {C’}\).
Luyện tập vận dụng trang 81 Toán 7 tập 2 CD
Hai tam giác ở Hình 37 có bằng không? Vì sao?
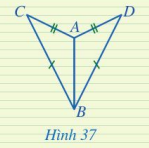
Trả lời:
Xét tam giác ABC và tam giác ABD:
AC = AD; BC = BD, cạnh AB chung.
Vậy \(\Delta ABC = \Delta ABD\) (c.c.c)
II. ÁP DỤNG VÀO TRƯỜNG HỢP BẰNG NHAU VỀ CẠNH HUYỀN VÀ CẠNH GÓC VUÔNG CỦA TAM GIÁC VUÔNG
Hoạt động 2 trang 82 Toán 7 tập 2 CD
Cho hai tam giác vuông ABC và A’B’C’ có: \(\widehat A = \widehat {A’} = 90^\circ, AB = A’B’ = 3\) cm, \(BC = B’C’ = 5\) cm (Hình 39). So sánh độ dài các cạnh AC và A’C’.
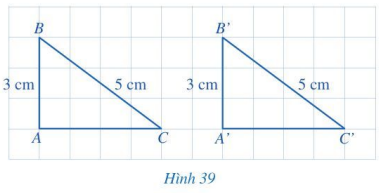
Trả lời:
Ta thấy:
$AC = 4 cm; A’C’ = 4 cm$.
Vậy $AC = A’C’$.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 trang 83 sgk Toán 7 tập 2 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 83 Toán 7 tập 2 CD
Cho Hình 42 có MN = QN, MP = QP. Chứng minh \(\widehat {MNP} = \widehat {QNP}\).
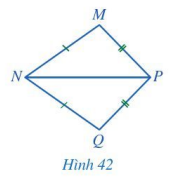
Bài giải:
Xét tam giác MNP và tam giác QNP:
MN = QN; MP = QP; NP chung.
Vậy \(\Delta MNP = \Delta QNP\) (c.c.c)
Vậy \(\widehat {MNP} = \widehat {QNP}\) (2 góc tương ứng).
Giải bài 2 trang 83 Toán 7 tập 2 CD
Cho Hình 43 có AB = AD, \(\widehat {ABC} = \widehat {ADC} = 90^\circ \). Chứng minh \(\widehat {ACB} = \widehat {ACD}\).
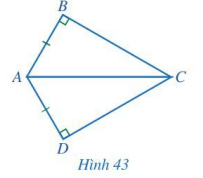
Bài giải:
Xét hai tam giác vuông ABC và ADC có:
AB = AD, AC chung.
Nên \(\Delta ABC = \Delta ADC\) (cạnh huyền – cạnh góc vuông)
⇒ \(\widehat {ACB} = \widehat {ACD}\) (2 góc tương ứng).
Giải bài 3 trang 83 Toán 7 tập 2 CD
Cho Hình 44 có AC = BD, \(\widehat {ABC} = \widehat {BAD} = 90^\circ \). Chứng minh AD = BC.
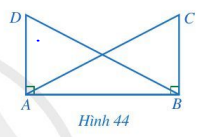
Bài giải:
Xét hai tam giác vuông DAB và CBA:
AC = BD; AB chung.
Nên \(\Delta DAB = \Delta CBA\) (cạnh huyền – cạnh góc vuông)
⇒ $AD = BC$ (2 cạnh tương ứng).
Giải bài 4 trang 83 Toán 7 tập 2 CD
Cho hai tam giác ABC và MNP thỏa mãn: AB = MN, BC = NP, AC = MP, \(\widehat A = 65^\circ ,\widehat N = 71^\circ \). Tính số đo các góc còn lại của hai tam giác.
Bài giải:

Tam giác ABC và tam giác MNP bằng nhau (có ba cặp cạnh bằng nhau: AB = MN, BC = NP, AC = MP). Nên các cặp góc tương ứng trong hai tam giác này bằng nhau:
\(\widehat A = \widehat M, \widehat B = \widehat N, \widehat C = \widehat P\).
Vậy \(\widehat A = \widehat M = 65^\circ \); \(\widehat B = \widehat N = 71^\circ \); \(\widehat C = \widehat P = 180^\circ – 65^\circ – 71^\circ = 44^\circ \) (vì tổng ba góc trong một tam giác bằng 180°).
Bài trước:
👉 Giải bài 1 2 3 4 trang 79 sgk Toán 7 tập 2 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 trang 86 87 sgk Toán 7 tập 2 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 trang 83 sgk Toán 7 tập 2 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
