Nội Dung
Hướng dẫn giải Bài §1. Góc ở vị trí đặc biệt sgk Toán 7 tập 1 bộ Cánh Diều. Nội dung bài Giải bài 1 2 3 4 trang 94 95 sgk Toán 7 tập 1 Cánh Diều bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
§1. GÓC Ở VỊ TRÍ ĐẶC BIỆT
Câu hỏi khởi động trang 90 Toán 7 tập 1 CD
Trên mặt đồng hồ ở Hình 1, quan sát hai góc; góc tạo bởi kim giờ và kim phút; góc tạo bởi kim phút và kim giây.

Hai góc đó có liên hệ gì đặc biệt?
Trả lời:
Trong Hình 1, góc tạo bởi kim giờ và kim phút; góc tạo bởi kim phút và kim giây là hai góc có điểm gốc chung và có một cạnh chung là kim phút.
Hoặc:
2 góc được đánh dấu là 2 góc có: chung đỉnh; có chung một cạnh ; kim giờ và kim giây nằm về hai phía của kim phút.
I. HAI GÓC KỀ NHAU
Hoạt động 1 trang 90 Toán 7 tập 1 CD
Cho đường thẳng xy. Từ một điểm O trên đường thẳng xy ta vẽ hai tia Oz, Ot như Hình 2.
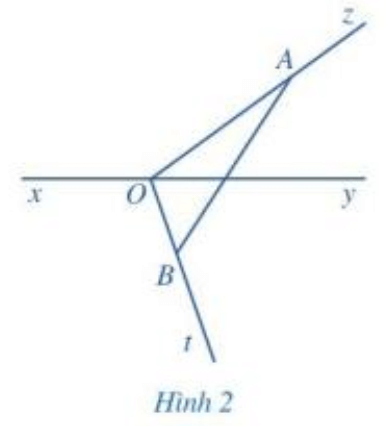
a) Lấy điểm A bất kì trên tia Oz (A khác O), lấy điểm B bất kì trên tia Ot (B khác O), vẽ đoạn thẳng AB.
b) Đoạn thẳng AB có cắt đường thẳng xy hay không?
Trả lời:
a) Thực hiện vẽ hình theo các bước như đề bài ta được hình vẽ.
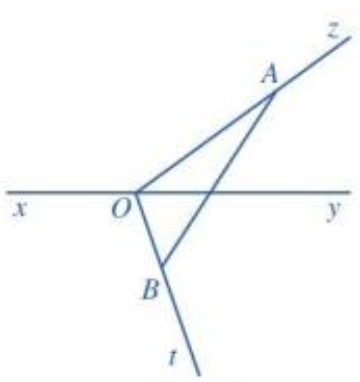
b) Đoạn thẳng AB cắt đường thẳng xy
Hoạt động 2 trang 90 Toán 7 tập 1 CD
Quan sát hai góc xOy và zOy ở Hình 3.
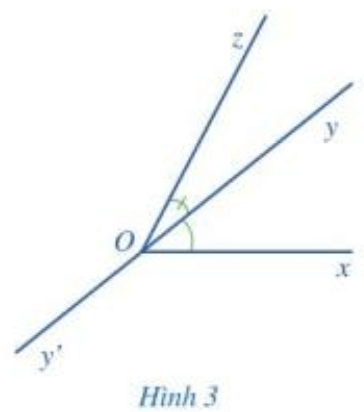
a) Nêu đỉnh chung và cạnh chung của hai góc xOy và zOy.
b) Vẽ tia đối Oy’ của tia Oy.
c) Hai tia Ox và Oz có nằm về hai phía của đường thẳng yy’ hay không?
Trả lời:
a) Hai góc xOy và zOy có đỉnh O chung và cạnh Oy chung.
b) Vẽ tia đối Oy’ của tia Oy:
– Đặt thước thẳng sao cho mép thước trùng với tia Oy.
– Vẽ tia Oy’ sao cho hai tia Oy và Oy’ cùng nằm trên đường thẳng; chữ cái y và y’ được viết vào hai phía của O và sát vào đường thẳng vừa vẽ.
Khi đó, hai tia Oy’ là tia đối của tia Oy (như hình vẽ).
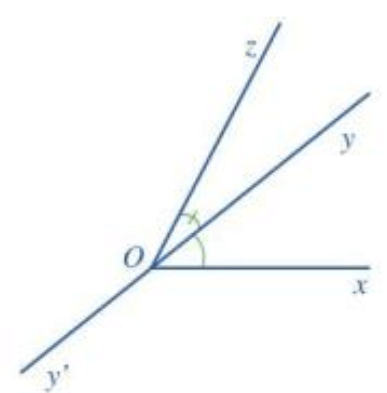
c) Hai tia Ox và Oz nằm về hai phía của đường thẳng yy’.
Luyện tập vận dụng 1 trang 91 Toán 7 tập 1 CD
Ở Hình 6, hai góc xOy và mOn có phải là hai góc kề nhau hay không? Vì sao?
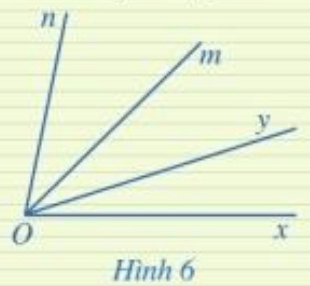
Trả lời:
Ta thấy: Hai góc xOy và mOn có đỉnh O chung nhưng không có cạnh chung. Do đó, hai góc xOy và mOn không phải là hai góc kề nhau
Luyện tập vận dụng 2 trang 92 Toán 7 tập 1 CD
Ở Hình 9, hai góc mOn và pOn có là hai góc kề nhau hay không? Tính số đo của góc mOp.
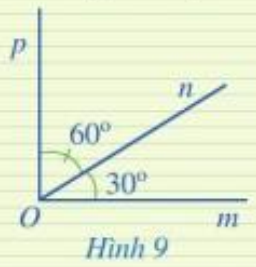
Trả lời:
Hai góc mOn và pOn có là hai góc kề nhau vì có đỉnh O chung, cạnh On chung, 2 cạnh còn lại là Om và Op nằm về hai phía so với đường thẳng chứa On.
Vì On nằm trong góc mOp nên
\(\begin{array}{l}\widehat {mOn} + \widehat {nOp} = \widehat {mOp} \Rightarrow 30^\circ + 60^\circ = \widehat {mOp}\\ \Rightarrow 90^\circ = \widehat {mOp}\end{array}\)
Vậy \(\widehat {mOp} = 90^\circ \)
II. HAI GÓC BÙ NHAU. HAI GÓC KỀ BÙ
Hoạt động 3 trang 92 Toán 7 tập 1 CD
Tìm tổng số đo của góc 110o và góc 70o.
Trả lời:
Tổng số đo của góc 110° và góc 70° là:
110° + 70° = 180°.
Vậy tổng số đo của hai góc đã cho là 180°.
Hoạt động 4 trang 92 Toán 7 tập 1 CD
Quan sát hai góc xOt và yOt ở Hình 10, trong đó Ox và Oy là hai tia đối nhau.
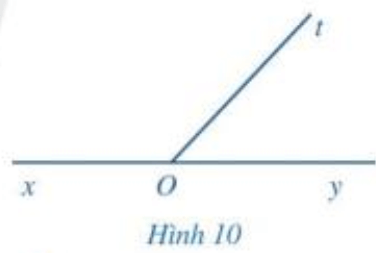
a) Hai góc xOt và yOt có kề nhau hay không?
b) Tính \(\widehat {xOt} + \widehat {yOt}\)
Trả lời:
a) Hai góc xOt và yOt là hai góc kề nhau vì có đỉnh O chung, cạnh Ot chung, 2 cạnh còn lại là Ox và Oy nằm về hai phía so với đường thẳng chứa tia Ot
b) Vì tia Ot nằm trong góc xOy nên \(\widehat {xOt} + \widehat {yOt} = \widehat {xOy}\)
Mà \(\widehat {xOy} = 180^\circ \) ( góc bẹt)
\( \Rightarrow \widehat {xOt} + \widehat {yOt} = 180^\circ \)
Chú ý: Ta có thể đo số đo 2 góc xOt và yOt rồi tính tổng của chúng.
Luyện tập vận dụng 3 trang 93 Toán 7 tập 1 CD
Tính góc xOt trong Hình 12.
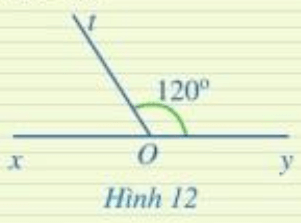
Trả lời:
Hai góc xOt và yOt có chung đỉnh O, chung cạnh Ot và hai cạnh Ox và Oy nằm về hai phía của tia Ot.
Ta có: \(\widehat {xOt} + \widehat {tOy} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {xOt} + 120^\circ = 180^\circ \\ \Rightarrow \widehat {xOt} = 180^\circ – 120^\circ = 60^\circ \end{array}\)
III. HAI GÓC ĐỐI ĐỈNH
Hoạt động 5 trang 93 Toán 7 tập 1 CD
Quan sát hai góc xOz và yOt ở Hình 13, trong đó Ox và Oy là hai tia đối nhau, Oz và Ot cũng là hai tia đối nhau và cho biết:

a) Cạnh Ox của góc xOz là tia đối của cạnh nào của góc yOt.
b) Cạnh Oz của góc xOz là tia đối của cạnh nào của góc yOt.
Trả lời:
a) Cạnh Ox của góc xOz là tia đối của cạnh Oy của góc yOt.
b) Cạnh Oz của góc xOz là tia đối của cạnh Ot của góc yOt.
Hoạt động 6 trang 94 Toán 7 tập 1 CD
Quan sát Hình 15 và giải thích vì sao:
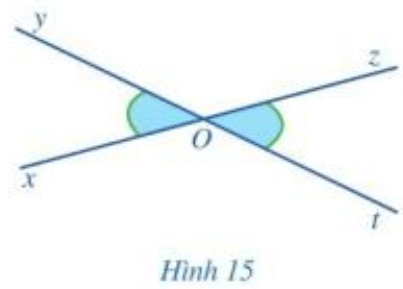
a) Hai góc xOy và yOz là hai góc kề bù;
b) Hai góc yOz và zOt là hai góc kề bù;
c) \(\widehat {xOy} + \widehat {yOz} = \widehat {yOz} + \widehat {zOt}\) và \(\widehat {xOy} = \widehat {zOt}\)
Trả lời:
a) Vì 2 góc có chung gốc O, chung cạnh Oy, 2 cạnh còn lại là Ox và Oz nằm về hai phía đối với đường thẳng chứa tia Oy nên hai góc xOy và yOz là hai góc kề nhau. Hơn nữa, hai góc xOy và yOz có tổng bằng góc xOz =180 độ nên hai góc xOy và yOz là hai góc bù nhau.
Vậy hai góc xOy và yOz là hai góc kề bù.
b) Vì 2 góc có chung gốc O, chung cạnh Oz, 2 cạnh còn lại là Oy và Ot nằm về hai phía đối với đường thẳng chứa tia Oz nên hai góc yOz và zOt là hai góc kề nhau. Hơn nữa, hai góc yOz và zOt có tổng bằng góc xOz =180 độ nên hai góc yOz và zOt là hai góc bù nhau.
Vậy hai góc yOz và zOt là hai góc kề bù
c) Do $\widehat {xOy} + \widehat {yOz} = \widehat {xOz} = 180^\circ $
và $\widehat {yOz} + \widehat {zOt} = \widehat {yOt} = 180^\circ$
Vậy \(\widehat {xOy} + \widehat {yOz} = \widehat {yOz} + \widehat {zOt}\)
\( \Rightarrow \widehat {xOy} = \widehat {zOt}\)
Chú ý: Ta có thể dùng dấu hiệu sau: 2 góc kề bù khi có chung đỉnh, chung một cạnh, 2 cạnh còn lại là 2 tia đối nhau.
Luyện tập vận dụng 4 trang 94 Toán 7 tập 1 CD
Tìm số đo x trong Hình 17.
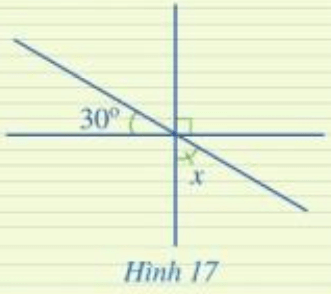
Trả lời:
Đặt tên các góc như hình vẽ:
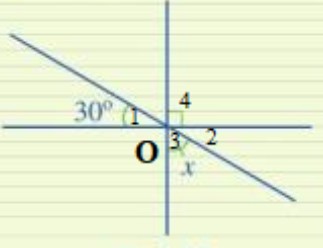
Ta có: \(\widehat {{O_1}} = \widehat {{O_2}}\) (2 góc đối đỉnh). Mà \(\widehat {{O_1}} = 30^\circ \Rightarrow \widehat {{O_2}} = 30^\circ \)
Ta có: \(\widehat {{O_2}} + \widehat {{O_3}} + \widehat {{O_4}} = 180^\circ \) (kề bù)
\(\begin{array}{l} \Rightarrow x + 30^\circ + 90^\circ = 180^\circ \\ \Rightarrow x = 180^\circ – 30^\circ – 90^\circ = 60^\circ \end{array}\)
Vậy x = 60\(^\circ \)
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 4 trang 94 95 sgk Toán 7 tập 1 Cánh Diều. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 94 Toán 7 tập 1 CD
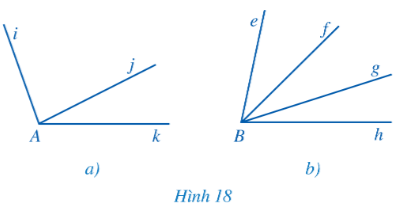
a) Tìm các cặp góc kề nhau trong mỗi hình 18a, 18b:
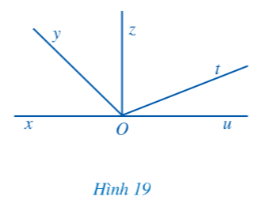
b) Tìm các cặp góc kề bù (khác góc bẹt) ở Hình 19.
c) Tìm hai góc đối đỉnh (khác góc bẹt và góc không) trong mỗi hình 20a, 20b, 20c, 20d:
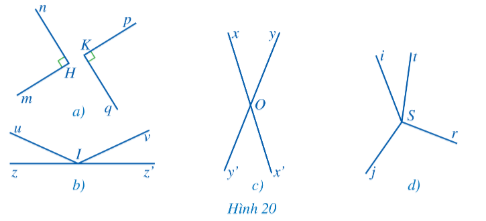
Bài giải:
a) – Xét hình 18a:
Hai góc iAj và jAk có chung đỉnh A, chung cạnh Aj và hai cạnh Ai và Ak nằm về hai phía của tia Aj. Do đó, hai góc iAj và jAk kề nhau.
– Xét hình 18b:
+ Hai góc hBg và gBf có chung đỉnh B, chung cạnh Bg và hai cạnh Bh và Bf nằm về hai phía của tia Bg. Do đó, hai góc hBg và gBf kề nhau.
+ Hai góc gBf và eBf có chung đỉnh B, chung cạnh Bf và hai cạnh Bg và Be nằm về hai phía của tia Bf. Do đó, hai góc gBf và eBf kề nhau.
+ Hai góc hBg và gBe có chung đỉnh B, chung cạnh Bg và hai cạnh Bh và Be nằm về hai phía của tia Bg. Do đó, hai góc hBg và gBe kề nhau.
+ Hai góc eBf và hBf có chung đỉnh B, chung cạnh Bf và hai cạnh Be và Bh nằm về hai phía của tia Bf. Do đó, hai góc eBf và hBf kề nhau.
Vậy trong hình 18a: hai góc iAj và jAk kề nhau;
Trong hình 18b: hai góc hBg và gBf kề nhau; hai góc gBf và eBf kề nhau; hai góc hBg và gBe kề nhau; hai góc eBf và hBf kề nhau.
b) 2 góc kề bù trong Hình 19 là: góc xOy và góc yOu; góc xOz và góc zOu; góc xOt và góc tOu.
c) 2 góc đối đỉnh:
Trong Hình 20a: Không có vì 2 góc này không có chung đỉnh.
Trong Hình 20b: Không có vì không có 2 góc nào mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Trong Hình 20c: góc xOy và góc x’Oy’.
Trong Hình 20d: Không có vì không có 2 góc nào mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.
Giải bài 2 trang 95 Toán 7 tập 1 CD
Quan sát Hình 21 và chỉ ra:
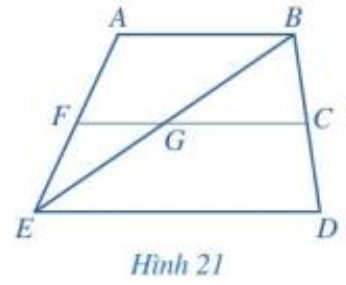
a) Hai góc kề nhau;
b) Hai góc kề bù (khác góc bẹt);
c) Hai góc đối đỉnh (khác góc bẹt và góc không).
Bài giải:
a) 2 góc kề nhau là: góc ABE và EBD; góc AFG và GFE; góc AEB và BED; góc BCG và GCD; góc FGB và BGC; góc BGC và CGE; góc CGE và EGF; góc EGF và FGB.
b) 2 góc kề bù là: góc AFG và GFE; góc BCG và GCD; góc FGB và BGC; góc BGC và CGE; góc CGE và EGF; góc EGF và FGB.
c) 2 góc đối đỉnh là: góc FGB và CGE; góc BGC và EGF
Giải bài 3 trang 95 Toán 7 tập 1 CD
Tìm số đo:
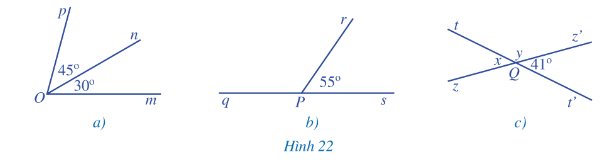
a) Góc mOp trong Hình 22a;
b) Góc qPr trong Hình 22b;
c) x, y trong Hình 22c.
Bài giải:
a) Vì tia On nằm trong góc mOp nên \(\widehat {mOn} + \widehat {nOp} = \widehat {mOp}\)
\(\begin{array}{l} \Rightarrow 30^\circ + 45^\circ = \widehat {mOp}\\ \Rightarrow 75^\circ = \widehat {mOp}\end{array}\)
Vậy số đo góc mOp là 75 độ
b) Ta có: \(\widehat {q\Pr } + \widehat {rPs} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {q\Pr } + 55^\circ = 180^\circ \\ \Rightarrow \widehat {q\Pr } = 180^\circ – 55^\circ = 125^\circ \end{array}\)
Vậy số đo góc qPr là 125 độ
c) Ta có:
\(\widehat {tQz} = \widehat {t’Qz’}\) (2 góc đối đỉnh), mà \(\widehat {t’Qz’} = 41^\circ \Rightarrow \widehat {tQz} = 41^\circ \)
\(\widehat {tQz’} + \widehat {z’Qt’} = 180^\circ \) (2 góc kề bù) nên:
\(\widehat {tQz’} + 41^\circ = 180^\circ \Rightarrow \widehat {tQz’} = 180^\circ – 41^\circ = 139^\circ \)
Vậy x = 41 \(^\circ \) ; y = 139 \(^\circ \).
Giải bài 4 trang 95 Toán 7 tập 1 CD
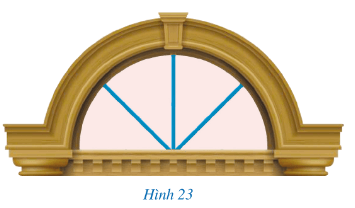
Hình 23 là một mẫu cửa có vòm tròn của một ngôi nhà. Nếu coi mỗi thanh chắn vòm cửa đó như một cạnh của góc thì các thanh chắn đó (ba thanh màu xanh trên hình) như một cạnh của góc thì các thanh chắn đó tạo ra các góc kề nhau. Theo em, mỗi góc tạo bởi hai thanh chắn vòm cửa đó khoảng bao nhiêu độ?
Bài giải:
Trong Hình 23, coi mỗi thanh chắn vòm cửa đó như một cạnh của góc thì các thanh chắn đó tạo ra các góc kề nhau.
Các góc tạo bởi các thanh chắn cửa kề nhau tạo thành một góc bẹt và các góc có số đo gần bằng nhau.
Do đó, số đo mỗi góc bằng khoảng: 180o : 4 = 45o.
Vậy mỗi góc tạo bởi hai thanh chắn vòm cửa đó khoảng 45 độ.
Bài trước:
👉 HĐTH&TN: Chủ đề 2. Tạo đồ dùng dạng hình lăng trụ đứng sgk Toán 7 tập 1 Cánh Diều
Bài tiếp theo:
👉 Giải bài 1 2 3 4 trang 98 99 sgk Toán 7 tập 1 Cánh Diều
Trên đây là bài Hướng dẫn Giải bài 1 2 3 4 trang 94 95 sgk Toán 7 tập 1 Cánh Diều đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
