Nội Dung
Hướng dẫn giải Bài 2. Xác suất thực nghiệm sgk Toán 6 tập 2 bộ Chân Trời Sáng Tạo. Nội dung bài Giải bài 1 2 3 trang 105 sgk Toán 6 tập 2 Chân Trời Sáng Tạo bao gồm đầy đủ câu trả lời các câu hỏi hoạt động khởi động, khám phá, thực hành, vận dụng và bài giải các bài tập, giúp các bạn học sinh học tốt môn toán 6.
Bài 2 Xác suất thực nghiệm
Hoạt động khởi động trang 103 Toán 6 tập 2 CTST

Trả lời:
Trong lần gặp nhau thứ 51 thì người có khả năng giành chiến thắng cao hơn là An.
1. Khả năng xảy ra của một sự kiện
Hoạt động khám phá 1 trang 103 Toán 6 tập 2 CTST
Trong hộp có 5 quả bóng xanh và 1 quả bóng đỏ. Không nhìn vào hộp, chọn ra từ hộp một quả bóng. Xét các sự kiện sau:
– Bóng chọn ra có màu vàng;
– Bóng chọn ra không có màu vàng.
– Bóng chọn ra có màu xanh.
Sự kiện nào có khả năng xảy ra cao nhất?
Trả lời:
– Sự kiện “Bóng chọn ra có màu vàng” không thể xảy ra. Vì trong hộp không có quả bóng màu vàng.
– Sự kiện “Bóng chọn ra không có màu vàng:” chắc chắn xảy ra. Vì trong hộp không có quả bóng màu vàng.
– Trong hộp có cả quả bóng màu xanh và màu đỏ. Khi lấy ra một quả bóng từ trong hộp ra thì có thể lấy được số quả bóng màu xanh hoặc màu đỏ.
Do đó, sự kiện “Bóng chọn ra có màu xanh” có thể xảy ra.
Vậy sự kiện có khả năng xảy ra cao nhất là: “Bóng chọn ra không có màu vàng”.
2. Xác suất thực nghiệm
Hoạt động khám phá 2 trang 103 Toán 6 tập 2 CTST
Thực hiện việc xoay ghim 20 lần quanh trục bút chì và sử dụng bảng kiểm đếm theo mẫu như hình vẽ để đếm số lần ghim chỉ vào mỗi màu.
Hãy tính tỉ số của số lần ghim chỉ vào ô màu trắng và tổng số lần xoay ghim.
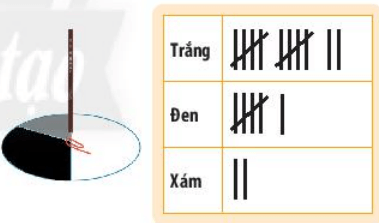
Trả lời:
Tổng số lần xoay ghim là 20 lần.
Số ghim chỉ vào ô màu trắng trong 20 lần xoay là 12 lần.
Tỉ số của số lần ghim chỉ vào ô màu trắng và tổng số lần xoay là:
\(12:20=\frac{12}{20}=\frac{3}{5}\)
Vậy tỉ số của số lần ghim chỉ vào ô màu trắng và tổng số lần xoay là \(\frac{3}{5}\).
Thực hành trang 103 Toán 6 tập 2 CTST
Tìm xác suất thực nghiệm của sự kiện ghim chỉ vào ô màu xám, màu đen.
Trả lời:
Tổng số lần xoay ghim là 20 lần.
Số ghim chỉ vào ô màu xám trong 20 lần xoay là 2 lần.
Xác suất thực nghiệm của sự kiện ghim chỉ vào ô màu xám là:
\(2:20=\frac{2}{20}=\frac{1}{10}\)
Số ghim chỉ vào ô màu đen trong 20 lần xoay là 6 lần.
Xác suất thực nghiệm của sự kiện ghim chỉ vào ô màu đen là:
\(6:20=\frac{6}{20}=\frac{3}{10}\)
Vậy xác suất thực nghiệm của sự kiện ghim chỉ vào ô màu xám là $\frac{1}{10}$.
Và xác suất thực nghiệm của sự kiện ghim chỉ vào ô màu đen là: $\frac{3}{10}$.
Vận dụng trang 104 Toán 6 tập 2 CTST
Hằng ngày Sơn đều đi xe buýt đến trường. Sơn ghi lại thời gian chờ xe của mình trong 20 lần liên tiếp ở bảng sau:

Hãy tính xác suất thực nghiệm của các sự kiện:
a) Sơn phải chờ xe dưới 1 phút.
b) Sơn phải chờ xe từ 5 phút trở lên.
Trả lời:
Tổng số lần Sơn chờ xe buýt là:
$4 + 10 + 4 + 2 = 20$ (lần)
a) Số lần Sơn phải chờ xe dưới 1 phút là 4 (lần).
Xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 1 phút” là:
\(4:20=\frac{4}{20}=\frac{1}{5}\)
Vậy xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 1 phút” là $\frac{1}{5}$.
b) Số lần Sơn phải chờ xe từ 5 phút trở lên là tổng số lần Sơn chờ xe từ 5 phút đến 10 phút và từ 10 phút trở lên.
Do đó, số lần Sơn phải chờ xe từ 5 phút trở lên là:
$4 + 2 = 6$ (lần)
Xác suất thực nghiệm của sự kiện “Sơn phải chờ xe từ 5 phút trở lên” là:
\(6:20=\frac{6}{20}=\frac{3}{10}\)
Vậy xác suất thực nghiệm của sự kiện “Sơn phải chờ xe từ 5 phút trở lên” là $\frac{3}{10}$.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 1 2 3 trang 105 sgk Toán 6 tập 2 Chân Trời Sáng Tạo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 105 Toán 6 tập 2 CTST
Gieo một con xúc xắc 4 mặt 50 lần và quan sát số ghi trên đỉnh của con xúc xắc, ta được kết quả như sau:

Hãy tính xác suất thực nghiệm để:
a) Gieo được đỉnh số 4.
b) Gieo được đỉnh có số chẵn.
Bài giải:
a) Số lần gieo được đỉnh số 4 trong 50 lần gieo là: $9$ (lần).
Vậy xác suất thực nghiệm để “Gieo được đỉnh số 4” là: \(9:50 = \frac{9}{50}\).
b) Các đỉnh là số chẵn trong bảng trên là đỉnh số 2 và số 4.
Số lần gieo được đỉnh số 2 là 14 lần.
Số lần gieo được đỉnh số 4 là 9 lần.
Do đó, số lần gieo được đỉnh có số chẵn là $14 + 9 = 23$ (lần).
Vậy xác suất thực nghiệm để “Gieo được đỉnh có số chẵn” là: $23 : 50 = \frac{23}{50}$.
Giải bài 2 trang 105 Toán 6 tập 2 CTST
Trong hộp có một số bút xanh và một số bút đỏ. Lấy ngẫu nhiên 1 bút từ hộp, xem màu rồi trả lại. Lặp lại hoạt động trên 50 lần, ta được kết quả như sau:

a) Tính xác suất thực nghiệm của sự kiện lấy được bắt xanh.
b) Em hãy dự đoán xem trong hộp loại bút nào có nhiều hơn.
Bài giải:
a) Số lần lấy được bút xanh trong 50 lần trên là: $42$ (lần).
Xác suất thực nghiệm của sự kiện lấy được bút xanh là:
$42 : 50 = \frac{42}{50}$
Vậy xác suất thực nghiệm của sự kiện lấy được bút xanh là $\frac{42}{50}$.
b) Do ta lấy ngẫu nhiên được số bút xanh nhiều hơn số bút đỏ nên có thể dự đoán là trong hộp loại bút xanh có nhiều hơn số bút đỏ.
Giải bài 3 trang 105 Toán 6 tập 2 CTST
Tổng hợp kết quả xét nghiệm bệnh viêm gan ở một phòng khám trong một năm ta được bảng sau:

Hãy tính xác suất thực nghiệm của sự kiện một ca xét nghiệm có kết quả dương tính
a) theo từng quý trong năm.
b) sau lần lượt từng quý tính từ đầu năm.
Bài giải:
a) Xác suất thực hiện một ca xét nghiệm có kết quả dương tính theo từng quý là:
Quý I: \(15:150 = \frac{1}{10}\)
Quý II: \(21:200 = \frac{21}{200}\)
Quý III: \(17:180 = \frac{17}{180}\)
Quý IV: \(24:220 = \frac{6}{55}\)
b) Xác suất thực hiện một ca xét nghiệm có kết quả dương tính sau lần lượt từng quý tính từ đầu năm là:
Quý I: \(15:150 = \frac{1}{{10}}\)
Quý II: \((15+21):(150+200) = \frac{36}{350} = \frac{18}{175}\)
Quý III: \((15+21+17):(150+200+180) = \frac{53}{530} = \frac{1}{10}\)
Quý IV: \((15+21+17+24):(150+200+180+220) = \frac{77}{750}\)
Bài trước:
👉 Giải bài 1 2 3 4 trang 102 sgk Toán 6 tập 2 Chân Trời Sáng Tạo
Bài tiếp theo:
👉 HĐTH&TN: Xác suất thực nghiệm trong trò chơi may rủi sgk Toán 6 tập 2 Chân Trời Sáng Tạo
Trên đây là bài Hướng dẫn Giải bài 1 2 3 trang 105 sgk Toán 6 tập 2 Chân Trời Sáng Tạo đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 6 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
