Giải bài 12 13 14 15 16 17 trang 14 15 sgk Toán 7 tập 1 Kết Nối Tri Thức

Nội Dung

Hướng dẫn giải Bài Luyện tập chung trang 14 sgk Toán 7 tập 1 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 12 13 14 15 16 17 trang 14 15 sgk Toán 7 tập 1 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.

GIẢI BÀI TẬP LUYỆN TẬP CHUNG

Sau đây là phần Giải bài 12 13 14 15 16 17 trang 14 15 sgk Toán 7 tập 1 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1.12 trang 14 Toán 7 tập 1 KNTT

So sánh:

a) $\frac{{123}}{7}$ và $17,75$;

b) $ – \frac{{65}}{9}$ và $-7,125$.

Bài giải:

a) Ta có:

$\frac{{123}}{7} = \frac{{123.4}}{{7.4}} = \frac{{492}}{{28}}\\17,75 = \frac{{1775}}{{100}} = \frac{{71}}{4} = \frac{{71.7}}{{4.7}} = \frac{{497}}{{28}}$

Vì $492 < 497$ nên $\frac{{492}}{{28}} < \frac{{497}}{{28}}$ hay $\frac{{123}}{7} < 17,75$

b) Ta có:

$- \frac{{65}}{9} = \frac{{( – 65).8}}{{9.8}} = \frac{{ – 520}}{{72}}\\ – 7,125 = \frac{{ – 7125}}{{1000}} = \frac{{ – 57}}{8} = \frac{{ – 57.9}}{{8.9}} = \frac{{ – 513}}{{72}}$

Vì $520 > 513$ nên $-520 < -513$. Do đó $\frac{{ – 520}}{{72}} < \frac{{ – 513}}{{72}}$ hay $ – \frac{{65}}{9} < -7,125$.

Giải bài 1.13 trang 15 Toán 7 tập 1 KNTT

Bảng sau cho biết các điểm đông đặc và điểm sôi của sáu nguyên tố được gọi là khí hiếm.

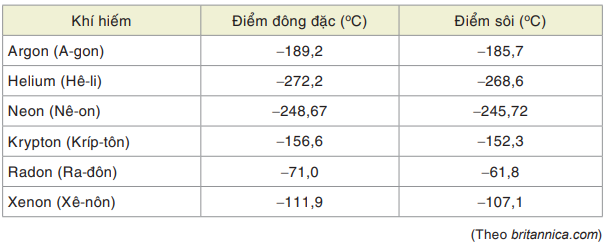
a) Khí hiếm nào có điểm đông đặc nhỏ hơn điểm đông đặc của Krypton?

b) Khí hiếm nào có điểm sôi lớn hơn điểm sôi của Argon?

c) Hãy sắp xếp các khí hiếm theo thứ tự điểm đông đặc tăng dần;

d) Hãy sắp xếp các khí hiếm theo thứ tự điểm sôi giảm dần.

Bài giải:

a) Điểm đông đặc của Krypton là: -156,6 $^\circ $C

Vì $-272,2 < -248,67 < -189,2 < -156,6$ nên các khí hiếm có điểm đông đặc nhỏ hơn điểm đông đặc của Krypton là: Argon, Neon, Helium.

b) Điểm sôi của Argon là: -185,7 $^\circ $C

Vì $-61,8 > -107,1 > -152,3 > -185,7$ nên các khí hiếm nào có điểm sôi lớn hơn điểm sôi của Argon là: Radon, Xenon, Krypton.

c) Vì $-272,2 < -248,67 < -189,2 < -156,6 < -111,9 < -71,0$.

Các khí hiếm theo thứ tự điểm đông đặc tăng dần là: Helium, Neon, Argon, Krypton, Xenon, Radon.

d) Vì $-61,8 > -107,1 > -152,3 > -185,7 > -245,72 > -268,6$.

Các khí hiếm theo thứ tự điểm sôi giảm dần là: Radon, Xenon, Krypton, Argon, Neon, Helium.

Giải bài 1.14 trang 15 Toán 7 tập 1 KNTT

Theo đài khí tượng thủy văn tỉnh Lào Cai, ngày 10-01-2021, nhiệt độ thấp nhất tại thị xã Sa Pa là -0,7$^\circ $C; nhiệt độ tại thành phố Lào Cai khoảng 9,6 $^\circ $C. Hỏi nhiệt độ tại thành phố Lào Cai cao hơn nhiệt độ tại thị xã Sa Pa bao nhiêu độ C?

Bài giải:

Nhiệt độ tại thành phố Lào Cai cao hơn nhiệt độ tại thị xã Sa Pa là:

9,6 – (– 0,7) = 9,6 + 0,7 = 10,3 (^oC).

Vậy nhiệt độ tại thành phố Lào Cai cao hơn 10,3 ^oC so với nhiệt độ tại thị xã Sa Pa.

Giải bài 1.15 trang 15 Toán 7 tập 1 KNTT

Thay mỗi dấu “?” bằng số thích hợp để hoàn thiện sơ đồ Hình 1.11, biết số trong mỗi ô ở hàng trên bằng tích của hai số trong hai ô kề nó ở hàng dưới.

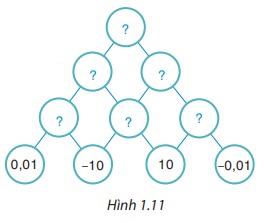
Bài giải:

Đặt các ô lần lượt là a, b, c, d, e, f như hình sau:

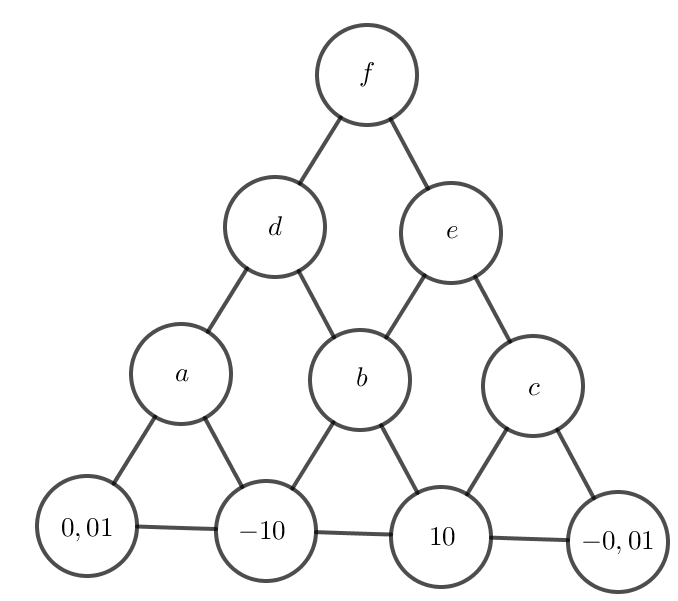
Theo quy luật bài cho, ta được:

$a = 0,01 . (-10) = -0,1$

$b = (-10) . 10 = -100$

$c = 10 . (-0,01) = -0,1$

$d = a.b = (-0,1) . (-100) = 10$

$e = b.c = (-100) . (-0,1) = 10$

$f = d.e = 10 . 10 = 100$

Khi đó ta có bảng sau:

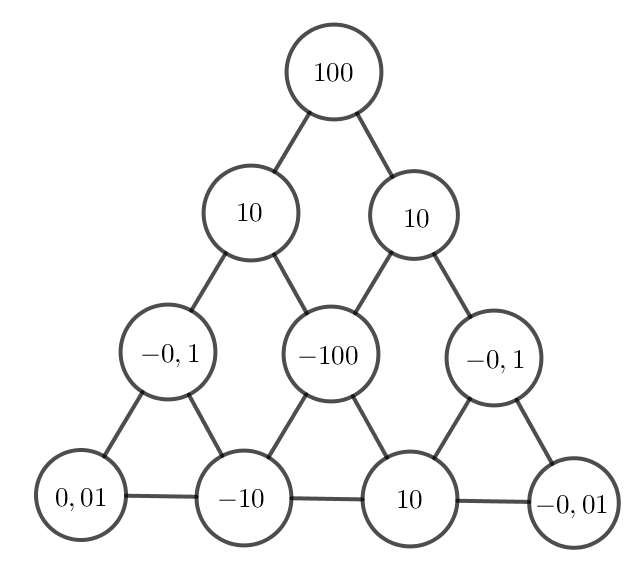
Giải bài 1.16 trang 15 Toán 7 tập 1 KNTT

Tính giá trị của các biểu thức sau:

a) $A = (2 – \frac{1}{2} – \frac{1}{8}):(1 – \frac{3}{2} – \frac{3}{4})$;

b) $B = 5 – \frac{{1 + \frac{1}{3}}}{{1 – \frac{1}{3}}}$.

Bài giải:

a) Ta có:

$A = (2 – \frac{1}{2} – \frac{1}{8}):(1 – \frac{3}{2} – \frac{3}{4})\\ = (\frac{{16}}{8} – \frac{4}{8} – \frac{1}{8}):(\frac{4}{4} – \frac{6}{4} – \frac{3}{4})\\ = \frac{{11}}{8}:\frac{{ – 5}}{4}\\ = \frac{{11}}{8}.\frac{4}{{ – 5}}\\ = \frac{{ – 11}}{{10}}$

b) Ta có:

$B = 5 – \frac{{1 + \frac{1}{3}}}{{1 – \frac{1}{3}}}\\ = 5 – \frac{{\frac{3}{3} + \frac{1}{3}}}{{\frac{3}{3} – \frac{1}{3}}}\\ = 5 – \frac{{\frac{4}{3}}}{{\frac{2}{3}}}\\ = 5 – \frac{4}{3}:\frac{2}{3}\\ = 5 – \frac{4}{3}.\frac{3}{2}\\ = 5 – 2\\ = 3$

Chú ý: Khi thực hiện phép cộng hai phân số, nếu phân số thu được chưa tối giản thì ta rút gọn thành phân số tối giản.

Giải bài 1.17 trang 15 Toán 7 tập 1 KNTT

Tính một cách hợp lí:

$1,2.\frac{{15}}{4} + \frac{{16}}{7}.\frac{{ – 85}}{8} – 1,2.5\frac{3}{4} – \frac{{16}}{7}.\frac{{ – 71}}{8}$

Bài giải:

Ta có thể tính như sau:

$1,2.\frac{{15}}{4} + \frac{{16}}{7}.\frac{{ – 85}}{8} – 1,2.5\frac{3}{4} – \frac{{16}}{7}.\frac{{ – 71}}{8}\\ =(1,2.\frac{{15}}{4} – 1,2.5\frac{3}{4}) +( \frac{{16}}{7}.\frac{{ – 85}}{8}- \frac{{16}}{7}.\frac{{ – 71}}{8}) \\= \frac{{12}}{{10}}.\frac{{15}}{4} – \frac{{12}}{{10}}.\frac{{23}}{4} + \frac{{16}}{7}.\frac{{ – 85}}{8} – \frac{{16}}{7}.\frac{{ – 71}}{8}\\ = \frac{6}{5}.\frac{{15}}{4} – \frac{6}{5}.\frac{{23}}{4} + \frac{{16}}{7}.\frac{{ – 85}}{8} + \frac{{16}}{7}.\frac{{71}}{8}\\ = \frac{6}{5}.(\frac{{15}}{4} – \frac{{23}}{4}) + \frac{{16}}{7}.(\frac{{ – 85}}{8} + \frac{{71}}{8})\\ = \frac{6}{5}.\frac{{ – 8}}{4} + \frac{{16}}{7}.\frac{{ – 14}}{8}\\ = \frac{6}{5}.( – 2) + ( – 4)\\ = \frac{{ – 12}}{5} + \frac{{ – 20}}{5}\\ = \frac{{ – 32}}{5}$

Chú ý: Nếu phân số chưa tối giản, ta nên tối giản phân số trước để việc tính toán được thuận tiện hơn.

Bài trước:

👉 Giải bài 7 8 9 10 11 trang 13 sgk Toán 7 tập 1 Kết Nối Tri Thức

Bài tiếp theo:

👉 Giải bài 18 19 20 21 22 23 24 25 trang 18 19 sgk Toán 7 tập 1 Kết Nối Tri Thức

Trên đây là bài Hướng dẫn Giải bài 12 13 14 15 16 17 trang 14 15 sgk Toán 7 tập 1 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!

“Bài tập nào khó đã có giaibaisgk.com“