Nội Dung
Hướng dẫn giải Bài §12. Hình bình hành sgk Toán 8 tập 1 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 13 14 15 16 17 18 trang 61 sgk Toán 8 tập 1 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
Bài 12 HÌNH BÌNH HÀNH
Bài toán mở đầu trang 57 Toán 8 tập 1 KNTT
Hai con đường lớn $a$ và $b$ cắt nhau tạo thành một góc. Bên trong góc đó có một điểm dân cư $O$. Phải mở một con đường thẳng đi qua $O$ cắt $a$ tại $A$, cắt $b$ tại $B$ như thế nào để hai đoạn đường $OA$ và $OB$ bằng nhau (các con đường đều là đường thẳng) (H.3.27)?

Trả lời:
Gọi điểm giao nhau giữa hai đường thẳng $a$ và $b$ là điểm $C$.
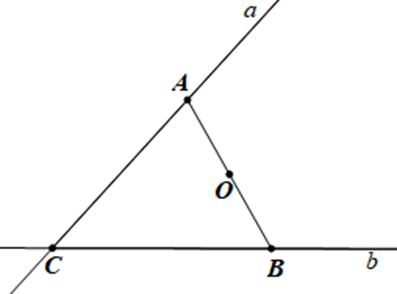
– Vẽ tia $Cx$ đi qua điểm $O$. Trên tia $Cx$ lấy điểm $D$ sao cho $OC = OD$ (hay $O$ là trung điểm của $CD$).
– Qua $D$ vẽ tia $Dy // a$ cắt tia $b$ tại $B$; vẽ $Dz // b$ cắt $a$ tại $A$.

Khi đó tứ giác $ACBD$ có $AC // BD; AD // BC$ nên là hình bình hành.
Suy ra hai đường chéo $AB, CD$ cắt nhau tại trung điểm của mỗi đường.
Mà $O$ là trung điểm $CD$ nên $O$ là trung điểm của $AB$, hay $OA = OB$.
Vậy con đường đi qua $O$ sao cho $OA = OB$ được mở như trên.
1. HÌNH BÌNH HÀNH VÀ TÍNH CHẤT
Hoạt động 1 trang 57 Toán 8 tập 1 KNTT
Trong Hình 3.28, có một hình bình hành. Đó là hình nào? Em có thể giải thích tại sao không?

Trả lời:
Tứ giác trong Hình 3.28c là hình bình hành vì:
Ta so sánh độ dài các cạnh đối trong tứ giác bằng cách đếm số ô vuông trong hình.
Ta thấy $AB = CD; AD = BC$.
Thực hành 1 trang 58 Toán 8 tập 1 KNTT
Vẽ hình bình hành, biết hai cạnh liên tiếp bằng $3 cm, 4 cm$ và góc xen giữa hai cạnh đó bằng $60^o$. Hãy mô tả cách vẽ và giải thích tại sao hình vẽ được là hình bình hành.
Trả lời:
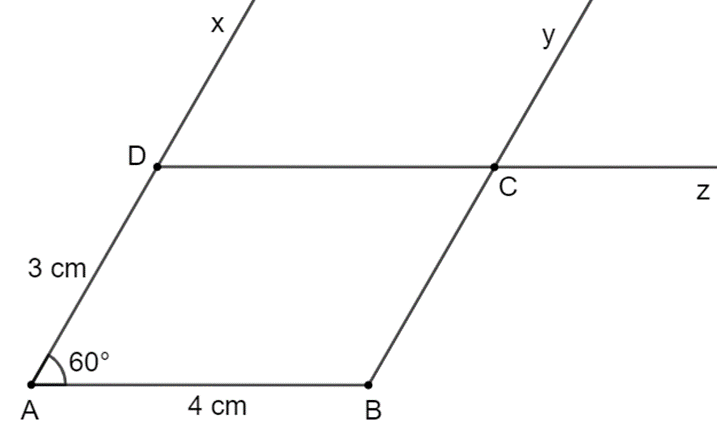
Giả sử hình bình hành $ABCD$ có $AD = 3cm, AB = 4 cm$ và \(\widehat {BA{\rm{D}}} = {60^o}\).
Cách vẽ:
– Vẽ cạnh $AB = 4 cm$.
– Vẽ \(\widehat {BAx} = {60^o}\). Trên tia $Ax$ lấy điểm $D$ sao cho $AD = 3cm$.
– Kẻ $By // AD, Dz // BC$. Hai tia $By$ và $Dz$ cắt nhau tại $C$, ta được hình bình hành $ABCD$.
Hình vẽ được là hình bình hành vì có hai cặp cạnh đối song song $(AB // CD, AD // BC)$.
Hoạt động 2 trang 58 Toán 8 tập 1 KNTT
Hãy nêu các tính chất của hình bình hành mà em đã biết.
Trả lời:
Các tính chất của hình bình hành mà em đã biết:
– Các cạnh đối song song;
– Các cạnh đối bằng nhau;
– Các góc đối bằng nhau;
– Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Hoạt động 3 trang 58 Toán 8 tập 1 KNTT
Cho hình bình hành $ABCD$ (H.3.30).
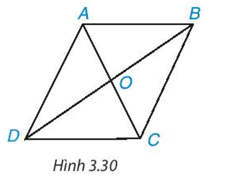
a) Chứng minh $∆ABC = ∆CDA$.
Từ đó suy ra $AB = CD, AD = BC$ và \(\widehat {ABC} = \widehat {CDA}\).
b) Chứng minh $∆ABD = ∆CDB$. Từ đó suy ra \(\widehat {DAB} = \widehat {BCD}\).
c) Gọi giao điểm của hai đường chéo $AC, BD$ là $O$. Chứng minh $∆AOB = ∆COD$. Từ đó suy ra $OA = OC, OB = OD$.
Trả lời:
a) Vì $ABCD$ là hình bình hành nên $AB // CD; AD // BC$.
Suy ra \(\widehat {BAC} = \widehat {ACD}; \,\widehat {BCA} = \widehat {DAC}\) (hai góc so le trong).
Xét $∆ABC$ và $∆CDA$ có:
\(\widehat {BAC} = \widehat {ACD}\) (chứng minh trên);
Cạnh $AC$ chung.
\(\widehat {BCA} = \widehat {DAC}\) (chứng minh trên);
Do đó $∆ABC = ∆CDA$ (g.c.g).
Suy ra $AB = CD, AD = BC$ (các cặp cạnh tương ứng); và \(\widehat {ABC} = \widehat {CDA}\) (hai góc tương ứng).
b) Xét $∆ABD$ và $∆CDB$ có:
$AB = CD$ (chứng minh trên);
$AD = BC$ (chứng minh trên);
Cạnh $BD$ chung.
Do đó $∆ABD = ∆CDB$ (c.c.c).
Suy ra \(\widehat {DAB} = \widehat {BCD}\) (hai góc tương ứng).
c) Xét $∆AOB$ và $∆COD$ có:
\(\widehat {BAC} = \widehat {ACD}\) (chứng minh trên);
$AB = CD$ (chứng minh trên);
\(\widehat {BCA} = \widehat {DAC}\) (chứng minh trên);
Do đó $∆AOB = ∆COD$ (g.c.g).
Suy ra $OA = OC, OB = OD$ (các cặp cạnh tương ứng).
Luyện tập 1 trang 58 Toán 8 tập 1 KNTT
Cho tam giác $ABC$. Từ một điểm $M$ tùy ý trên cạnh $BC$, kẻ đường thẳng song song với $AB$, cắt cạnh $AC$ tại $N$ và kẻ đường thẳng song song với $AC$, cắt $AB$ tại $P$. Gọi $I$ là trung điểm của đoạn $NP$. Chứng minh rằng $I$ cũng là trung điểm của đoạn thẳng $AM$.
Trả lời:
Ta có hình vẽ minh họa sau:
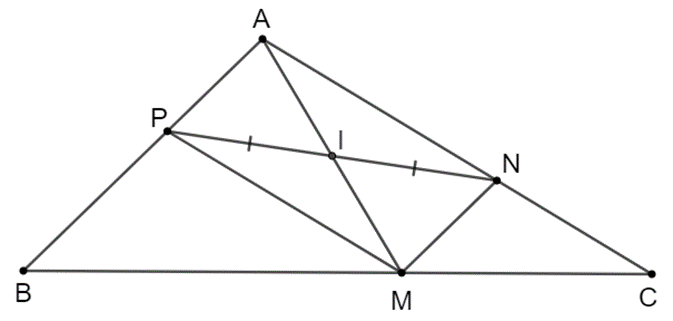
Xét tứ giác $APMN$ có:
• $MN // AP$ (vì $MN // AB$)
• $MP // AN$ (vì $MP // AC$)
Do đó tứ giác $APMN$ là hình bình hành.
Hình bình hành $APMN$ có $I$ là trung điểm của đoạn $AP$.
Do đó $I$ là trung điểm của đoạn thẳng $AM$ (đpcm).
Tranh luận trang 59 Toán 8 tập 1 KNTT

Theo em, bạn nào đúng? Vì sao?
Trả lời:
Khẳng định của bạn Vuông là đúng.
♦ Trường hợp 1: Hình thang có hai cạnh bên bằng nhau nhưng không song song với nhau thì hình thang đó là hình thang cân.
Hình minh họa:
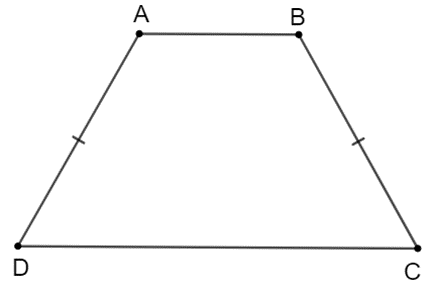
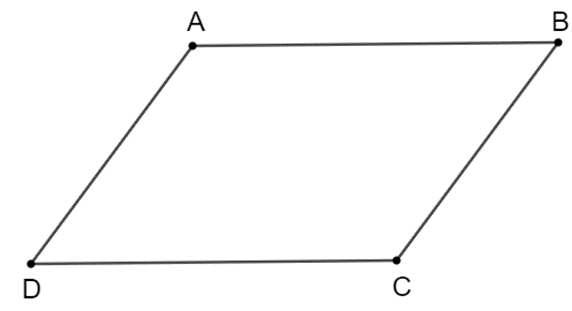
♦ Trường hợp 2: Hình thang có hai cạnh bên bằng nhau và song song với nhau thì hình thang đó là hình bình hành.
Hình minh họa:

2. DẤU HIỆU NHẬN BIẾT
Câu hỏi trang 59 Toán 8 tập 1 KNTT
Hãy viết giả thiết, kết luận của Định lí 2.
Trả lời:
Định lí 2:
a) Tứ giác có các cạnh đối bằng nhau là một hình bình hành.
b) Tứ giác có một cặp cạnh đối song song và bằng nhau là một hình bình hành.
Giả thiết, kết luận của Định lí 2:

Luyện tập 2 trang 60 Toán 8 tập 1 KNTT
Cho hình bình hành $ABCD (AB > BC)$. Tia phân giác của góc $D$ cắt $AB$ tại $E$ và tia phân giác của góc $B$ cắt $CD$ tại $F$ (H.3.32).
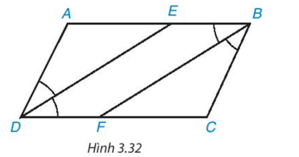
a) Chứng minh hai tam giác $ADE$ và $CBF$ là những tam giác cân, bằng nhau.
b) Tứ giác $DEBF$ là hình gì? Tại sao?
Trả lời:
Ta kí hiệu các góc như hình vẽ:

a) Vì $ABCD$ là hình bình hành nên $AB // CD$ hay $BE // DF$.
Vì $DE$ là tia phân giác của \(\widehat {ADC}\) nên \(\widehat {{D_1}} = \widehat {{D_2}}\)
Mà \(\widehat {{D_1}} = \widehat {{E_1}}\) ($BE // DF$, hai góc so le trong) nên \(\widehat {{D_2}} = \widehat {{E_1}}\)
Suy ra tam giác $ADE$ cân tại $A$.
Tương tự ta cũng chứng minh được: tam giác $BCF$ cân tại $C$.
Vì $ABCD$ là hình bình hành nên:
$AD = BC$; \(\widehat A = \widehat C; \,\widehat {ADC} = \widehat {ABC}\).
Vì $AE$ là tia phân giác \(\widehat {ADC}\); $BF$ là tia phân giác \(\widehat {ABC}\) nên
\(\widehat {{B_1}} = \widehat {{B_2}}; \,\widehat {{D_1}} = \widehat {{D_2}}\) mà \(\widehat {ADC} = \widehat {ABC}\)
Do đó \(\widehat {{B_1}} = \widehat {{B_2}} = \widehat {{D_1}} = \widehat {{D_2}}\)
Xét $∆ADE$ và $∆CBF$ có:
\(\widehat A = \widehat C\) (chứng minh trên);
$AD = BC$ (chứng minh trên);
\(\widehat {{B_2}} = \widehat {{D_2}}\) (chứng minh trên).
Do đó $∆ADE = ∆CBF$ (g.c.g).
b) Vì \(\widehat {{B_1}} = \widehat {{B_2}} = \widehat {{D_1}} = \widehat {{D_2}}\) mà \(\widehat {{B_2}} = \widehat {{F_1}}\) (vì tam giác $BCF$ cân tại $C$)
Suy ra \(\widehat {{D_1}} = \widehat {{F_1}}\) (hai góc đồng vị).
Do đó $DE // BF$
Tứ giác $BEDF$ có:
$BE // DF$ (chứng minh trên);
$DE // BF$ (chứng minh trên).
Do đó, tứ giác $BEDF$ là hình bình hành.
Thực hành 2 trang 60 Toán 8 tập 1 KNTT
Chia một sợi dây xích thành bốn đoạn: hai đoạn dài bằng nhau, hai đoạn ngắn bằng nhau và đoạn dài, đoạn ngắn xen kẽ nhau. Hỏi khi móc hai đầu mút của sợi dây xích đó lại để được một tứ giác $ABCD$ (có các đỉnh tại các điểm chia) như Hình 3.33 thì tứ giác $ABCD$ là hình gì? Tại sao?

Trả lời:
Đoạn dây xích được chia thành:
• Hai đoạn dài có độ dài bằng nhau, tức là $AB = CD$;
• Hai đoạn ngắn có độ dài bằng nhau, tức là $AD = BC$.
Tứ giác $ABCD$ có $AB = CD; \,AD = BC$ nên tứ giác $ABCD$ là hình bình hành.
Câu hỏi trang 60 Toán 8 tập 1 KNTT
Hãy biết giả thiết, kết luận của Định lí 3.
Trả lời:

Định lí 3:
a) Tứ giác có các góc đối bằng nhau là một hình bình hành.
b) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là một hình bình hành.
Giả thiết, kết luận của Định lí 3:

Luyện tập 3 trang 61 Toán 8 tập 1 KNTT
Cho hai điểm $A, B$ phân biệt và điểm $O$ không nằm trên đường thẳng $AB$. Gọi $A’, B’$ là các điểm sao cho $O$ là trung điểm của $AA’, BB’$. Chứng minh rằng $A’B’ = AB$ và đường thẳng $A’B’$ song song với đường thẳng $AB$.
Trả lời:
Ta có hình vẽ minh họa sau:
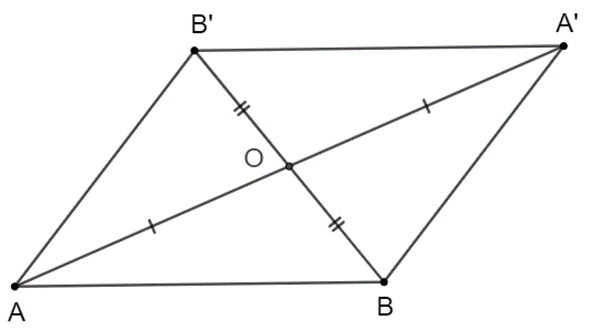
Ta có hai điểm $A, B$ phân biệt và điểm $O$ không nằm trên đường thẳng $AB$.
Mà $O$ là trung điểm của $AA’, BB’$ nên $O$ là trung điểm của hai đường chéo của tứ giác $ABA’B’$.
Do đó tứ giác $ABA’B’$ là hình bình hành.
Suy ra $A’B’ = AB$ và $A’B’ // AB$.
Vận dụng trang 61 Toán 8 tập 1 KNTT
Trở lại bài toán mở đầu. Em hãy vẽ hình và nêu cách vẽ con đường cần mở đi qua $O$ sao cho theo con đường đó, hai đoạn đường từ $O$ tới $a$ và tới $b$ bằng nhau.
Trả lời:
Gọi điểm giao nhau giữa hai đường thẳng $a$ và $b$ là điểm $C$.

– Vẽ tia $Cx$ đi qua điểm $O$. Trên tia $Cx$ lấy điểm $D$ sao cho $OC = OD$ (hay $O$ là trung điểm của $CD$).
– Qua $D$ vẽ tia $Dy // a$ cắt tia $b$ tại $B$; vẽ $Dz // b$ cắt $a$ tại $A$.

Khi đó tứ giác $ACBD$ có $AC // BD; AD // BC$ nên là hình bình hành.
Suy ra hai đường chéo $AB, CD$ cắt nhau tại trung điểm của mỗi đường.
Mà $O$ là trung điểm $CD$ nên $O$ là trung điểm của $AB$, hay $OA = OB$.
Vậy con đường đi qua $O$ sao cho $OA = OB$ được mở như trên.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 13 14 15 16 17 18 trang 61 sgk Toán 8 tập 1 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 3.13 trang 61 Toán 8 tập 1 KNTT
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Vì sao?
a) Hình thang có hai cạnh bên song song là hình bình hành.
b) Hình thang có hai cạnh bên bằng nhau là hình bình hành.
c) Tứ giác có hai cạnh đối nào cũng song song là hình bình hành.
Bài giải:
a) Hình thang là tứ giác có một cặp cạnh song song.
Suy ra hình thang có hai cạnh bên song song thì hình này có hai cặp cạnh đối song song.
Do đó hình thang có hai cạnh bên song song là hình bình hành.
Vậy khẳng định a) đúng.
b) Hình thang có hai cạnh bên bằng nhau nhưng không song song nên không phải là hình bình hành.
Vậy khẳng định b) sai.
c) Tứ giác có hai cạnh đối nào cũng song song hay có hai cặp cạnh đối song song nên tứ giác đó là hình bình hành.
Vậy khẳng định c) đúng.
Giải bài 3.14 trang 61 Toán 8 tập 1 KNTT
Tính các góc còn lại của hình bình hành ABCD trong Hình 3.35.
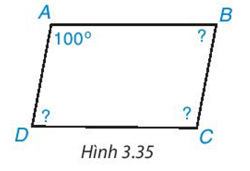
Bài giải:
Vì $ABCD$ là hình bình hành nên:
\(\widehat A = \widehat C = 100^o; \,\widehat B = \widehat D\)
Ta có:
$\widehat A + \widehat B + \widehat C + \widehat D = {360^o}$
$⇔ {100^o} + \widehat B + {100^o} + \widehat B = {360^o}$
$⇒ 2\widehat B + {200^o} = {360^o}$
\(⇒ 2\widehat B = {360^o} – {200^o} = {160^o}\)
Do đó: \(\widehat B = {80^o}\) suy ra: \(\widehat B = \widehat D = {80^o}\)
Vậy các góc của hình bình hành $ABCD$ là: \(\widehat A = {100^o}; \,\widehat C = {100^o}; \,\widehat B = {80^o}; \,\widehat D = {80^o}\).
Giải bài 3.15 trang 61 Toán 8 tập 1 KNTT
Cho hình bình hành $ABCD$. Gọi $E, F$ lần lượt là trung điểm của $AB, CD$. Chứng minh $BF = DE$.
Bài giải:
Ta có hình vẽ minh họa sau:
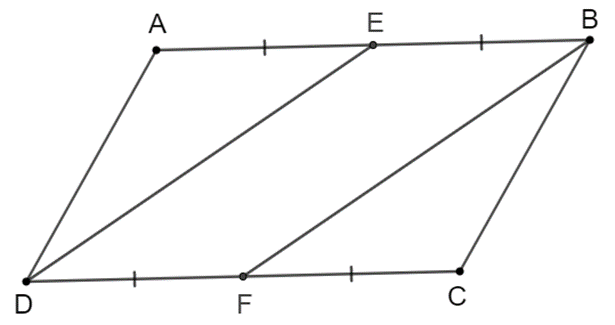
Vì $ABCD$ là hình bình hành nên $AB = CD, \,AB // CD$.
Mà $E, F$ lần lượt là trung điểm của $AB, CD$ nên $AE = BE, \,CF = DF$.
Do đó $AE = BE = CF = DF$.
Xét tứ giác $BEDF$ có:
$BE = DF$ (chứng minh trên);
$BE // DF$ (vì $AB // CD$)
Do đó tứ giác $BEDF$ là hình bình hành.
Suy ra $BF = DE$ (đpcm).
Giải bài 3.16 trang 61 Toán 8 tập 1 KNTT
Trong mỗi trường hợp sau đây, tứ giác nào là hình bình hành, tứ giác nào không là hình bình hành? Vì sao?

Bài giải:
♦ Hình 3.36a):
Xét tứ giác $ABCD$ có:
\(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
$⇔ 100^o+80^o+100^o+\widehat D = {360^o}$
$⇔ 280^o+\widehat D=360^o$
Suy ra \(\widehat D=360^o−280^o=80^o\)
Tứ giác $ABCD$ có: \(\widehat A = \widehat C=100^o\); \(\widehat B = \widehat D=80^o\)
Do đó, tứ giác $ABCD$ là hình bình hành.
♦ Hình 3.36b):
Xét tứ giác $ABCD$ có:
\(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
$⇔ 75^o+ \widehat B +75^o+90^o=360^o$
$⇔ 240^o+ \widehat B =360^o$
Suy ra \(\widehat B=360^o−240^o=120^o\)
Tứ giác $ABCD$ có: \(\widehat A = \widehat C=100^o\) nhưng \(\widehat B \ne \widehat D\) ($120^o≠90^o$)
Do đó, tứ giác $ABCD$ không là hình bình hành.
♦ Hình 3.36c):
Xét tứ giác $ABCD$ có:
\(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
$⇔ 70^o+110^o+ \widehat C +110^o=360^o$
$⇔ \widehat C +290^o=360^o$
Suy ra \(\widehat C=360^o−290^o=70^o\)
Tứ giác $ABCD$ có: \(\widehat A = \widehat C=70^o\); \(\widehat B = \widehat D=110^o\)
Do đó, tứ giác $ABCD$ là hình bình hành.
Vậy tứ giác $ABCD$ trong Hình 3.36a) và 3.36c) là hình bình hành; tứ giác $ABCD$ trong Hình 3.36b) không là hình bình hành.
Giải bài 3.17 trang 61 Toán 8 tập 1 KNTT
Cho hình bình hành $ABCD$. Gọi $E, F$ lần lượt là trung điểm của các cạnh $AB, CD$. Chứng minh rằng:
a) Hai tứ giác $AEFD, \,AECF$ là những hình bình hành;
b) $EF = AD, \,AF = EC$.
Bài giải:
Ta có hình vẽ minh họa sau:
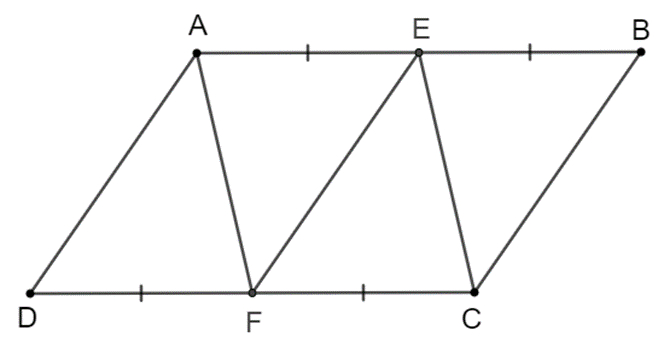
a) Vì $ABCD$ là hình bình hành nên $AB = CD, \,AB // CD$.
Mà $E, F$ lần lượt là trung điểm của $AB, CD$ nên $AE = BE, \,CF = DF$.
Do đó $AE = BE = CF = DF$.
♦ Xét tứ giác $AEFD$ có:
$AE // DF$ (vì $AB // CD$);
$AE = DF$ (chứng minh trên)
Do đó tứ giác $AEFD$ là hình bình hành.
♦ Xét tứ giác $AECF$ có:
$AE // CF$ (vì $AB // CD$);
$AE = CF$ (chứng minh trên)
Do đó tứ giác $AECF$ là hình bình hành.
Vậy hai tứ giác $AEFD, AECF$ là những hình bình hành.
b) Vì tứ giác $AEFD$ là hình bình hành nên $EF = AD$.
Vì tứ giác $AECF$ là hình bình hành nên $AF = EC$.
Vậy $EF = AD, \,AF = EC$.
Giải bài 3.18 trang 61 Toán 8 tập 1 KNTT
Gọi $O$ là giao điểm của hai đường chéo của hình bình hành $ABCD$. Một đường thẳng đi qua $O$ lần lượt cắt các cạnh $AB, CD$ của hình bình hành tại hai điểm $M, N$. Chứng minh $∆OAM = ∆OCN$. Từ đó suy ra tứ giác $MBND$ là hình bình hành.
Bài giải:
Ta có hình vẽ minh họa sau:
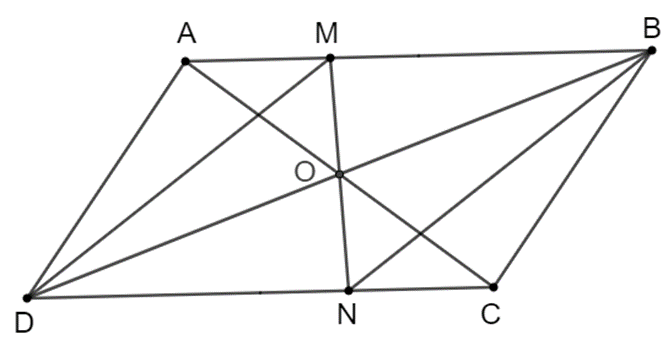
Vì $ABCD$ là hình bình hành nên ta có:
• Hai đường chéo $AC$ và $BD$ cắt nhau tại $O$ nên $OA = OC, \,OB = OD$.
• $AB // CD$ nên $AM // CN$
Suy ra \(\widehat {OAM} = \widehat {OCN}\) (hai góc so le trong).
Xét $∆OAM$ và $∆OCN$ có:
\(\widehat {OAM} = \widehat {OCN}\) (chứng minh trên)
$OA = OC$ (chứng minh trên)
\(\widehat {AOM} = \widehat {CON}\) (hai góc đối đỉnh)
Do đó $∆OAM = ∆OCN$ (g.c.g).
Suy ra $AM = CN$ (hai cạnh tương ứng)
Mặt khác, $AB = CD$ (chứng minh trên);
$AB = AM + BM$;
$CD = CN + DN$
Suy ra $BM = DN$.
Xét tứ giác $MBND$ có:
• $BM // DN$ (vì $AB // CD$)
• $BM = DN$ (chứng minh trên)
Do đó, tứ giác $MBND$ là hình bình hành.
Bài trước:
👉 Giải bài 9 10 11 12 trang 56 sgk Toán 8 tập 1 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải bài 19 20 21 22 23 24 trang 63 sgk Toán 8 tập 1 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải bài 13 14 15 16 17 18 trang 61 sgk Toán 8 tập 1 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
