Giải bài 27 28 29 30 31 32 33 trang 21 sgk Toán 6 tập 2 Kết Nối Tri Thức

Nội Dung

Hướng dẫn giải Bài 26. Phép nhân và phép chia phân số sgk Toán 6 tập 2 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 27 28 29 30 31 32 33 trang 21 sgk Toán 6 tập 2 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 6.

BÀI 26. PHÉP NHÂN VÀ PHÉP CHIA PHÂN SỐ

Bài toán mở đầu trang 19 Toán 6 tập 2 KNTT

Mẹ Minh dành $\dfrac{2}{3}$ tiền lương hàng tháng để chi tiêu trong gia đình. $\dfrac{1}{5}$ số tiền chi tiêu đó là tiền bán trú cho Minh. Hỏi tiền bán trú cho Minh bằng bao nhiêu phần tiền lương hàng tháng của mẹ?

Trả lời:

Sau khi học xong bài học này, ta sẽ biết được số tiền bán trú của mình bằng:

$\dfrac{1}{5}:\dfrac{2}{3}=\dfrac{1}{5}.\dfrac{3}{2}=\dfrac{3}{10}$ (phần tiền lương tháng của mẹ).

1. PHÉP NHÂN HAI PHÂN SỐ

Hoạt động 1 trang 19 Toán 6 tập 2 KNTT

Em hãy nhớ lại quy tắc nhân hai phân số (có tử và mẫu đều dương), rồi tính $\dfrac{8}{3}.\dfrac{3}{7}$ và $\dfrac{4}{6}.\dfrac{5}{8}$.

Trả lời:

– Quy tắc nhân 2 phân số: Nhân tử với tử, mẫu với mẫu.

– Áp dụng:

$\dfrac{8}{3}.\dfrac{3}{7} = \dfrac{{8.3}}{{3.7}} = \dfrac{{24}}{{21}} = \dfrac{{24:3}}{{21:3}} = \dfrac{8}{7}$

$\dfrac{4}{6}.\dfrac{5}{8} = \dfrac{{4.5}}{{6.8}} = \dfrac{{20}}{{48}} = \dfrac{{20:4}}{{48:4}} = \dfrac{5}{{12}}$

Luyện tập 1 trang 19 Toán 6 tập 2 KNTT

Tính:

a) $\dfrac{{ – 2}}{5}.\dfrac{5}{4}$;

b) $\dfrac{{ – 7}}{{10}}.\dfrac{{ – 9}}{{11}}$.

Trả lời:

a) Ta có:

$\dfrac{{ – 2}}{5}.\dfrac{5}{4}$$ = \dfrac{{ – 2.5}}{{5.4}} = \dfrac{{ – 10}}{{20}} = \dfrac{{ – 10:10}}{{20:10}} = \dfrac{{ – 1}}{2}$

b) Ta có:

$\dfrac{{ – 7}}{{10}}.\dfrac{{ – 9}}{{11}}$$ = \dfrac{{ – 7.\left( { – 9} \right)}}{{10.11}} = \dfrac{{63}}{{110}}$

Vận dụng 1 trang 20 Toán 6 tập 2 KNTT

Tính diện tích hình tam giác biết một cạnh dài $\dfrac{9}{5}cm$, chiều cao ứng với cạnh đó bằng $\dfrac{7}{3}cm$.

Trả lời:

Diện tích hình tam giác là:

$\dfrac{1}{2}. \dfrac{9}{5}.\dfrac{7}{3}= \dfrac{{1.9.7}}{{2.5.3}} = \dfrac{{21}}{10}\left( {c{m^2}} \right)$

2. TÍNH CHẤT CỦA PHÉP NHÂN

Luyện tập 2 trang 20 Toán 6 tập 2 KNTT

Tính:

a) $\dfrac{6}{{13}}.\dfrac{8}{7}.\dfrac{{ – 26}}{3}.\dfrac{{ – 7}}{8}$;

b) $\dfrac{6}{5}.\dfrac{3}{{13}} – \dfrac{6}{5}.\dfrac{{16}}{{13}}$.

Trả lời:

a) Ta có:

$\dfrac{6}{{13}}.\dfrac{8}{{7}}.\dfrac{{ – 26}}{3}.\dfrac{{ – 7}}{8}$

$= \left( {\dfrac{6}{{13}}.\dfrac{{ – 26}}{3}} \right).\left( {\dfrac{8}{7}.\dfrac{{ – 7}}{8}} \right)\\ = \dfrac{{6.\left( { – 26} \right)}}{{13.3}}.\dfrac{{8.\left( { – 7} \right)}}{{7.8}}\\= (- 4).\left( { – 1} \right) = 4$

b) Ta có:

$\dfrac{6}{5}.\dfrac{3}{{13}} – \dfrac{6}{5}.\dfrac{{16}}{{13}}$

$= \dfrac{6}{5}.\left( {\dfrac{3}{{13}} – \dfrac{{16}}{{13}}} \right)\\ = \dfrac{6}{5}.\dfrac{{3 – 16}}{{13}}\\ = \dfrac{6}{5}.\dfrac{{-13}}{{13}}\\= \dfrac{6}{5}.\left( { – 1} \right)\\ = \dfrac{{ – 6}}{5}$.

3. PHÉP CHIA PHÂN SỐ

Hoạt động 2 trang 20 Toán 6 tập 2 KNTT

Tính các tích sau: $\dfrac{5}{4}.\dfrac{4}{5}$; $\dfrac{{ – 5}}{7}.\dfrac{7}{{ – 5}}$.

Trả lời:

Ta có:

$\dfrac{5}{4}.\dfrac{4}{5} = \dfrac{{5.4}}{{4.5}} = \dfrac{{20}}{{20}} = 1$;

$\dfrac{{ – 5}}{7}.\dfrac{7}{{ – 5}} = \dfrac{{ – 5.7}}{{7.\left( { – 5} \right)}} = \dfrac{{ – 35}}{{ – 35}} = 1$.

Câu hỏi trang 20 Toán 6 tập 2 KNTT

Em hãy tìm phân số nghịch đảo của 11 và $\dfrac{7}{{ – 5}}$.

Trả lời:

Ta có:

Phân số nghịch đảo của 11 là $\dfrac{1}{{11}}$.

Phân số nghịch đảo của $\dfrac{7}{{ – 5}}$ là $\dfrac{{ – 5}}{7}$.

Hoạt động 3 trang 21 Toán 6 tập 2 KNTT

Em hãy nhắc lại quy tắc chia hai phân số có tử và mẫu đều dương, rồi tính $\dfrac{3}{4}:\dfrac{2}{5}$.

Trả lời:

– Quy tắc chia hai phân số có tử mẫu đều dương: Lấy số bị chia nhân với phân số nghịch đảo của số chia.

– Áp dụng:

$\dfrac{3}{4}:\dfrac{2}{5} = \dfrac{3}{4}.\dfrac{5}{2} = \dfrac{{3.5}}{{4.2}} = \dfrac{{15}}{8}$

Luyện tập 3 trang 21 Toán 6 tập 2 KNTT

Tính:

a) $\dfrac{{ – 8}}{9}:\dfrac{4}{3}$;

b) $\left( { – 2} \right):\dfrac{2}{5}$.

Trả lời:

a) Ta có:

$\dfrac{{ – 8}}{9}:\dfrac{4}{3}$

$ = \dfrac{{ – 8}}{9}.\dfrac{3}{4} = \dfrac{{ – 8.3}}{{9.4}} = \dfrac{{ – 2}}{3}$

b) Ta có:

$\left( { – 2} \right):\dfrac{2}{5}$$ = \left( { – 2} \right).\dfrac{5}{2} = \dfrac{{ – 2.5}}{2} = – 5$

Vận dụng 2 trang 21 Toán 6 tập 2 KNTT

Trong một công thức làm bánh, An cần $\dfrac{3}{4}$ cốc đường để làm 9 cái bánh. Nếu An chỉ muốn làm 6 cái bánh thì cần bao nhiêu cốc đường?

Trả lời:

Để làm 1 cái bánh thì cần:

$\dfrac{3}{4}:9 = \dfrac{3}{4}.\dfrac{1}{9} = \dfrac{1}{{12}}$ (cốc đường)

Để làm 6 cái bánh thì cần:

$\dfrac{1}{{12}}.6 = \dfrac{1}{2}$ (cốc đường)

Vậy để làm 6 cái bánh thì cần $\dfrac{1}{2}$ cốc đường.

GIẢI BÀI TẬP

Sau đây là phần Giải bài 27 28 29 30 31 32 33 trang 21 sgk Toán 6 tập 2 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 6.27 trang 21 Toán 6 tập 2 KNTT

Thay dấu “?” bằng số thích hợp trong bảng sau:

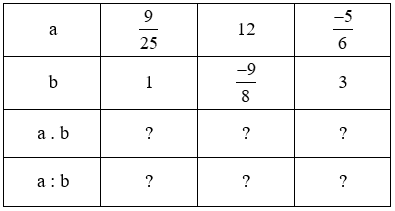
Bài giải:

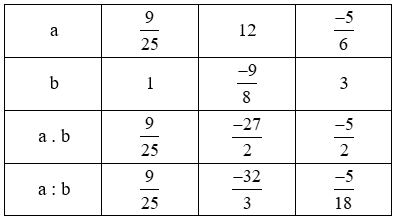
– Ở cột thứ hai: với $a = \dfrac{9}{{25}}, b = 1$ nên:

Dấu “?” đầu tiên là $? = a.b = \dfrac{9}{{25}}.1 = \dfrac{9}{{25}}$

Dấu “?” thứ hai là $? = a:b = \dfrac{9}{{25}}:1 = \dfrac{9}{{25}}$

– Ở cột thứ ba: với $a = 12,b = \dfrac{{ – 9}}{8}$ nên:

Dấu “?” đầu tiên là $? = a.b 12.\dfrac{{ – 9}}{8} = \dfrac{{12.\left( { – 9} \right)}}{{.8}} = \dfrac{{ – 27}}{2}$

Dấu “?” thứ hai là $? = a:b = 12:\dfrac{{ – 9}}{8} = 12.\dfrac{8}{{ – 9}} = \dfrac{{12.8}}{{ – 9}} = \dfrac{{ – 32}}{3}$

– Ở cột thứ tư: với $a = \dfrac{{ – 5}}{6}, b = 3$ nên

Dấu “?” đầu tiên là $? = a.b = \dfrac{{ – 5}}{6}.3 = \dfrac{{ – 5}}{2}$

Dấu “?” thứ hai là $? = a:b = \dfrac{{ – 5}}{6}:3 = \dfrac{{ – 5}}{6}.\dfrac{1}{3} = \dfrac{{ – 5}}{{18}}$

Vậy ta có bảng sau:

Giải bài 6.28 trang 21 Toán 6 tập 2 KNTT

Tính:

a) $\dfrac{7}{8} + \dfrac{7}{8}:\dfrac{1}{8} – \dfrac{1}{2}$;

b) $\dfrac{6}{{11}} + \dfrac{{11}}{3}.\dfrac{3}{{22}}$.

Bài giải:

a) Ta có:

$\dfrac{7}{8} + \dfrac{7}{8}:\dfrac{1}{8} – \dfrac{1}{2}$

$= \dfrac{7}{8} + \dfrac{7}{8}.8 – \dfrac{1}{2}\\ = \dfrac{7}{8}.1 + \dfrac{7}{8}.8 – \dfrac{1}{2}\\ = \left( {\dfrac{7}{8}.1 + \dfrac{7}{8}.8} \right) – \dfrac{1}{2}\\ = \dfrac{7}{8}.\left( {1 + 8} \right) – \dfrac{1}{2} = \dfrac{7}{8}.9 – \dfrac{1}{2}\\ = \dfrac{{63}}{8} – \dfrac{1}{2} = \dfrac{{63}}{8} – \dfrac{4}{8} = \dfrac{{63 – 4}}{8} = \dfrac{{59}}{8}$

b) Ta có:

$\dfrac{6}{{11}} + \dfrac{{11}}{3}.\dfrac{3}{{22}}$

$= \dfrac{6}{{11}} + \dfrac{{11.3}}{{3.22}} = \dfrac{6}{{11}} + \dfrac{1}{2}\\ = \dfrac{{12}}{{22}} + \dfrac{{11}}{{22}} = \dfrac{{12 + 11}}{{22}} = \dfrac{{23}}{{22}}$

Giải bài 6.29 trang 21 Toán 6 tập 2 KNTT

Tính một cách hợp lí:

a) $\dfrac{3}{4}.\dfrac{1}{{13}} – \dfrac{3}{4}.\dfrac{{14}}{{13}}$;

b) $\dfrac{5}{{13}}.\dfrac{{ – 3}}{{10}}.\dfrac{{ – 13}}{5}$.

Bài giải:

Ta có thể tính như sau

a) Ta có:

$\dfrac{3}{4}.\dfrac{1}{{13}} – \dfrac{3}{4}.\dfrac{{14}}{{13}}$

$= \dfrac{3}{4}.\left( {\dfrac{1}{{13}} – \dfrac{{14}}{{13}}} \right) = \dfrac{3}{4}.\left( {\dfrac{{1 – 14}}{{13}}} \right)\\ = \dfrac{3}{4}.\dfrac{{-13}}{{13}} = \dfrac{3}{4}.(-1 )= \dfrac{-3}{4}$

b) Ta có:

$\dfrac{5}{{13}}.\dfrac{{ – 3}}{{10}}.\dfrac{{ – 13}}{5}$

$= \dfrac{5}{{13}}.\dfrac{{ – 13}}{5}.\dfrac{{ – 3}}{{10}} = \left( {\dfrac{5}{{13}}.\dfrac{{ – 13}}{5}} \right).\dfrac{{ – 3}}{{10}}\\ = \dfrac{{5.\left( { – 13} \right)}}{{13.5}}.\dfrac{{ – 3}}{{10}} = \left( { – 1} \right).\dfrac{{ – 3}}{{10}} = \dfrac{3}{{10}}$

Giải bài 6.30 trang 21 Toán 6 tập 2 KNTT

Mỗi buổi sáng, Nam thường đi xe đạp từ nhà đến trường với vận tốc 15 km/h và hết 20 phút. Hỏi quãng đường từ nhà Nam đến trường dài bao nhiêu ki lô mét?

Bài giải:

Đổi $20$ phút = $\dfrac{{20}}{{60}}$ giờ = $\dfrac{1}{3}$ giờ.

Quãng đường từ nhà Nam đến trường là:

$15.\dfrac{1}{3} = \dfrac{{15}}{3} = 5km$

Vậy quãng đường từ nhà Nam đến trường dài $5$ km.

Giải bài 6.31 trang 21 Toán 6 tập 2 KNTT

Một hình chữ nhật có chiều dài là $\dfrac{7}{2}$ cm, diện tích là $\dfrac{{21}}{{10}}c{m^2}$. Tìm chiều rộng của hình chữ nhật

Bài giải:

Chiều rộng hình chữ nhật là:

$\dfrac{{21}}{{10}}:\dfrac{7}{2} = \dfrac{{21}}{{10}}.\dfrac{2}{7} = \dfrac{3}{5} \,cm$

Vậy chiều rộng của hình chữ nhật dài $\dfrac{3}{5}$ cm.

Giải bài 6.32 trang 21 Toán 6 tập 2 KNTT

Tìm $x$, biết:

a) $x.\dfrac{7}{2} = \dfrac{7}{9}$;

b) $x:\dfrac{8}{5} = \dfrac{5}{2}$.

Bài giải:

a) Ta có:

$x.\dfrac{7}{2} = \dfrac{7}{9}$

$⇔ x = \dfrac{7}{9}:\dfrac{7}{2}\\⇔ x = \dfrac{7}{9}.\dfrac{2}{7}\\⇔ x =\dfrac{2}{9}$

Vậy $x =\dfrac{2}{9}$.

b) Ta có:

$x:\dfrac{8}{5} = \dfrac{5}{2}\\⇔ x = \dfrac{5}{2}.\dfrac{8}{5}\\⇔ x = 4$

Vậy $x =4$.

Giải bài 6.33 trang 21 Toán 6 tập 2 KNTT

Lớp 6A có $\dfrac{1}{3}$ số học sinh thích môn Toán. Trong số các học sinh thích môn Toán, có $\dfrac{1}{2}$ số học sinh thích môn Ngữ văn. Hỏi có bao nhiêu phần số học sinh lớp 6A thích cả môn Toán và Ngữ văn?

Bài giải:

Số phần học sinh thích cả môn Toán và môn Ngữ văn trong lớp 6A là:

$\dfrac{1}{2}.\dfrac{1}{3} = \dfrac{{1.1}}{{2.3}} = \dfrac{1}{6}$ (học sinh lớp 6A)

Vậy lớp 6A có $\dfrac{1}{6}$ số học sinh thích cả môn Toán và Ngữ Văn.

Bài trước:

👉 Giải bài 21 22 23 24 25 26 trang 18 sgk Toán 6 tập 2 Kết Nối Tri Thức

Bài tiếp theo:

👉 Giải bài 34 35 36 37 trang 24 sgk Toán 6 tập 2 Kết Nối Tri Thức

Trên đây là bài Hướng dẫn Giải bài 27 28 29 30 31 32 33 trang 21 sgk Toán 6 tập 2 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 6 tốt nhất!

“Bài tập nào khó đã có giaibaisgk.com“