Nội Dung
Hướng dẫn giải Bài §16. Đường trung bình của tam giác sgk Toán 8 tập 1 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài Giải bài 6 7 8 9 trang 83 sgk Toán 8 tập 1 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
Bài 16 ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC
Bài toán mở đầu trang 81 Toán 8 tập 1 KNTT
Cho $B$ và $C$ là hai điểm cách nhau bởi một hồ nước như Hình 4.12 với $D, E$ lần lượt là trung điểm của $AB$ và $AC$. Biết $DE = 500 m$, liệu không cần đo trực tiếp, ta có thể tính được khoảng cách giữa hai điểm $B$ và $C$ không?

Trả lời:
Trong tam giác $ABC$ có $D, E$ lần lượt là trung điểm của $AB$ và $AC$ nên:
$D ∈ AB; \,E ∈ AC$ và $AD = BD; \,AE = EC$
Suy ra $DE$ là đường trung bình của tam giác $ABC$.
Do đó \(DE = \frac{1}{2}BC\) suy ra $BC = 2DE = 2 . 500 = 1 000 (m)$
Vậy khoảng cách giữa hai điểm $B$ và $C$ bằng $1 000 m$.
1. ĐỊNH NGHĨA ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC
Câu hỏi trang 81 Toán 8 tập 1 KNTT
Em hãy chỉ ra các đường trung bình của $∆DEF$ và $∆IHK$ trong Hình 4.14.

Trả lời:
Quan sát Hình 4.14, ta thấy:
♦ Xét $∆DEF$ có $M$ là trung điểm của cạnh $DE; N$ là trung điểm của cạnh $DF$ nên $MN$ là đường trung bình của $∆DEF$.
♦ Xét ∆IHK có:
• $B$ là trung điểm của cạnh $IH; C$ là trung điểm của cạnh $IK$ nên $BC$ là đường trung bình của $∆DEF$.
• $B$ là trung điểm của cạnh $IH; A$ là trung điểm của cạnh $HK$ nên $AB$ là đường trung bình của $∆DEF$.
• $A$ là trung điểm của cạnh $HK; C$ là trung điểm của cạnh $IK$ nên $AC$ là đường trung bình của $∆DEF$.
Vậy đường trung bình của $∆DEF$ là $MN$; các đường trung bình của $∆IHK$ là $AB, \,BC, \,AC$.
2. TÍNH CHẤT ĐƯỜNG TRUNG BÌNH CỦA TAM GIÁC
Hoạt động 1 trang 82 Toán 8 tập 1 KNTT
Cho DE là đường trung bình của tam giác $ABC$ (H.4.15)

Sử dụng định lí Thalès đảo, chứng minh rằng $DE // BC$.
Trả lời:
Ta có $AD = BD$ và $D ∈ AB$ nên $D$ là trung điểm của $AB$;
$AE = EC$ và $E ∈ AC$ nên $E$ là trung điểm của $AC$.
Xét tam giác $ABC$ có $D, \,E$ lần lượt là trung điểm của $AB$ và $AC$, theo định lí Thalès đảo, ta suy ra $DE // BC$ (đpcm).
Hoạt động 2 trang 82 Toán 8 tập 1 KNTT
Gọi $F$ là trung điểm của $BC$. Chứng minh tứ giác $DEFB$ là hình bình hành. Từ đó suy ra \(DE = \frac{1}{2}BC\).
Trả lời:
Chứng minh tương tự HĐ1, ta có $EF // AB$.
Xét tam giác $DEFB$ có $DE // BF, \,EF // BD$
⇒ $DEFB$ là hình bình hành.
Suy ra $DE = BF$ (hai cạnh tương ứng)
Mà $F$ là trung điểm của $BC$ Suy ra $BF = \frac{1}{2}BC$
Suy ra $DE = \frac{1}{2}BC$.
Luyện tập trang 83 Toán 8 tập 1 KNTT
Cho tam giác $ABC$ cân tại $A, D$ và $E$ lần lượt là trung điểm của $AB, AC$. Tứ giác $DECB$ là hình gì? Tại sao?
Trả lời:
Ta có hình vẽ minh họa sau:
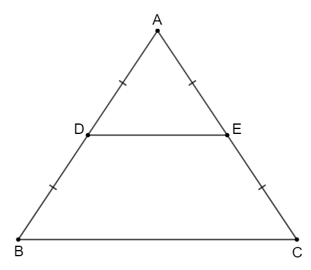
Tam giác $ABC$ cân tại $A$ nên \(\widehat B = \widehat C\)
Vì $D$ và $E$ lần lượt là trung điểm của $AB, AC$ nên $DE$ là đường trung bình của tam giác $ABC$.
Suy ra $DE // BC$ nên tứ giác $DECB$ là hình thang.
Hình thang $DECB$ có \(\widehat B = \widehat C\) nên tứ giác $DECB$ là hình thang cân.
Vận dụng trang 83 Toán 8 tập 1 KNTT
Em hãy trả lời câu hỏi trong tình huống mở đầu.
Trả lời:
Trong tam giác $ABC$ có $D, E$ lần lượt là trung điểm của $AB$ và $AC$ nên:
$D ∈ AB; \,E ∈ AC$ và $AD = BD; \,AE = EC$
Suy ra $DE$ là đường trung bình của tam giác $ABC$.
Do đó \(DE = \frac{1}{2}BC\) suy ra $BC = 2DE = 2 . 500 = 1 000 (m)$
Vậy khoảng cách giữa hai điểm $B$ và $C$ bằng $1 000 m$.
GIẢI BÀI TẬP
Sau đây là phần Giải bài 6 7 8 9 trang 83 sgk Toán 8 tập 1 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 4.6 trang 83 Toán 8 tập 1 KNTT
Tính các độ dài $x, \,y$ trong Hình 4.18.

Bài giải:
♦ Hình 4.18a):
Ta có:
$DH = HF, \,H ∈ DF$ nên $H$ là trung điểm của $DF$
$EK = KF, \,K ∈ EF$ nên $K$ là trung điểm của $EF$
Xét tam giác $DEF$ có $H, K$ lần lượt là trung điểm của $DF, EF$ nên $HK$ là đường trung bình của tam giác $DEF$
Suy ra \(HK = \frac{1}{2}DE = \frac{1}{2}x\)
Do đó $x = 2HK = 2 . 3 = 6$.
♦ Hình 4.18b):
Vì $MN ⊥ AB, \,AC ⊥ AB$ nên $MN // AC$.
Mà $M$ là trung điểm của $BC$ (vì $AM = BM = 3$)
Suy ra $MN$ là đường trung bình của tam giác $ABC$.
Do đó $y = NC = BN = 5$.
Vậy $x = 6; \,y = 5$.
Giải bài 4.7 trang 83 Toán 8 tập 1 KNTT
Cho tam giác $ABC$. Gọi $M, N, P$ lần lượt là trung điểm của các cạnh $AB, AC, BC$.
a) Chứng minh tứ giác $BMNC$ là hình thang.
b) Tứ giác $MNPB$ là hình gì? Tại sao?
Bài giải:
Ta có hình vẽ minh họa sau:

a) Vì $M, N$ lần lượt là trung điểm của các cạnh $AB, AC$ nên $MN$ là đường trung bình của tam giác $ABC$
Suy ra $MN // BC$ hay $MN // BP$.
Tứ giác $BMNC$ có $MN // BP$ nên tứ giác $BMNC$ là hình thang (đpcm).
b) Vì $N, P$ lần lượt là trung điểm của các cạnh $AC, BC$ nên $NP$ là đường trung bình của tam giác $ABC$
Suy ra $NP // AB$ hay $NP // MB$.
Tứ giác $MNPB$ có $MN // BP; \,BM // NP$ (chứng minh trên).
Do đó, tứ giác $MNPB$ là hình bình hành.
Giải bài 4.8 trang 83 Toán 8 tập 1 KNTT
Cho tam giác $ABC$ có trung tuyến $AM$. Lấy điểm $D$ và $E$ trên cạnh $AB$ sao cho $AD = DE = EB$ và $D$ nằm giữa hai điểm $A, E$.
a) Chứng minh $DC // EM$.
b) $DC$ cắt $AM$ tại $I$. Chứng minh $I$ là trung điểm của $AM$.
Bài giải:
Ta có hình vẽ minh họa sau:
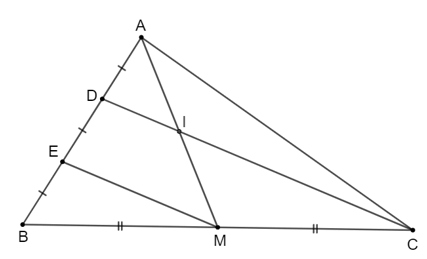
a) Vì $AM$ là đường trung tuyến của tam giác $ABC$ nên $M$ là trung điểm của $BC$.
Ta có:
$BE = DE$ và $E ∈ BD$ nên $E$ là trung điểm của $BD$.
Xét tam giác $BCD$ có $E, M$ lần lượt là trung điểm của $BD, BC$ nên $EM$ là đường trung bình của tam giác $BCD$.
Do đó $DC // EM$ (tính chất đường trung bình).
b) Ta có:
$D$ là trung điểm của $AE$ (vì $AD = DE, \,D ∈ AE$).
Mà $DI // EM$ (vì $DC // EM$).
Do đó $DI$ là đường trung bình của tam giác $AEM$.
Suy ra $I$ là trung điểm của $AM$.
Giải bài 4.9 trang 83 Toán 8 tập 1 KNTT
Cho hình chữ nhật $ABCD$ có $AC$ cắt $BD$ tại $O$. Gọi $H, K$ lần lượt là trung điểm của $AB, AD$. Chứng minh tứ giác $AHOK$ là hình chữ nhật.
Bài giải:
Ta có hình vẽ minh họa sau:
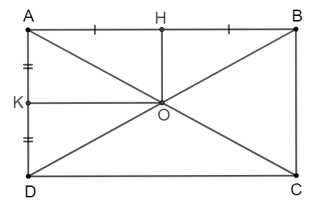
Vì $ABCD$ là hình chữ nhật nên \(\widehat {BA{\rm{D}}} = {90^o}\) và hai đường chéo $AC, BD$ bằng nhau và cắt nhau tại trung điểm $O$ của mỗi đường.
Suy ra $AB ⊥ AD$; $O$ là trung điểm của $AC$ và $BD$.
Vì $O, H$ lần lượt là trung điểm của $BD$ và $AB$ nên $OH$ là đường trung bình của tam giác $ABD$.
Suy ra $OH // AD$ mà $AB ⊥ AD$ nên $OH ⊥ AB$ hay \(\widehat {AHO} = {90^o}\)
Tương tự, ta chứng minh được: $OK ⊥ AD$ hay \(\widehat {AK{\rm{O}}} = {90^o}\).
Ta có:
\(\widehat {BA{\rm{D}}} + \widehat {AHO} + \widehat {AK{\rm{O}}} + \widehat {HOK} = {360^o}\)
$⇔ 90^o+90^o+90^o+\widehat {HOK}=360^o$
$⇔ 270^o+\widehat {HOK}=360^o$
Suy ra $\widehat {HOK}=360^o−270^o=90^o$
Tứ giác $AHOK$ có $\widehat {BAD}=90^o; \,\widehat {AHO}=90^o; \,\widehat {AKO}=90^o; \widehat {HOK}=90^o$
Do đó, tứ giác $AHOK$ là hình chữ nhật.
Bài trước:
👉 Giải bài 1 2 3 4 5 trang 80 sgk Toán 8 tập 1 Kết Nối Tri Thức
Bài tiếp theo:
👉 Giải bài 10 11 12 trang 86 sgk Toán 8 tập 1 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải bài 6 7 8 9 trang 83 sgk Toán 8 tập 1 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
