Nội Dung
Hướng dẫn giải Bài tập cuối chương V sgk Toán 8 tập 1 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
GIẢI BÀI TẬP CUỐI CHƯƠNG V
Sau đây là phần Giải Bài tập cuối chương V trang 109 110 sgk Toán 8 tập 1 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
A. TRẮC NGHIỆM
Giải bài 5.19 trang 109 Toán 8 tập 1 KNTT
Dữ liệu nào sau đây là số liệu liên tục?
A. Dữ liệu về tên các vận động viên Việt Nam tham dự SEA Games 31.
B. Dữ liệu về kết quả đánh giá hiệu quả của chương trình dạy học trên tuyền hình.
C. Dữ liệu về cân nặng của 200 con cá chép sau 6 tháng nuôi.
D. Dữ liệu về số người bị mắc Covid-19 trong gia đình của các bạn trong lớp.
Bài giải:
Ta xét từng dữ liệu đã cho:
• Dữ liệu về tên các vận động viên Việt Nam tham dự SEA Games 31 không là dữ liệu số.
• Dữ liệu về kết quả đánh giá hiệu quả của chương trình dạy học trên tuyền hình không là dữ liệu số.
• Dữ liệu về cân nặng của 200 con cá chép sau 6 tháng nuôi là số liệu liên tục.
• Dữ liệu về số người bị mắc Covid-19 trong gia đình của các bạn trong lớp là số liệu rời rạc.
⇒ Đáp án: C.
Giải bài 5.20 trang 109 Toán 8 tập 1 KNTT
An đứng từ xa và ghi lại xem bạn nào đi sang đường sử dụng cầu vượt khi tan trường. Phương pháp An thu thập dữ liệu là:
A. Từ nguồn có sẵn.
B. Quan sát.
C. Lập bảng hỏi.
D. Phỏng vấn.
Bài giải:
An đứng từ xa và ghi lại xem bạn nào đi sang đường sử dụng cầu vượt khi tan trường.
Trong trường hợp này, An quan sát các bạn đi sang đường sử dụng cầu vượt khi tan trường rồi ghi lại kết quả.
Do đó, phương pháp An thu thập dữ liệu là quan sát.
⇒ Đáp án: B.
Giải bài 5.21 trang 109 Toán 8 tập 1 KNTT
Trong biểu đồ cột với gốc trục đứng không bắt đầu từ 0, khẳng định nào sau đây không đúng?
A. Cột cao hơn biểu diễn số liệu lớn hơn.
B. Hai cột cao bằng nhau biểu diễn số liệu bằng nhau.
C. Cột thấp hơn biểu diễn số liệu bé hơn.
D. Tỉ lệ chiều cao của hai cột bằng tỉ lệ hai số liệu được biểu diễn.
Bài giải:
Trong biểu đồ cột với gốc trục đứng không bắt đầu từ 0 thì tỉ lệ chiều cao của hai cột không bằng tỉ lệ hai số liệu được biểu diễn.
⇒ Đáp án: D.
Giải bài 5.22 trang 109 Toán 8 tập 1 KNTT
Để biểu diễn tỉ lệ của các phần trong tổng thể ta dùng biểu đồ nào sau đây?
A. Biểu đồ tranh.
B. Biểu đồ cột.
C. Biểu đồ đoạn thẳng.
D. Biểu đồ hình quạt tròn.
Bài giải:
Để biểu diễn tỉ lệ của các phần trong tổng thể ta dùng biểu đồ hình quạt tròn.
⇒ Đáp án: D.
Giải bài 5.23 trang 109 Toán 8 tập 1 KNTT
Để biểu diễn sự thay đổi của một đại lượng theo thời gian ta dùng biểu đồ nào sau đây?
A. Biểu đồ cột kép.
B. Biểu đồ tranh.
C. Biểu đồ đoạn thẳng.
D. Biểu đồ hình quạt tròn.
Bài giải:
Để biểu diễn sự thay đổi của một đại lượng theo thời gian ta dùng biểu đồ đoạn thẳng.
⇒ Đáp án: C.
B. TỰ LUẬN
Giải bài 5.24 trang 109 Toán 8 tập 1 KNTT
Cho hai biểu đồ

a) Lập bảng thống kê cho dữ liệu được biểu diễn trong mỗi biểu đồ.
b) Dữ liệu biểu diễn trên hai biểu đồ có như nhau không? Giải thích tại sao hình dạng hai đường gấp khúc trên hai biểu đồ lại khác nhau.
Bài giải:
a) Bảng thống kê dữ liệu biểu diễn trên biểu đồ a):
| Tháng | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Số sản phẩm (nghìn) | 3 | 2 | 3 | 4 | 5 | 4 | 6 | 7 | 8 | 7 | 6 | 8 |
Bảng thống kê dữ liệu biểu diễn trên biểu đồ b):
| Tháng | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Số sản phẩm (nghìn) | 3 | 2 | 3 | 4 | 5 | 4 | 6 | 7 | 8 | 7 | 6 | 8 |
b) Dữ liệu biểu diễn trên hai biểu đồ là như nhau.
Hình dạng đường gấp khúc ở hai biểu đồ khác nhau do trục đứng của hai biểu đồ chia theo tỉ lệ khác nhau.
Giải bài 5.25 trang 110 Toán 8 tập 1 KNTT
Khối 8 tổ chức giải bóng đá với 5 đội tham dự là các đội bóng của các lớp A, B, C, D, E. Trước khi giải đấu diễn ra, Bình muốn thực hiện khảo sát dự đoán của các bạn về đội vô địch giải đấu.
a) Theo em Bình có thể thực hiện khảo sát theo những cách nào?
b) Dữ liệu Bình thu được thuộc loại nào?
Bài giải:
a) Cách Bình có thể thực hiện khảo sát: phỏng vấn, lập bảng hỏi.
b) Dữ liệu không là số không thể sắp thứ tự.
Giải bài 5.26 trang 110 Toán 8 tập 1 KNTT
Bạn Bình tiến hành khảo sát dự đoán như trong bài 5.25. Giả sử Bình thu được kết quả như sau: A, B, A, A, A, A, A, B, D, B, A, A, B, D, D, A, A, B, D. Lập bảng thống kê về số lượng dự đoán vô địch cho mỗi đội
a) Có thể dùng biểu đồ nào để biểu diễn dữ iệu trong bảng thống kê thu được
b) Nếu muốn biểu diễn tỉ lệ các bạn được hỏi dự đoán mỗi đội vô địch thì nên dùng biểu đồ nào?
Bài giải:
Bảng thống kê:
| Đội | A | B | C | D | E |
| Số lượng | 10 | 5 | 0 | 4 | 0 |
a) Có thể dùng biểu đồ tranh hoặc biểu đồ cột để biểu diễn dữ liệu trong bảng thống kê thu được.
b) Biểu đồ hình quạt tròn dùng để biểu diễn tỉ lệ của các phần trong tổng thể.
Do đó, nếu muốn biểu diễn tỉ lệ các bạn được hỏi dự đoán mỗi đội vô địch thì nên dùng biểu đồ hình quạt tròn.
Giải bài 5.27 trang 110 Toán 8 tập 1 KNTT
Bảng thống kê sau cho biết số lượng học sinh của các lớp khối 8 tham gia các câu lạc bộ Thể thao và Nghệ thuật của trường.
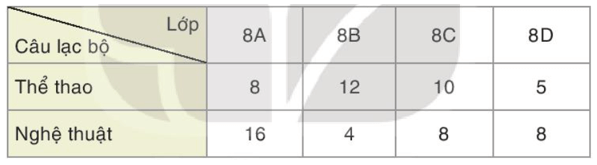
a) Lựa chọn và vẽ biểu đồ để so sánh số lượng học sinh tham gia hai câu lạc bộ này ở từng lớp.
b) Lựa chọn và vẽ biểu đồ biểu diễn tỉ lệ học sinh các lớp tham gia hai câu lạc bộ trong số các học sinh khối 8 tham gia hai câu lạc bộ này.
Bài giải:
a) Để so sánh số lượng học sinh tham gia hai câu lạc bộ này ở từng lớp, ta chọn biểu đồ cột kép.
Biểu đồ cột kép biểu diễn số lượng của các lớp khối 8 tham gia các câu lạc bộ Thể thao và Nghệ thuật của trường như sau:

b) Để biểu diễn tỉ lệ học sinh các lớp tham gia hai câu lạc bộ trong số các học sinh khối 8 tham gia hai câu lạc bộ này ta dùng biểu đồ hình quạt tròn.
Tổng số học sinh tham gia hai câu lạc bộ của khối 8 là:
8 + 16 + 12 + 4 + 10 + 8 + 5 + 8 = 71 (học sinh).
• Tổng số học sinh tham gia hai câu lạc bộ của lớp 8A là: 8 + 16 = 24 (học sinh).
Tỉ số phần trăm số học sinh tham gia hai câu lạc bộ của lớp 8A so với số các học sinh khối 8 tham gia hai câu lạc bộ là: \(\frac{{24}}{{71}} \approx 33,8\% \).
• Tổng số học sinh tham gia hai câu lạc bộ của lớp 8B là: 12 + 4 = 16 (học sinh).
Tỉ số phần trăm số học sinh tham gia hai câu lạc bộ của lớp 8B so với số các học sinh khối 8 tham gia hai câu lạc bộ là: \(\frac{{16}}{{71}} \approx 22,5\% \).
• Tổng số học sinh tham gia hai câu lạc bộ của lớp 8C là: 10 + 8 = 18 (học sinh).
Tỉ số phần trăm số học sinh tham gia hai câu lạc bộ của lớp 8C so với số các học sinh khối 8 tham gia hai câu lạc bộ là: \(\frac{{18}}{{71}} \approx 25,4\% \).
• Tỉ số phần trăm số học sinh tham gia hai câu lạc bộ của lớp 8C so với số các học sinh khối 8 tham gia hai câu lạc bộ là:
100% − 33,8% − 22,5% − 25,4% = 18,3%.
Biểu đồ hình quạt tròn biểu diễn tỉ lệ học sinh các lớp tham gia hai câu lạc bộ trong số các học sinh khối 8 tham gia hai câu lạc bộ này.
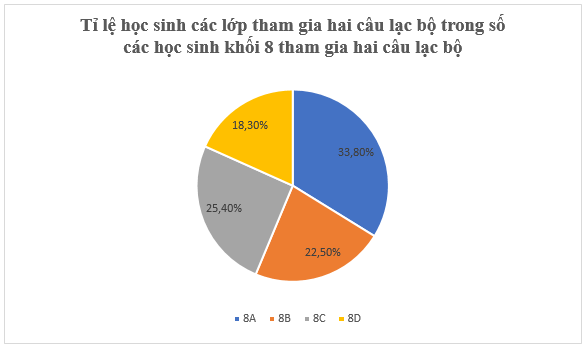
Bài trước:
👉 Giải bài 15 16 17 18 trang 108 sgk Toán 8 tập 1 Kết Nối Tri Thức
Bài tiếp theo:
👉 HĐTH&TN: Công thức lãi kép sgk Toán 8 tập 1 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn Giải Bài tập cuối chương V trang 109 110 sgk Toán 8 tập 1 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“
