Nội Dung
Hướng dẫn giải Bài Hoạt động thực hành và trải nghiệm sgk Toán 8 tập 1 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài HĐTH&TN: Thực hiện tính toán trên đa thức với phần mềm GeoGebra sgk Toán 8 tập 1 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 8.
THỰC HIỆN TÍNH TOÁN TRÊN ĐA THỨC VỚI PHẦN MỀM GEOGEBRA
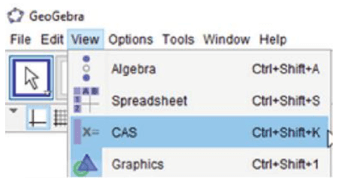
Khởi động phần mềm GeoGebra 
, chọn View → Complex Adaptive System (CAS) để thực hiện tính toán các phép tính trên đa thức.
1. Cộng, trừ, nhân đa thức: Nhập biểu thức trên dòng lệnh của cửa sổ CAS, kết quả sẽ được hiển thị ngay bên dưới.
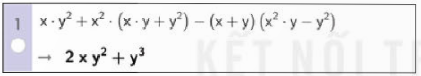
2. Khai triển các biểu thức có chứa tích hoặc lũy thừa: Sử dụng lệnh Expand(<biểu thức cần khai triển>).
3. Phân tích đa thức thành nhân tử: Sử dụng lệnh Factor(<đa thức>) (hoặc Factor(<đa thức>)).
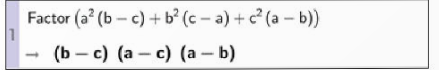
Trường hợp phân tích đa thức thành nhân tử có chứa số vô tỉ thì dùng lệnh Ifactor(<đa thức>).
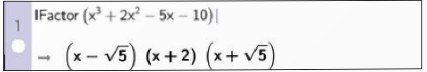
4. Chia đa thức: Dùng lệnh Div(<đa thức bị chia>, <đa thức chia>) để tìm thương; lệnh Mod(<đa thức bị chia>, <đa thức chia>) để tìm dư; lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
Thực hành
Giải bài 1 trang 114 Toán 8 tập 1 KNTT
Tính:
\(\left( {3{x^2}y + 5xy – 2} \right)\left( {4x + 3y} \right) – 6{x^2}\left( {2xy + \frac{3}{2}{y^2} + \frac{{10}}{3}y} \right)\).
Bài giải:
Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
Giải bài 2 trang 114 Toán 8 tập 1 KNTT
Khai triển các biểu thức sau:
a) ${\left( {5x – y} \right)^2}$;
b) ${\left( {\frac{1}{2}x + 2y} \right)^3}$.
Bài giải:
a) Khai triển biểu thức \({\left( {5x – y} \right)^2}\):
• Sử dụng lệnh Expand(<biểu thức cần khai triển>).
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
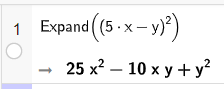
Vậy \({\left( {5x – y} \right)^2} = 25{x^2} – 10xy + {y^2}\).
b) Khai triển biểu thức: \({\left( {\frac{1}{3}x + 2y} \right)^3}\):
• Sử dụng lệnh Expand(<biểu thức cần khai triển>).
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
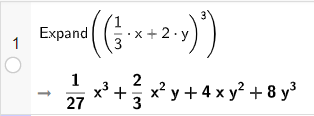
Vậy \({\left( {\frac{1}{3}x + 2y} \right)^3} = \frac{1}{{27}}{x^3} + \frac{2}{3}{x^2}y + 4x{y^2} + 8{y^3}\).
Giải bài 3 trang 114 Toán 8 tập 1 KNTT
Phân tích các đa thức sau thành nhân tử:
a) ${x^4} – 4{x^3} – 7{x^2} + 8x + 10$;
b) ${\left( {x + y + z} \right)^3} – {x^3} – {y^3} – {z^3}$.
Bài giải:
a) Phân tích các đa thức \({x^4} – 4{x^3} – 7{x^2} + 8x + 10\) thành nhân tử:
• Sử dụng lệnh Factor(<đa thức>) (hoặc Factorise(<đa thức>)).
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
Vậy \({x^4} – 4{x^3} – 7{x^2} + 8x + 10 = \left( {x – 5} \right)\left( {x + 1} \right)\left( {{x^2} – 2} \right)\).
b) Phân tích các đa thức \({\left( {x + y + z} \right)^3} – {x^3} – {y^3} – {z^3}\) thành nhân tử:
• Sử dụng lệnh Factor(<đa thức>) (hoặc Factorise(<đa thức>)).
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
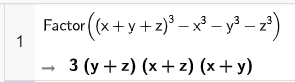
Vậy \({\left( {x + y + z} \right)^3} – {x^3} – {y^3} – {z^3} = 3\left( {y + z} \right)\left( {x + z} \right)\left( {x + y} \right)\).
Giải bài 4 trang 114 Toán 8 tập 1 KNTT
Tìm thương và dư (nếu có) trong các phép chia sau:
a) $\left( {3{x^4}y – 9{x^3}{y^2} – 21{x^2}{y^2}} \right):\left( {3{x^2}y} \right)$;
b) $\left( {2{x^3} + 5{x^2} – 2x + 12} \right):\left( {2{x^2} – x + 1} \right)$.
Bài giải:
a) Tìm thương và dư (nếu có) trong các phép chia \(\left( {3{x^4}y – 9{x^3}{y^2} – 21{x^2}{y^2}} \right):\left( {3{x^2}y} \right)\):
• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
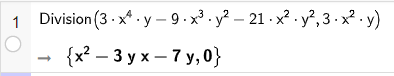
Vậy phép chia hai đa thức \(\left( {3{x^4}y – 9{x^3}{y^2} – 21{x^2}{y^2}} \right)\) cho \(3{x^2}y\), ta được thương là \({x^2} – 3xy – 7y\) và dư $0$.
b) Tìm thương và dư (nếu có) trong các phép chia $(2x^3 + 5x^2 – 2x + 12) : (2x^2 – x + 1)$.
• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
Vậy phép chia hai đa thức $(2x^3 + 5x^2 – 2x + 12)$ cho $(2x^2 – x + 1)$, ta được thương là $x + 3$ và dư $9$.
Bài trước:
👉 HĐTH&TN: Công thức lãi kép sgk Toán 8 tập 1 Kết Nối Tri Thức
Bài tiếp theo:
👉 HĐTH&TN: Vẽ hình đơn giản với phần mềm GeoGebra sgk Toán 8 tập 1 Kết Nối Tri Thức KNTT
Trên đây là bài Hướng dẫn HĐTH&TN: Thực hiện tính toán trên đa thức với phần mềm GeoGebra sgk Toán 8 tập 1 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 8 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“