Nội Dung
Hướng dẫn giải Bài Hoạt động thực hành và trải nghiệm sgk Toán 7 tập 1 bộ Kết Nối Tri Thức Với Cuộc Sống. Nội dung bài HĐTH&TN: Vẽ hình đơn giản với phần mềm GeoGebra Toán 7 tập 1 Kết Nối Tri Thức bao gồm đầy đủ phần lí thuyết kèm bài giải các câu hỏi, hoạt động, luyện tập, vận dụng và bài tập, giúp các bạn học sinh học tốt môn toán 7.
VẼ HÌNH ĐƠN GIẢN VỚI PHẦN MỀM GEOGEBRA
HĐ1 VẼ HAI ĐƯỜNG THẲNG SONG SONG
Hoạt động 1 trang 110 Toán 7 tập 1 KNTT
Em thấy vẽ hai đường thẳng song song bằng bút và thước kẻ thật khó đúng không. Chúng ta sẽ sử dụng hộp công cụ đường thẳng trong Geogebra để vẽ nhé.
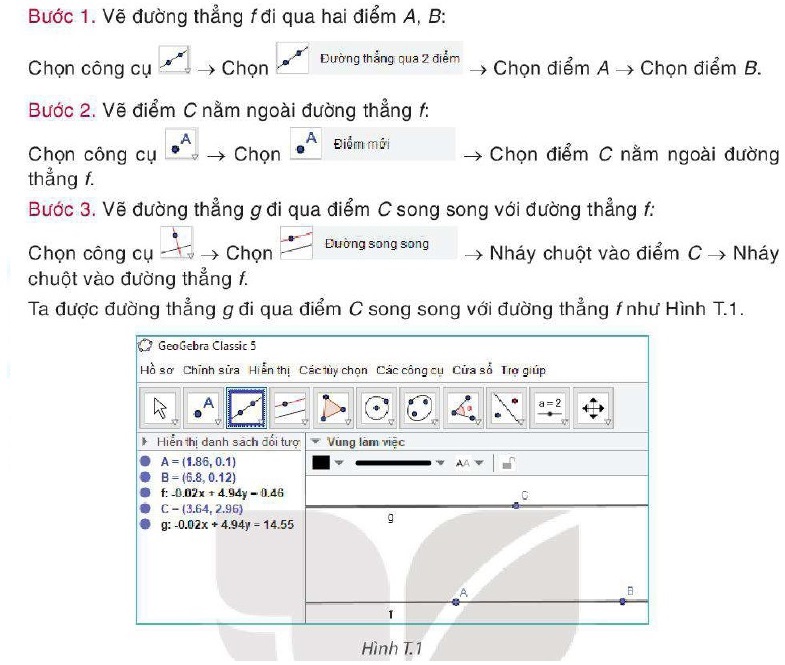
Cùng suy luận trang 111 Toán 7 tập 1 KNTT
Sau khi thực hiện Bước 3, ta thấy có đúng một đường thẳng g được hiện ra. Điều này gợi cho em liên tưởng đến khẳng định nào?
Trả lời:
Ta liên tưởng tới Tiên đề Euclid: “Qua một điểm nằm ngoài một đường thẳng, chỉ có duy nhất một đường thẳng song song với đường thẳng đã cho”.
HĐ2 VẼ TIA PHÂN GIÁC CỦA MỘT GÓC
Hoạt động 2 trang 111 Toán 7 tập 1 KNTT
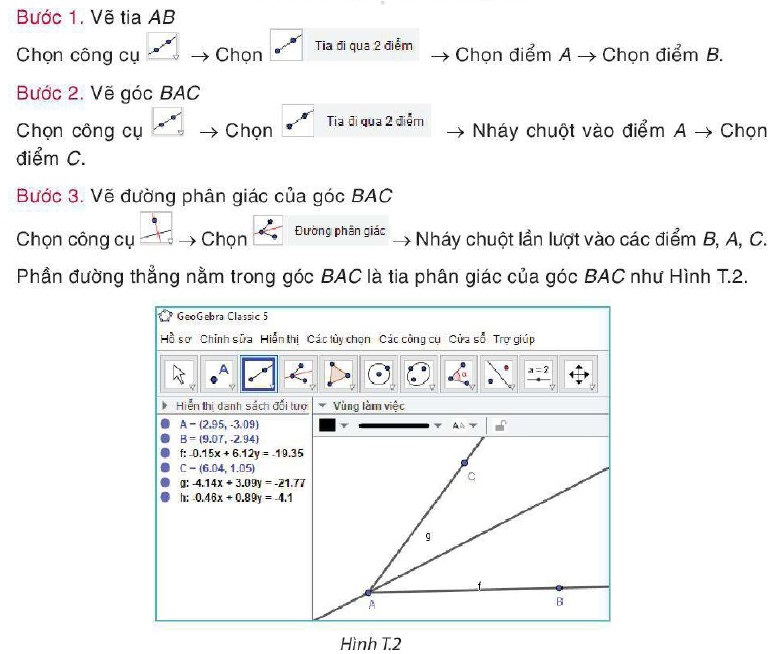
Các em vẽ tia phân giác của góc BAC theo các bước sau:
HĐ3 VẼ ĐƯỜNG TRUNG TRỰC CỦA MỘT ĐOẠN THẲNG
Hoạt động 3 trang 112 Toán 7 tập 1 KNTT
Các em vẽ đường trung trực của đoạn thẳng AB theo các bước sau:
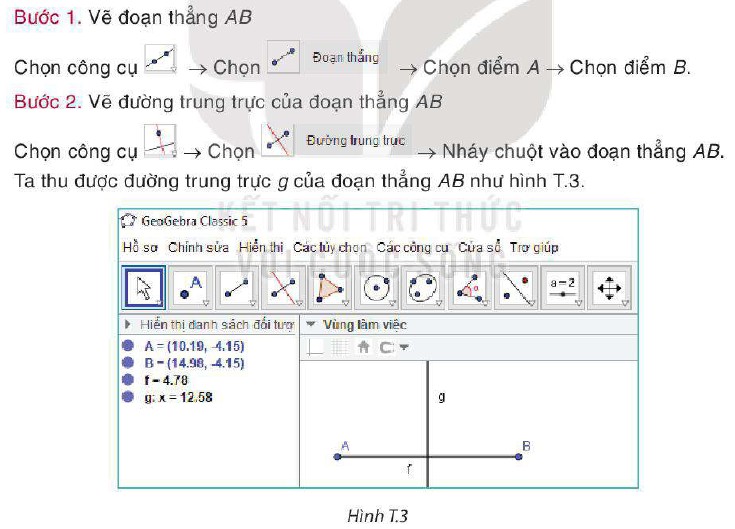
Cùng suy luận trang 111 Toán 7 tập 1 KNTT
Cùng suy luận. Bạn Lan vẽ đường trung trực của đoạn thẳng AB theo các bước sau:
Đường thẳng g vẽ được có phải là đường trung trực của đoạn thẳng AB không?
Trả lời:
Bạn Lan vẽ được hình như sau:
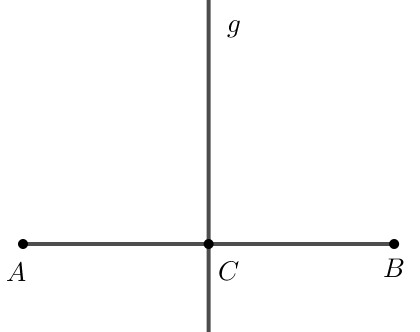
⇒ Đường thẳng g là đường trung trực của đoạn thẳng AB vì g vuông góc với AB tại trung điểm C của AB.
HĐ4 VẼ TAM GIÁC BIẾT ĐỘ DÀI BA CẠNH
Hoạt động 4 trang 113 Toán 7 tập 1 KNTT
Các em vẽ tam giác ABC có AB = 4 cm, BC = 5 cm, CA = 6 cm theo các bước sau:
Câu hỏi trang 113 Toán 7 tập 1 KNTT
Nếu cho trước đoạn thẳng AB = 4 cm cố định. Em vẽ được mấy tam giác ABC thỏa mãn yêu cầu BC = 5 cm, CA = 6 cm?
Trả lời:
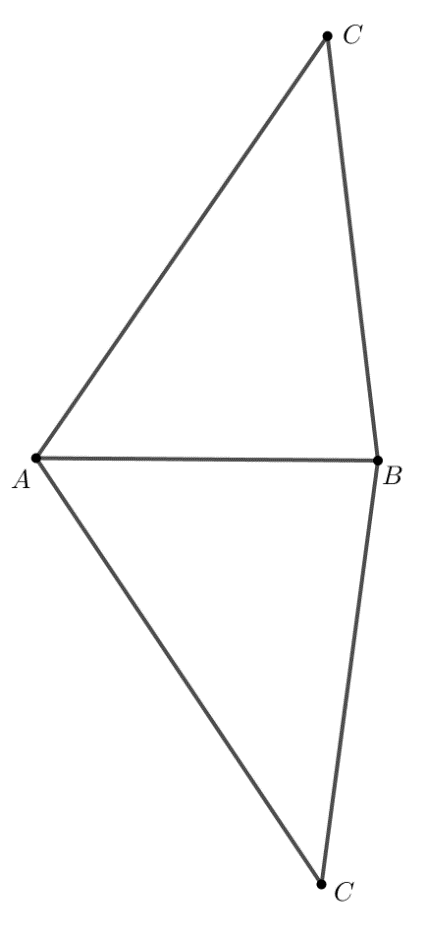
Thực hiện tương tự như các bước trong Hoạt động 4, ở bước số 4 khi lấy giao điểm của hai đường tròn, ta thấy hai đường tròn này giao nhau tại hai điểm. Do đó ngoài lấy điểm C như Hoạt động 4 thì ta có thể chọn điểm C ở bên dưới.
Vì vậy ta có thể vẽ được hai tam giác ABC thỏa mãn yêu cầu BC = 5 cm, CA = 6 cm.
Hình vẽ dưới đây minh họa hai vị trí của điểm C thỏa mãn yêu cầu của đề bài:
HĐ5 VẼ TAM GIÁC BIẾT ĐỘ DÀI HAI CẠNH VÀ GÓC XEN GIỮA
Hoạt động 5 trang 114 Toán 7 tập 1 KNTT
Câu hỏi trang 114 Toán 7 tập 1 KNTT
Tam giác ABC có phải là tam giác nhọn không? Em hãy sử dụng công cụ 
kiểm tra các góc của tam giác để trả lời câu hỏi đó.
Trả lời:
Sử dụng công cụ ta đo được số đo của các góc như sau:
Để đo góc ABC, ta làm như sau:
– Nhấn biểu tượng → Chọn 
→ sau đó nhấn lần lượt các điểm C, B, A; ta được số đo góc CAB là 51,050.
Để đo góc ACB, ta làm như sau:
– Nhấn biểu tượng → Chọn → sau đó nhấn lần lượt các điểm A, C, B; ta được số đo góc ACB là 68,950.
Ta có hình vẽ sau:
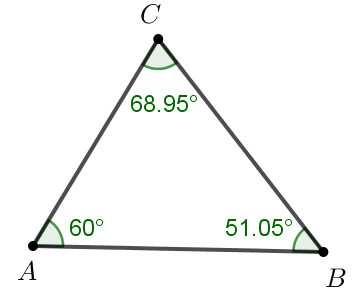
Ta thấy Tam giác ABC có 3 góc đều nhỏ hơn 90 độ nên tam giác ABC là tam giác nhọn.
Luyện tập 1 trang 114 Toán 7 tập 1 KNTT
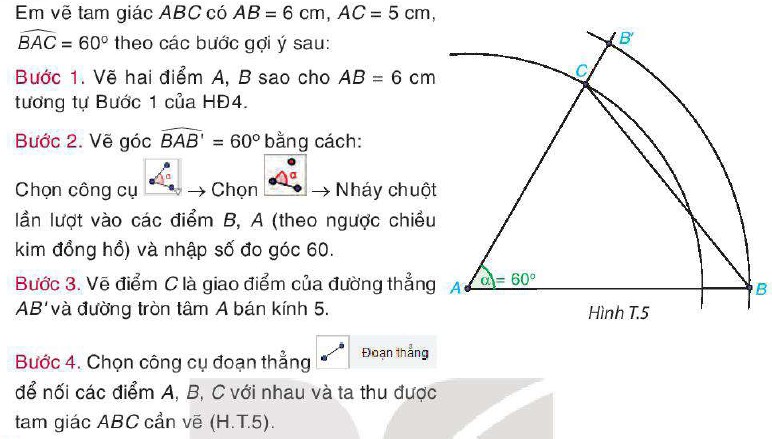
Vẽ tam giác ABC có AB = 6 cm, \(\widehat {BAC} = 50^\circ ;\widehat {ABC} = 60^\circ \).
Gợi ý: Vẽ \(\widehat {BAB’} = 50^\circ \) theo chiều ngược chiều kim đồng hồ; \(\widehat {ABA’} = 60^\circ \) (theo chiều kim đồng hồ) và C là giao điểm của 2 tia AB’ và BA’.
Trả lời:
Ta thực hiện theo các bước sau:
Bước 1. Vẽ hai điểm A, B sao cho AB = 6 cm tương tự như Bước 1 của Hoạt động 5.
Bước 2. Vẽ \(\widehat {BAB’} = 50^\circ \) bằng cách:
Chọn công cụ → Chọn 
→ Nháy chuột lần lượt vào điểm B, A (theo ngược chiều kim đồng hồ) và nhập số đo góc 50.
Bước 3. Vẽ \(\widehat {ABA’} = 60^\circ \) bằng cách:
Chọn công cụ → Chọn → Nháy chuột lần lượt vào điểm A, B (theo chiều kim đồng hồ) và nhập số đo góc 60.
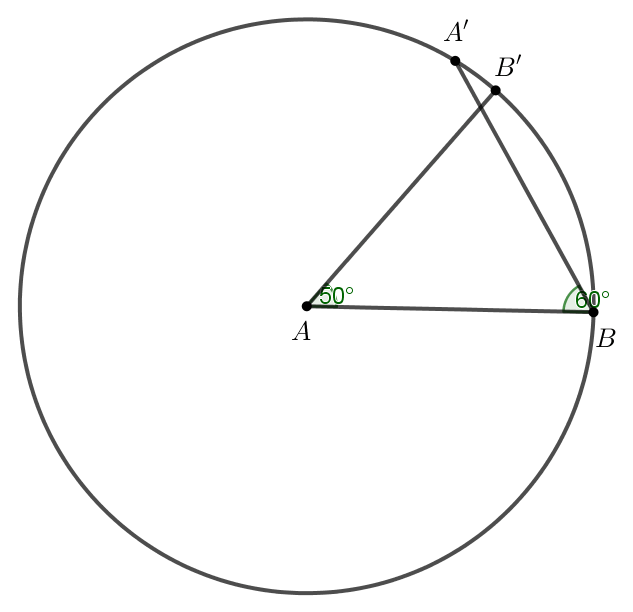
Bước 4. Xác định điểm C bằng cách:
Chọn công cụ 
→ Chọn 
→ Lần lượt nháy chuột vào hai đường thẳng AB’ và BA’ ta được điểm C.
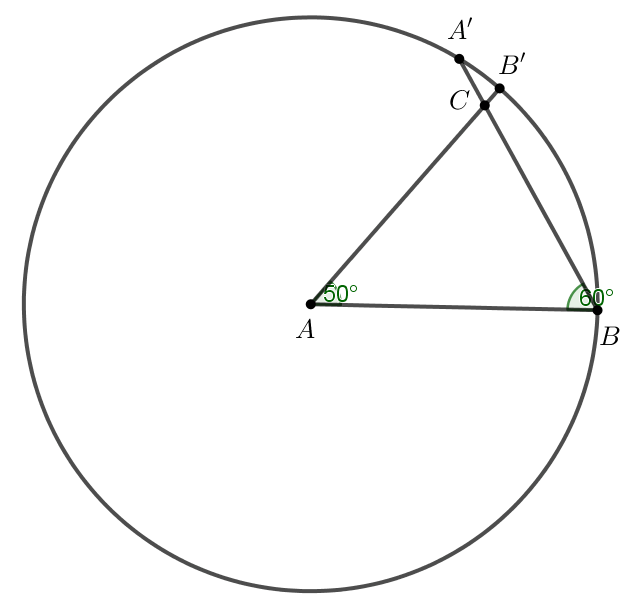
Bước 5. Ẩn đường tròn, ẩn các đoạn AB’, BA’ và ẩn các điểm A’, B’.
Chọn công cụ đoạn thẳng 
để nối các điểm A, B, C với nhau và ta thu được tam giác ABC.
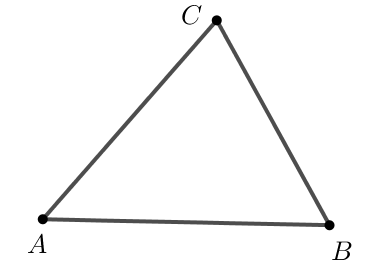
Luyện tập 2 trang 114 Toán 7 tập 1 KNTT
Vẽ tam giác ABC vuông tại A, AB = 4 cm, BC = 6 cm.
Gợi ý:
– Vẽ đoạn thẳng AB = 4 cm.
– Vẽ C là giao điểm của đường tròn tâm B bán kính 6 và đường thẳng đi qua A vuông góc với AB.
Trả lời:
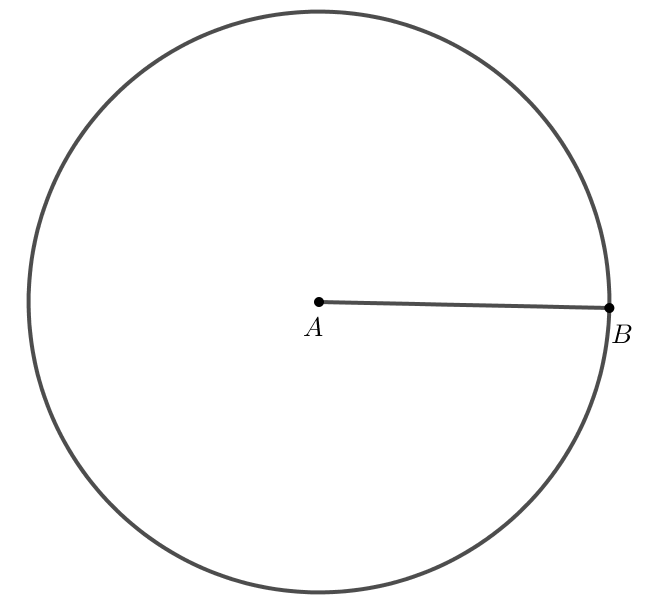
Bước 1. Thực hiện vẽ hai điểm A, B sao cho AB = 4 cm.
Bước 2. Vẽ đường thẳng qua A vuông góc với AB:
Chọn công cụ 
→ Chọn 
→ Nháy chuột lần lượt vào điểm A và đoạn thẳng AB.
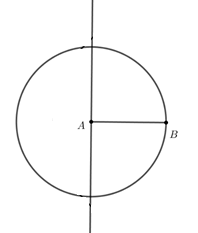
Bước 3. Vẽ đường tròn tâm B bán kính 6:
Chọn công cụ 
→ Chọn 
→ Chọn điểm B, nhập bán kính bằng 6.
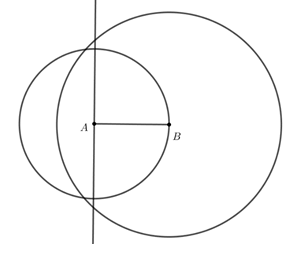
Bước 4. Chọn công cụ → Chọn → Lần lượt nháy chuột vào đường thẳng và đường tròn vừa vẽ ở Bước 2, điểm C là điểm được đánh dấu.
Ta sẽ tìm được 2 điểm C, chọn 1 trong 2 điểm đó.
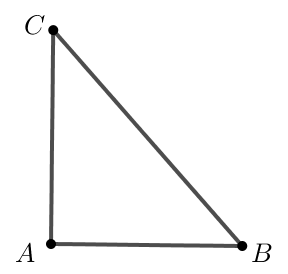
Bước 4. Ẩn các đường thẳng, đường tròn, sau đó sử dụng công cụ đoạn thẳng để nối các điểm A, B, C ta thu được tam giác ABC.
GIẢI BÀI TẬP
Sau đây là phần Giải bài tập 1 2 trang 114 sgk Toán 7 tập 1 Kết Nối Tri Thức. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
Giải bài 1 trang 114 Toán 7 tập 1 KNTT
a) Em hãy trình bày các bước dùng phần mềm Geogebra để vẽ tam giác ABC có: AB = 6 cm, \(\widehat {BAC} = 60^\circ ;\widehat {ACB} = 70^\circ \).
b) Vẽ tam giác trên trong phần mềm Geogebra và lưu thành một tệp có đuôi png.
Bài giải:
a) Ta thực hiện theo các bước như sau:
Bước 1. Vẽ hai điểm A, B sao cho đoạn thẳng AB = 6 cm.
Bước 2. Tính được góc \(\widehat {ABC} = 180^\circ – 60^\circ – 70^\circ = 50^\circ\) (định lý tổng ba góc trong tam giác)
Vẽ góc \(\widehat {BAC} = 60^\circ \) bằng cách:
Chọn công cụ → Chọn → Nháy chuột lần lượt vào điểm B, A (theo ngược chiều kim đồng hồ) và nhập số đo góc 60.
Vẽ góc \(\widehat {ABA’} = 50^\circ \) bằng cách:
Chọn công cụ → Chọn → Nháy chuột lần lượt vào điểm A, B (theo chiều kim đồng hồ) và nhập số đo góc 50.
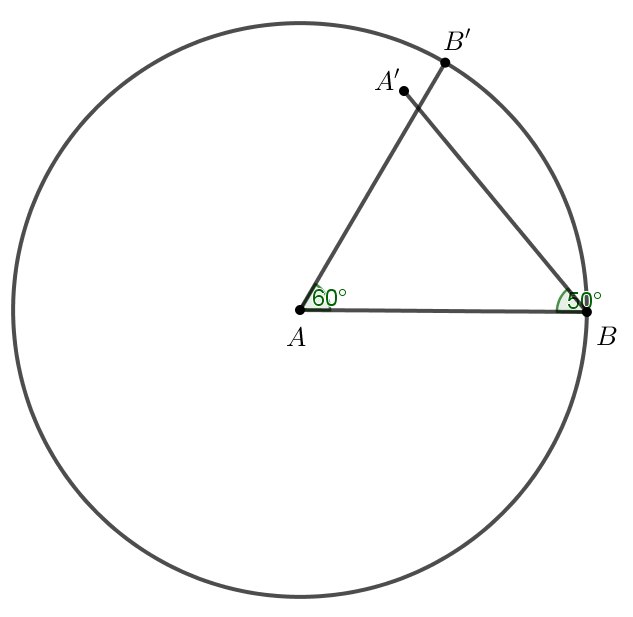
Bước 3. Xác định điểm C bằng cách:
Chọn công cụ → Chọn → Lần lượt nháy chuột vào hai đường thẳng AB’ và BA’ ta được điểm C.
Bước 4. Ẩn các đoạn thẳng AB’, BA’ và đường tròn.
Sau đó sử dụng công cụ đoạn thẳng để nối các điểm A, B, C ta thu được tam giác ABC.
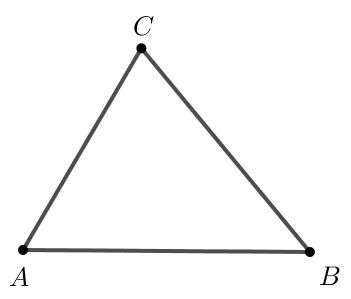
b) Để lưu thành tệp có đuôi png ta thực hiện theo các bước như sau:
Bước 1. Trên thanh công cụ, chọn “Hồ sơ” → “Xuất bản” → “Hiển thị đồ thị dạng hình (png, eps, …)”
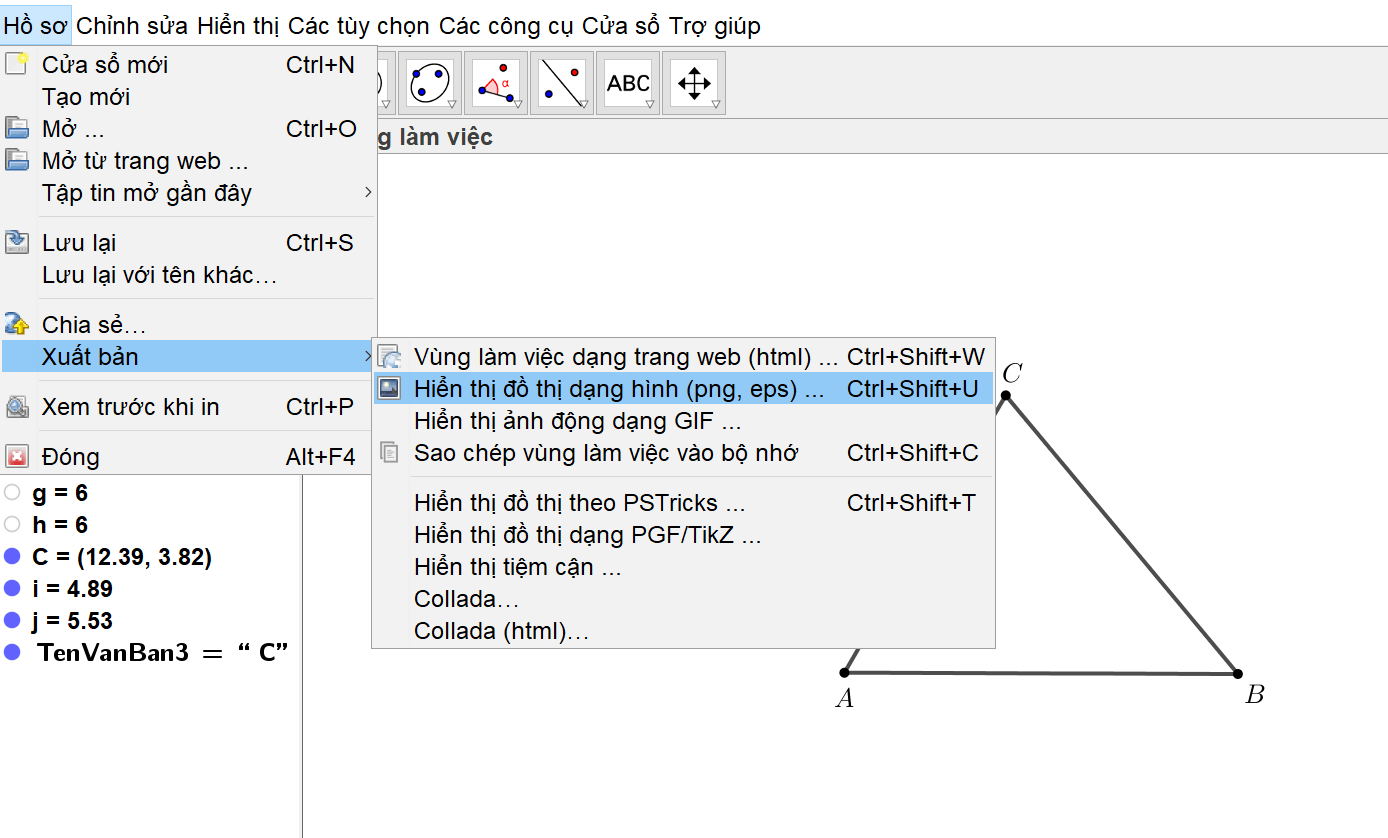
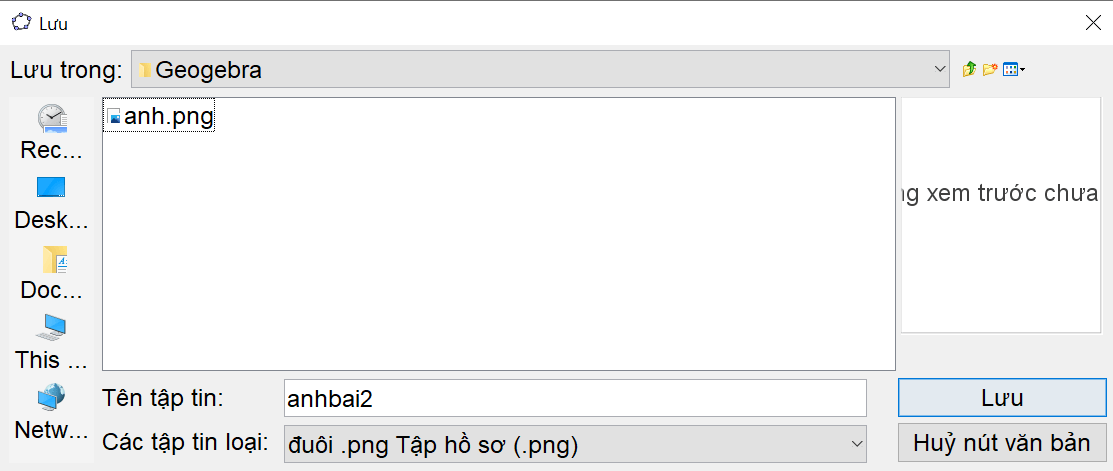
Bước 2. Xuất hiện hộp thoại như bên dưới, chọn “Lưu lại”.
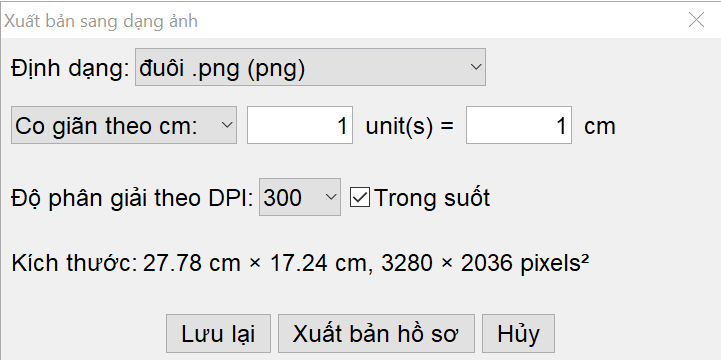
Bước 3. Chọn thư mục lưu trữ, nhập tên file muốn lưu, sau đó ấn “Lưu”.
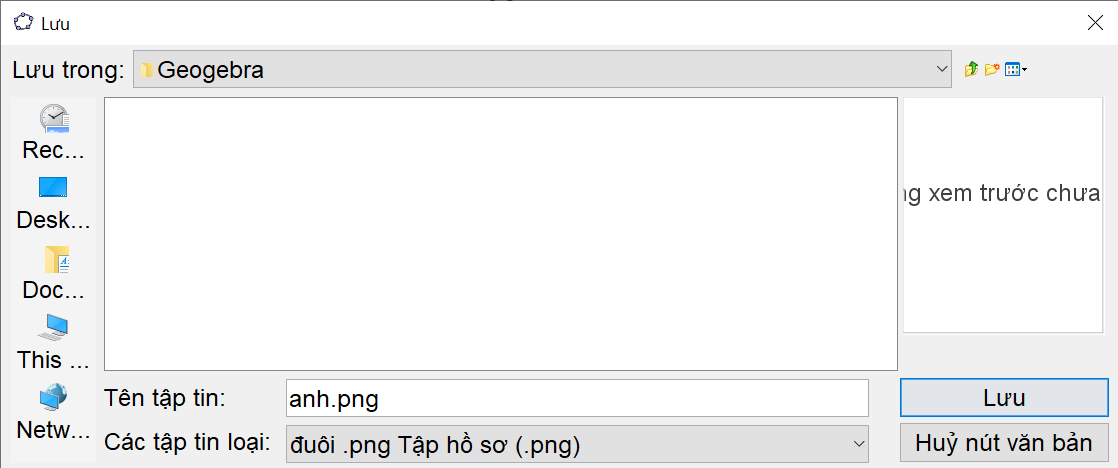
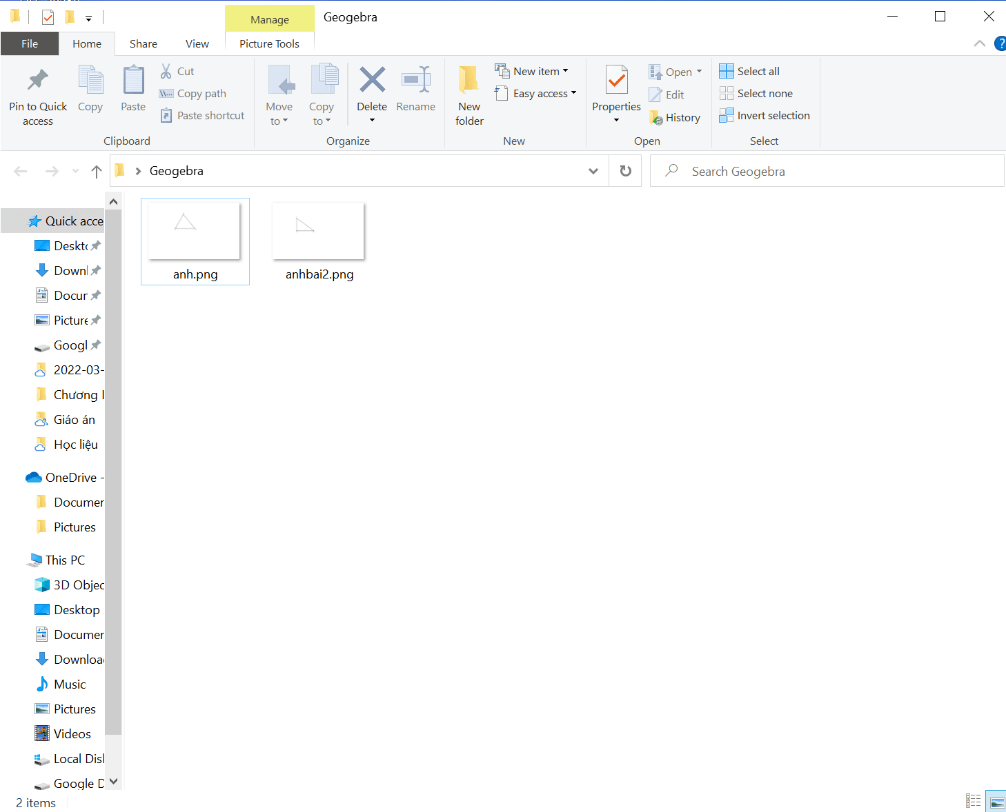
Bước 4. Mở thư mục lưu trữ, kiểm tra file vừa lưu, ta được kết quả như sau:
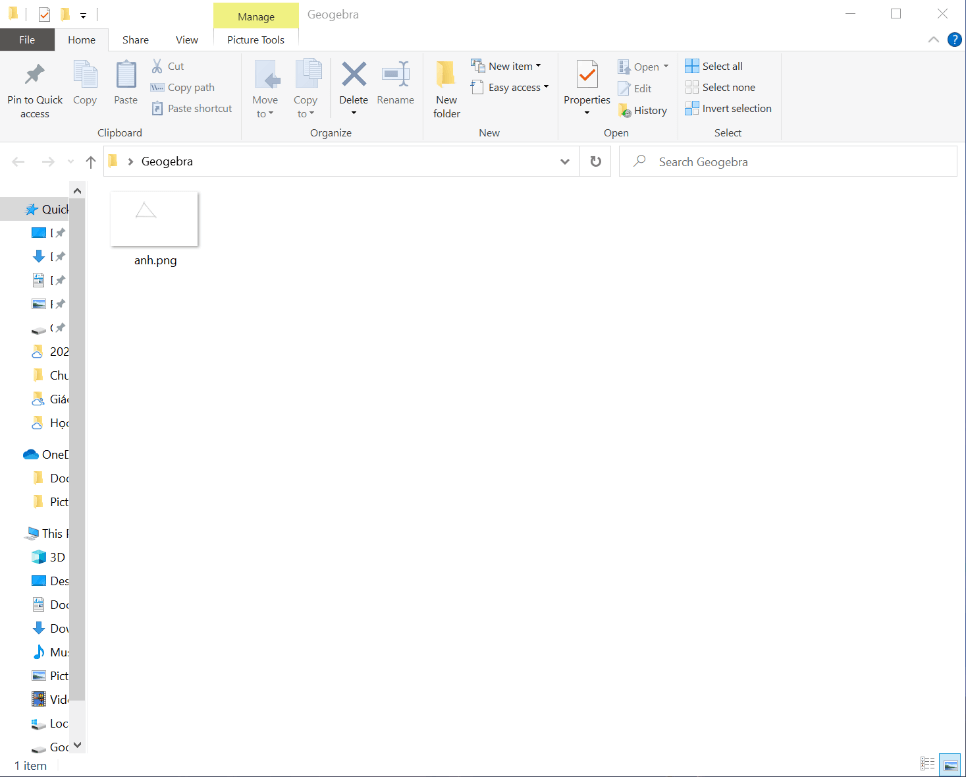
Giải bài 2 trang 114 Toán 7 tập 1 KNTT
a) Sử dụng phần mềm Geogebra, em hãy vẽ tam giác ABC vuông tại A, AB = 4 cm, AC = 3 cm và lưu thành một tệp có đuôi png.
b) Dùng phần mềm Geogebra, em hãy đo độ dài cạnh BC.
Bài giải:
a) Ta thực hiện theo các bước như sau:
Bước 1. Vẽ hai điểm A, B sao cho AB = 4 cm.
Chọn công cụ → Chọn → Nháy chuột lần lượt vào điểm A và đoạn thẳng AB.
Vẽ đường tròn tâm A bán kính 3 cm.
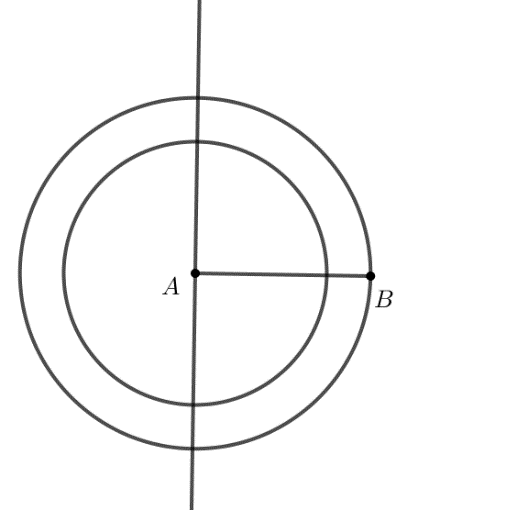
Bước 3. Xác định điểm C bằng cách:
Bước 4. Chọn công cụ → Chọn → Lần lượt nháy chuột vào đường thẳng đi qua A vuông góc với AB và đường tròn tâm A bán kính 3 cm, điểm đánh dấu là điểm C.
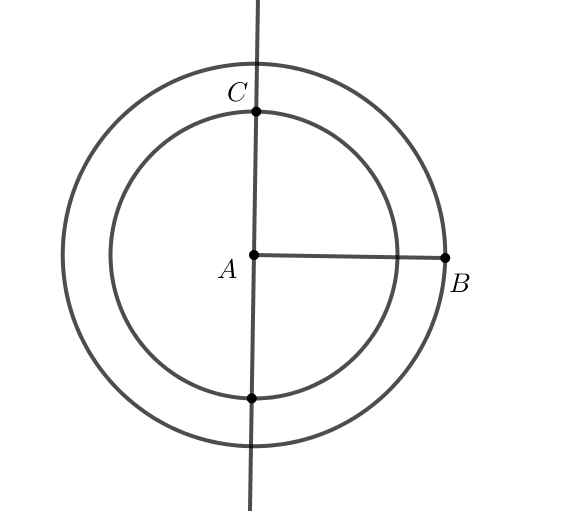
Bước 4. Ẩn các đường thẳng, đường tròn, sau đó sử dụng công cụ đoạn thẳng 
để nối các điểm A, B, C ta thu tam giác ABC.
Để lưu file thành tệp có đuôi png ta thực hiện như sau:
Bước 1. Trên thanh công cụ, chọn “Hồ sơ” → “Xuất bản” → “Hiển thị đồ thị dạng hình (png, eps) …”
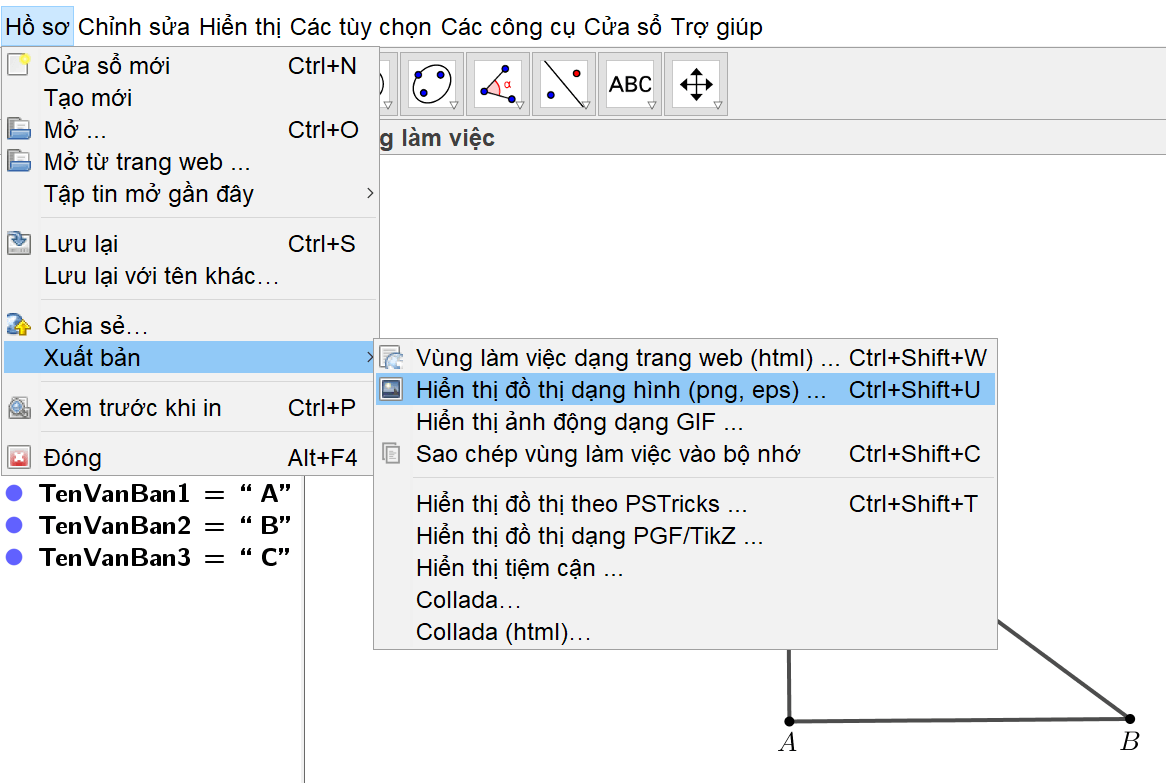
Bước 2. Xuất hiện hộp thoại như bên dưới, chọn “Lưu lại”.
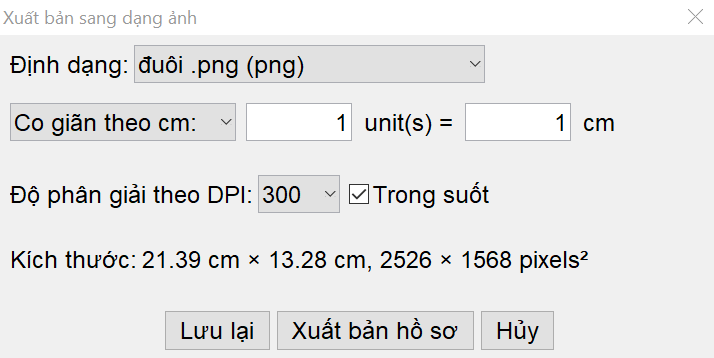
Bước 3. Chọn thư mục lưu trữ, nhập tên file muốn lưu, sau đó ấn “Lưu”.
Bước 4. Mở thư mục lưu trữ, kiểm tra file vừa lưu, ta được kết quả như sau:
b) Để đo độ dài cạnh BC ta thực hiện theo như sau:
Chọn công cụ → Chọn 
→ Nháy chọn lần lượt vào hai điểm B, C.
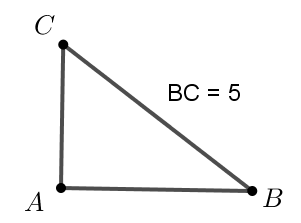
Ta đo được BC = 5 cm.
Bài trước:
👉 Giải bài 18 19 20 21 trang 108 109 sgk Toán 7 tập 1 Kết Nối Tri Thức
Bài tiếp theo:
👉 HĐTH&TN: Dân số và cơ cấu dân số Việt Nam Toán 7 tập 1 Kết Nối Tri Thức
Trên đây là bài Hướng dẫn HĐTH&TN: Vẽ hình đơn giản với phần mềm GeoGebra Toán 7 tập 1 Kết Nối Tri Thức đầy đủ, ngắn gọn và dễ hiểu nhất. Chúc các bạn làm bài môn toán 7 tốt nhất!
“Bài tập nào khó đã có giaibaisgk.com“