Luyện tập bài §9: Giải bài 63 64 65 66 trang 34 sgk Toán 6 tập 2

Nội Dung

Luyện tập bài §9. Phép trừ phân số, sách giáo khoa toán lớp 6. Nội dung giải bài luyện tập: giải bài 63 64 65 66 trang 34 sgk toán 6 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần số học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 6.

Lý thuyết

Bài học sẽ giúp các em đi tìm hiểu các vấn đề liên quan đến phép trừ phân số, các tính chất cùng các dạng toán liên quan và các ví dụ minh họa có hướng dẫn giải sẽ giúp các em dễ dàng nắm được nội dung bài học.

1. Số đối

Định nghĩa: Hai số gọi là đối nhau nếu tổng của chúng bằng 0.

Số đối của phân số \(\frac{a}{b}\) được kí hiệu là \(-\frac{a}{b}.\)

Số đối của phân số \(\frac{a}{b}\) là \(-\frac{a}{b}\) vì \(\frac{a}{b}+\left (-\frac{a}{b} \right )=0\). Như vậy

\(\frac{a}{b}+\left (-\frac{a}{b} \right )=0\) và \(-\frac{a}{b}=\frac{-a}{b}=\frac{a}{-b}.\)

2. Phép trừ phân số

Quy tắc: Muốn trừ một phân số cho một phân số, ta cộng số bị trừ với số đối của số trừ.

\(\frac{a}{b}-\frac{c}{d}=\frac{a}{b}+\left (-\frac{c}{d} \right ).\)

Kết quả của phép trừ \(\frac{a}{b}-\frac{c}{d}\) được gọi là hiệu của \(\frac{a}{b}\) và \(\frac{c}{d}\).

Lưu ý:

a) Muốn trừ một phân số cho một phân số ta quy đồng mẫu rồi lấy tử của phân số bị trừ trừ đi tử của phân số trừ và giữ nguyên mẫu chung.

b) Từ \(\frac{a}{b} +\frac{c}{d}=\frac{e}{f}\) ta suy ra \(\frac{a}{b} =\frac{e}{f}-\frac{c}{d}\) .

Thật vậy, ta có:

\(\frac{a}{b}=\frac{a}{b}+\left (\frac{c}{d}+\frac{-c}{d} \right )=\frac{a}{b}+\frac{c}{d}+\left (-\frac{c}{d} \right )\)

\(=\frac{e}{f}+\left (-\frac{c}{d} \right )=\frac{e}{f}-\frac{c}{d}\).

Tương tự, từ \(\frac{a}{b}-\frac{c}{d}=\frac{e}{f}\) hay \(\frac{a}{b}+\left (-\frac{c}{d} \right )=\frac{e}{f}\) suy ra

\(\frac{a}{b}+\left (-\frac{c}{d} \right )+\frac{c}{d}=\frac{e}{f}+\frac{c}{d}\) hay \(\frac{a}{b}=\frac{e}{f}+\frac{c}{d}.\)

Như vậy ta cũng có quy tắc chuyển vế như đối với số nguyên.

3. Ví dụ minh họa

Trước khi đi vào giải bài luyện tập bài §9: giải bài 63 64 65 66 trang 34 sgk toán 6 tập 2, chúng ta hãy tìm hiểu các ví dụ điển hình sau đây:

Ví dụ 1:

Tính \(\frac{2}{7} – \left( {\frac{{ – 1}}{4}} \right)\)

Bài giải:

\(\frac{2}{7} – \left( {\frac{{ – 1}}{4}} \right) = \frac{2}{7} + \frac{1}{4} = \frac{{8 + 7}}{{28}} = \frac{{15}}{{28}}\)

Nhận xét:

Ta có \(\left( {\frac{a}{b} – \frac{c}{d}} \right) + \frac{c}{d} = \left[ {\frac{a}{b} + \left( { – \frac{c}{d}} \right)} \right] + \frac{c}{d} = \frac{a}{b} + \left[ {\left( { – \frac{c}{d}} \right) + \frac{c}{d}} \right] = \frac{a}{b} + 0 = \frac{a}{b}\)

Vậy có thể nói hiệu \(\frac{a}{b} – \frac{c}{d}\) là một số mà cộng với \(\frac{c}{d}\) thì được \(\frac{a}{b}\)

Như vậy phép trừ (phân số) là phép toán ngược của phép cộng (phân số).

Ví dụ 2:

Thời gian 1 ngày của Cường được phân phối như sau:

Ngủ \(\frac{1}{3}\) ngày.

Học ở trường: \(\frac{1}{6}\) ngày.

Chơi thể thao: \(\frac{1}{{12}}\) ngày.

Học và làm tập ở nhà: \(\frac{1}{8}\) ngày.

Giúp đỡ gia đình việc vặt: \(\frac{1}{{24}}\) ngày.

Hỏi Cường còn bao nhiêu thời gian rỗi?

Bài giải:

Thời gian rỗi của Cường là \(\frac{1}{4}\) ngày.

Ví dụ 3:

a. Tính \(1 – \frac{1}{2},\,\,\,\,\,\,\,\frac{1}{2} – \frac{1}{3},\,\,\,\,\,\,\,\,\,\,\,\frac{1}{3} – \frac{1}{4},\,\,\,\,\,\,\,\,\,\,\frac{1}{4} – \frac{1}{5},\,\,\,\,\,\,\,\,\,\,\,\,\frac{1}{5} – \frac{1}{6}\)

b. Sử dụng kết quả của câu a) để tính nhanh tổng sau:

\(\frac{1}{2} + \frac{1}{6} + \frac{1}{{12}} + \frac{1}{{20}} + \frac{1}{{30}}\)

Bài giải:

a. \(\frac{1}{2},\,\,\frac{1}{6},\,\,\frac{1}{{12}},\,\frac{1}{{20}},\,\,\frac{1}{{30}}\)

b. \(\frac{1}{2} + \frac{1}{6} + \frac{1}{{12}} + \frac{1}{{20}} + \frac{1}{{30}} = \left( {1 – \frac{1}{2}} \right) + \left( {\frac{1}{2} – \frac{1}{3}} \right) + \left( {\frac{1}{3} – \frac{1}{4}} \right) + \left( {\frac{1}{4} – \frac{1}{5}} \right) + \left( {\frac{1}{5} – \frac{1}{6}} \right)\)

\( = 1 + \left( {\frac{{ – 1}}{2} + \frac{1}{2}} \right) + \left( {\frac{{ – 1}}{3} + \frac{1}{3}} \right) + \left( {\frac{{ – 1}}{4} + \frac{1}{4}} \right) + \left( {\frac{{ – 1}}{5} + \frac{1}{5}} \right) + \frac{{ – 1}}{6} = \frac{5}{6}\)

Ví dụ 4:

a. Chứng tỏ rằng với \(n \in \mathbb{N},n \ne 0\) thì:

\(\frac{1}{{n(n + 1)}} = \frac{1}{n} – \frac{1}{{n + 1}}\)

b. Áp dụng kết quả ở câu a) để tính:

\(A = \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + … + \frac{1}{{9.10}}\)

Bài giải:

a. \(\frac{1}{{n(n + 1)}} = \frac{{n + 1 – n}}{{n(n + 1)}} = \frac{{n + 1}}{{n(n + 1)}} – \frac{n}{{n(n + 1)}} = \frac{1}{n} – \frac{1}{{n + 1}}\)

b. \(S = 1 – \frac{1}{2} + \frac{1}{2} – \frac{1}{3} + \frac{1}{3} – \frac{1}{4} + … + \frac{1}{9} – \frac{1}{{10}} = 1 – \frac{1}{{10}} = \frac{9}{{10}}\)

Ví dụ 5:

Tính nhanh:

\(A = \frac{1}{6} + \frac{1}{{12}} + \frac{1}{{20}} + \frac{1}{{30}} + \frac{1}{{42}} + \frac{1}{{56}}\)

Bài giải:

\(A = \frac{1}{{2.3}} + \frac{1}{{3.4}} + \frac{1}{{4.5}} + \frac{1}{{5.6}} + \frac{1}{{6.7}} + \frac{1}{{7.8}}\)

\( = \frac{1}{2} – \frac{1}{3} + \frac{1}{3} – \frac{1}{4} + \frac{1}{4} – \frac{1}{5} + \frac{1}{5} – \frac{1}{6} + \frac{1}{6} – \frac{1}{7} + \frac{1}{7} – \frac{1}{8}\)

\( = \frac{1}{2} – \frac{1}{8} = \frac{3}{8}\)

Ví dụ 6:

Chứng tỏ rằng: \(D = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + …. + \frac{1}{{{{10}^2}}} < 1\)

Bài giải:

\(D = \frac{1}{{{2^2}}} + \frac{1}{{{3^2}}} + \frac{1}{{{4^2}}} + …. + \frac{1}{{{{10}^2}}} < \frac{1}{{1.2}} + \frac{1}{{2.3}} + \frac{1}{{3.4}} + … + \frac{1}{{9.10}}\)

\( = 1 – \frac{1}{2} + \frac{1}{2} – \frac{1}{3} + … + \frac{1}{9} – \frac{1}{{10}}\)

\( = 1 – \frac{1}{{10}} = \frac{9}{{10}} < 1\)

Dưới đây là giải bài luyện tập bài §9: giải bài 63 64 65 66 trang 34 sgk toán 6 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Luyện tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần số học 6 kèm bài giải chi tiết bài 63 64 65 66 trang 34 sgk toán 6 tập 2 của bài §9 Phép trừ phân số trong chương III – Phân số cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 63 64 65 66 trang 34 sgk toán 6 tập 2

1. Giải bài 63 trang 34 sgk Toán 6 tập 2

Điền phân số thích hợp vào ô vuông:

Bài giải:

a) Coi phân số phải tìm là x rồi vận dụng quy tắc chuyển vế để tìm x.

Ta có: \({\rm{c}}){1 \over 4} – x = {1 \over {20}}\). Chuyển vế ta được:

\(x = {1 \over 4} – {1 \over {20}} = {{5 – 1} \over {20}} = {4 \over {20}} = {1 \over 5}\)

b) Làm tương tự câu a ta có đáp số: \(11 \over 15 \);

c) Làm tương tự câu a ta có đáp số: \(1 \over 5 \);

d) Làm tương tự câu a ta có đáp số: \( – 8 \over 13 \).

2. Giải bài 64 trang 34 sgk Toán 6 tập 2

Hoàn thành các phép tính:

a) \({7 \over 9} – { \ldots \over 3} = {1 \over 9}\)

b) \({1 \over \ldots } – {{ – 2} \over {15}} = {7 \over {15}}\)

c) \({{ – 11} \over {14}} – {{ – 4} \over \ldots } = {{ – 3} \over {14}}\)

d) \({ \ldots \over {21}} – {2 \over 3} = {5 \over {21}}\)

Bài giải:

a) Thay dấu ba chấm bởi x rồi tìm x.

Ta có: \({7 \over 9} – {x \over 3} = {1 \over 9}\) . Từ đó suy ra: \({x \over 3} = {7 \over 9} – {1 \over 9}\) hay \({x \over 3} = {6 \over 9} = {2 \over 3}\)

Vậy x = 2

b) Làm tương tự câu a ta có đáp số: x = 3;

c) Làm tương tự câu a ta có đáp số: x = 7;

d) Làm tương tự câu a ta có đáp số: x =19.

3. Giải bài 65 trang 34 sgk Toán 6 tập 2

Buổi tối (từ 19 giờ đến 21 giờ 30 phút), Bình định dành \({1 \over 4}\) giờ để rửa bát, \({1 \over 6}\) giờ để quét nhà và 1 giờ để làm bài tập.Thời gian còn lại, Bình định dành để xem chương trình phim truyện truyền hình kéo dài 45 phút. Hỏi Bình định có đủ thời gian để xem hết phim không?

Bài giải:

Thời gian từ 19 giờ đến 21 giờ 30 phút là 2 giờ 30 phút hay \({5 \over 2}\) giờ.

Tổng thời gian rửa bát, quét nhà, làm bài tập là:

\({1 \over 4} + {1 \over 6} + 1 = {3 \over {12}} + {2 \over {12}} + {{12} \over {12}} = {{17} \over {12}}\) (giờ).

Do đó thời gian còn lại là: \({5 \over 2} – {{17} \over {12}} = {{30} \over {12}} – {{17} \over {12}} = {{13} \over {12}}\) (giờ)

Chương trình phim truyện kéo dài 45 phút hay \({{45} \over {60}}\) giờ hay \({9 \over {12}}\) giờ.

Vì \({9 \over {12}} < {{13} \over {12}}\) nên Bình có thừa thì giờ để xem phim này.

4. Giải bài 66 trang 34 sgk Toán 6 tập 2

Điền số thích hợp vào ô trống:

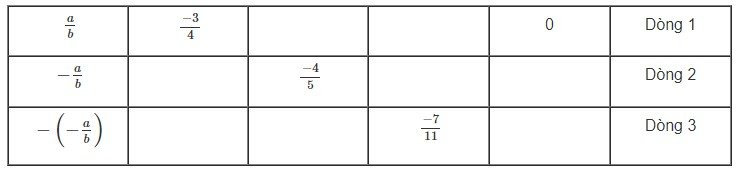
So sánh dòng 1 và dòng 3, em có thể nói gì về “số đối của số đối của một số” \( – \left( { – {a \over b}} \right)\) ?

Bài giải:

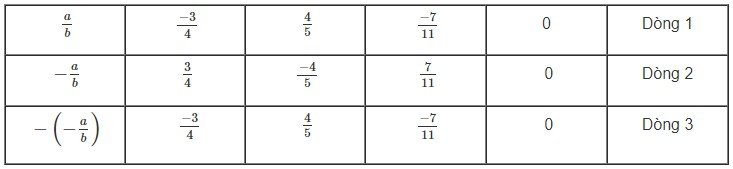
Câu trước:

Câu tiếp theo:

Luyện tập bài §9: Giải bài 67 68 trang 35 sgk toán 6 tập 2

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 6 với giải bài 63 64 65 66 trang 34 sgk toán 6 tập 2!

“Bài tập nào khó đã có giaibaisgk.com“