Nội Dung
Hướng dẫn giải Bài §11. Tính chất cơ bản của phép nhân phân số, chương III – Phân số, sách giáo khoa toán 6 tập hai. Nội dung bài giải bài 74 75 76 77 trang 39 sgk toán 6 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần số học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 6.
Lý thuyết
Bài học sẽ giúp các em tìm hiểu các vấn đề liên quan đến tính chất cơ bản của phép nhân phân số, tính chất chia hết cùng các dạng toán liên quan và các ví dụ minh họa có hướng dẫn giải sẽ giúp các em dễ dàng nắm được nội dung bài học.
1. Các tính chất
Tương tự phép nhân số nguyên, phép nhân phân số có các tính chất cơ bản sau:
a. Tính chất giao hoán: \(\frac{a}{b}.\frac{c}{d} = \frac{c}{d}.\frac{a}{b}\)
b. Tính chất kết hợp: \(\left( {\frac{a}{b}.\frac{c}{d}} \right).\frac{p}{q} = \frac{a}{b}.\left( {\frac{c}{d}.\frac{p}{q}} \right)\)
c. Nhân với số 1: \(\frac{a}{b}.1 = 1.\frac{a}{b} = \frac{a}{b}\)
d. Tính chất phân phối của phép nhân đối với phép cộng:
\(\frac{a}{b}.\left( {\frac{c}{d} + \frac{p}{q}} \right) = \frac{a}{b}.\frac{c}{d} + \frac{a}{b}.\frac{p}{q}\)
2. Áp dụng
Do các tính chất giao hoán và kết hợp của phép nhân, khi nhân nhiều phân số, ta có thể đổi chỗ hoặc nhóm các phân số lại theo bất cứ cách nào sao cho việc tính toán được thuận tiện.
Ví dụ: Tính tích \(M = \frac{{ – 7}}{{15}}.\frac{5}{8}.\frac{{15}}{{ – 7}}.( – 16)\)
Bài giải:
Ta có \(M = \frac{{ – 7}}{{15}}.\frac{{15}}{{ – 7}}.\frac{5}{8}.( – 16)\) (Tính chất giao hoán)
\( = \left( {\frac{{ – 7}}{{15}}.\frac{{15}}{{ – 7}}} \right).\left( {\frac{5}{8}.( – 16)} \right)\) (tính chất kết hợp)
\( = 1.( – 10) = – 10\) nhân với số 1
3. Ví dụ minh họa
Trước khi đi vào giải bài 74 75 76 77 trang 39 sgk toán 6 tập 2, chúng ta hãy tìm hiểu các ví dụ điển hình sau đây:
Ví dụ 1:
Tính nhanh giá trị các biểu thức
\(A = \frac{6}{7} + \frac{1}{7}.\frac{2}{7} + \frac{1}{7}.\frac{5}{7}\)
\(B = \frac{4}{9}.\frac{{13}}{3} – \frac{4}{3}.\frac{{40}}{9}\)
Bài giải:
\(A = \frac{1}{7}.\left( {6 + \frac{2}{7} + \frac{5}{7}} \right) = \frac{1}{7}.7 = 1\)
\(B = \frac{4}{9}.\left( {\frac{{13}}{3} – \frac{{40}}{3}} \right) = \frac{4}{9}.( – 9) = – 4\)
Ví dụ 2:
Áp dụng các tính chất của phép nhân phân số để tính nhanh.
\(M = \frac{8}{3}.\frac{2}{5}.\frac{3}{8}.10.\frac{{19}}{{92}}\)
\(N = \frac{5}{7}.\frac{5}{{11}} + \frac{5}{7}.\frac{2}{{11}} – \frac{5}{7}.\frac{{14}}{{11}}\)
\(Q = \left( {\frac{1}{{99}} + \frac{{12}}{{999}} – \frac{{123}}{{9999}}} \right).\left( {\frac{1}{2} – \frac{1}{3} – \frac{1}{6}} \right)\)
Bài giải:
\(M = \left( {\frac{8}{3}.\frac{3}{8}} \right).\left( {\frac{2}{5}.10} \right).\frac{{19}}{{92}} = 1.4.\frac{{19}}{{92}} = \frac{{19}}{{23}}\)
\(N = \frac{5}{7}.\left( {\frac{5}{{11}} + \frac{2}{{11}} – \frac{{14}}{{11}}} \right) = \frac{5}{7}.\frac{{ – 7}}{{11}} = \frac{{ – 5}}{{11}}\)
\(Q = \left( {\frac{1}{{99}} + \frac{{12}}{{999}} – \frac{{123}}{{9999}}} \right).0 = 0\)
Ví dụ 3:
Tính giá trị biểu thức:
\(A = \frac{{{1^2}}}{{1.2}}.\frac{{{2^2}}}{{2.3}}.\frac{{{3^2}}}{{3.4}}.\frac{{{4^2}}}{{4.5}}\)
\(B = \frac{{{2^2}}}{{1.3}}.\frac{{{3^2}}}{{2.4}}.\frac{{{4^2}}}{{3.5}}.\frac{{{5^2}}}{{4.6}}.\)
Bài giải:
\(A = \frac{1}{2}.\frac{2}{3}.\frac{3}{4}.\frac{4}{5} = \frac{1}{5}\)
\(B = \frac{{2\,\,.\,\,3\,\,.\,\,4\,\,.\,\,5}}{{1\,\,.\,\,2\,\,.\,\,3\,\,.\,\,4}}\,\,.\,\,\frac{{2\,\,.\,\,3\,\,.\,\,4\,\,.\,\,5}}{{3\,\,.\,\,4\,\,.\,\,5\,\,.\,\,6}} = \frac{5}{3}\)
Ví dụ 4:
Tính nhanh
\(M = \frac{2}{{3\,\,.\,\,5}} + \frac{2}{{5\,\,.\,\,7}} + \frac{2}{{7\,\,.\,\,9}} + … + \frac{2}{{97.99}}\)
Bài giải:
\(M = \left( {\frac{1}{3} – \frac{1}{5}} \right) + \left( {\frac{1}{5} – \frac{1}{7}} \right) + \left( {\frac{1}{7} – \frac{1}{9}} \right) + … + \left( {\frac{1}{{97}} – \frac{1}{{99}}} \right)\)
\( = \frac{1}{3} – \frac{1}{{99}}\)
\( = \frac{{32}}{{99}}\)
Ví dụ 5:
Tính giá trị của biểu thức:
\(M = \frac{1}{{1.2.3}} + \frac{1}{{2.3.4}} + \frac{1}{{3.4.5}} + …. + \frac{1}{{10.11.12}}\)
Bài giải:
Ta có nhận xét: \(\frac{1}{{1.2}} – \frac{1}{{2.3}} = \frac{{3 – 1}}{{1.2.3}} = \frac{2}{{1.2.3}}\)
\(\frac{1}{{2.3}} – \frac{1}{{3.4}} = \frac{{4 – 2}}{{2.3.4}} = \frac{2}{{2.3.4}};…\)
Suy ra \(\frac{1}{{1.2.3}} = \frac{1}{2}\left( {\frac{1}{{1.2}} – \frac{1}{{2.3}}} \right)\)
\(\frac{1}{{2.3.4}} = \frac{1}{2}\left( {\frac{1}{{2.3}} – \frac{1}{{3.4}}} \right);…\)
Do đó:
\(M = \frac{1}{2}\left( {\frac{1}{{1.2}} – \frac{1}{{2.3}} + \frac{1}{{2.3}} – \frac{1}{{3.4}} + …. + \frac{1}{{10.11}} – \frac{1}{{11.12}}} \right)\)
\( = \frac{1}{2}\left( {\frac{1}{{1.2}} – \frac{1}{{11.12}}} \right) = \frac{1}{2}\left( {\frac{1}{2} – \frac{1}{{11.12}}} \right)\)
\( = \frac{1}{2}.\frac{{65}}{{132}} = \frac{{65}}{{264}}\)
Dưới đây là Hướng dẫn giải bài 74 75 76 77 trang 39 sgk toán 6 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần số học 6 kèm bài giải chi tiết bài 74 75 76 77 trang 39 sgk toán 6 tập 2 của bài §11 Tính chất cơ bản của phép nhân phân số trong chương III – Phân số cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 74 trang 39 sgk Toán 6 tập 2
Điền các số thích hợp vào bảng sau:

Bài giải:

2. Giải bài 75 trang 39 sgk Toán 6 tập 2
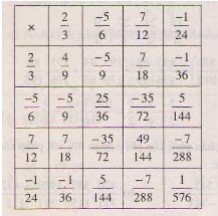
Hoàn thành bảng nhân sau (chú ý rút ngắn gọn nếu có thể):

Bài giải:
3. Giải bài 76 trang 39 sgk Toán 6 tập 2
Tính giá trị biểu thức sau một cách hợp lí:
\(A=\frac{7}{19}.\frac{8}{11}+\frac{7}{19}.\frac{3}{11}+\frac{12}{19}\) ;
\(B= \frac{5}{9}.\frac{7}{13}+\frac{5}{9}.\frac{9}{13}-\frac{5}{9}.\frac{3}{13}\) ;
\(C=\left (\frac{67}{111}+\frac{2}{33}-\frac{15}{117} \right ).\left (\frac{1}{3}-\frac{1}{4}-\frac{1}{12} \right )\).
Bài giải:
\(A= \frac{7}{19}.\left (\frac{8}{11}+\frac{3}{11} \right )+\frac{12}{19}=\frac{7}{19}.1 +\frac{12}{19}=1\).
\(B=\frac{5}{9}.\left (\frac{7}{13}+\frac{9}{13}-\frac{3}{13} \right )=\frac{5}{9}.\frac{7+9-3}{13}=\frac{5}{9}.\frac{13}{13}=\frac{5}{9}.\)
\(C=\left (\frac{67}{111}+\frac{2}{33}-\frac{15}{117} \right ).\left (\frac{1}{3}-\frac{1}{4}-\frac{1}{12} \right )\)
\(=\left (\frac{67}{111}+\frac{2}{33}-\frac{15}{117} \right ).\frac{4-3-1}{12}=\left (\frac{67}{111}+\frac{2}{33}-\frac{15}{117} \right ).0=0\)
4. Giải bài 77 trang 39 sgk Toán 6 tập 2
Tính giá trị các biểu thức sau:
\(A=a.\frac{1}{2} +a.\frac{1}{3}-a.\frac{1}{4}\) với \(a= \frac{-4}{5}\);
\(B=\frac{3}{4}.b+\frac{4}{3}.b-\frac{1}{2}.b\) với \(b=\frac{16}{9}\) ;
\(C=c.\frac{3}{4}+c.\frac{5}{6}-c.\frac{19}{12}\) với \(c=\frac{2002}{2003}\) ;
Bài giải:
Áp dụng tính chất phân phối, rồi tính giá trị biểu thức.
Chẳng hạn, \(A=a.\left (\frac{1}{2}+\frac{1}{3}-\frac{1}{4} \right )=a.\frac{6+4-3}{12}=a.\frac{7}{12}.\)
Với \(a= \frac{-4}{5}\) , thì \(A=\frac{-4}{5}.\frac{7}{12}=\frac{-7}{15}.\)
ĐS: \(B=\frac{1}{2}\) ; C = 0.
Bài trước:
Bài tiếp theo:
- Luyện tập bài §11: Giải bài 78 79 80 trang 40 sgk toán 6 tập 2
- Luyện tập bài §11: Giải bài 81 82 83 trang 41 sgk toán 6 tập 2
Xem thêm:
- Các bài toán 6 khác
- Để học tốt môn Vật lí lớp 6
- Để học tốt môn Sinh học lớp 6
- Để học tốt môn Ngữ văn lớp 6
- Để học tốt môn Lịch sử lớp 6
- Để học tốt môn Địa lí lớp 6
- Để học tốt môn Tiếng Anh lớp 6
- Để học tốt môn Tiếng Anh lớp 6 thí điểm
- Để học tốt môn Tin học lớp 6
- Để học tốt môn GDCD lớp 6
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 6 với giải bài 74 75 76 77 trang 39 sgk toán 6 tập 2!
“Bài tập nào khó đã có giaibaisgk.com“
