Hướng dẫn Giải bài 10 11 12 trang 76 sgk Toán 9 tập 1

Nội Dung

Hướng dẫn giải Bài §2. Tỉ số lượng giác của góc nhọn, chương I – Hệ thức lượng trong tam giác vuông, sách giáo khoa toán 9 tập một. Nội dung bài giải bài 10 11 12 trang 76 sgk toán 9 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 9.

Lý thuyết

1. Khái niệm tỉ số lượng giác của một góc nhọn

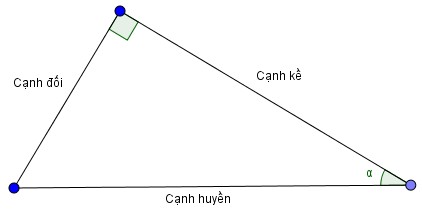
Nhận xét: Từ định nghĩa trên, dễ thấy các tỉ số lượng giác của một góc nhọn luôn luôn dương. Hơn nữa ta có: $sin\alpha < 1, cos\alpha <1$

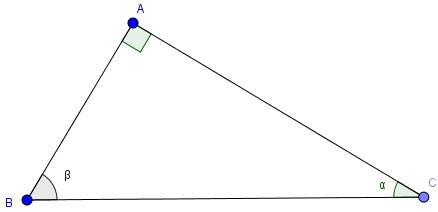
Chú ý: Nếu hai góc nhọn $\alpha$ và $\beta$ có $sin\alpha =sin\beta$ ( hoặc $cos\alpha =cos\beta , tan\alpha =tan\beta ,cotg \alpha =cotg\beta$ ) thì $\alpha =\beta$ vì chúng là hai góc tương ứng của hai tam giác vuông đồng dạng.

2. Tỉ số lượng giác của hai góc phụ nhau

ĐỊNH LÍ: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.

Cụ thể trong hình trên với $\alpha$ và $\beta$ là hai góc phụ nhau nên: $sin\alpha =cos\beta , cos\alpha =sin\beta, tan \alpha =cotg\beta , cotg\alpha =tan\beta$

Bảng tỉ số lượng giác của các góc đặc biệt:

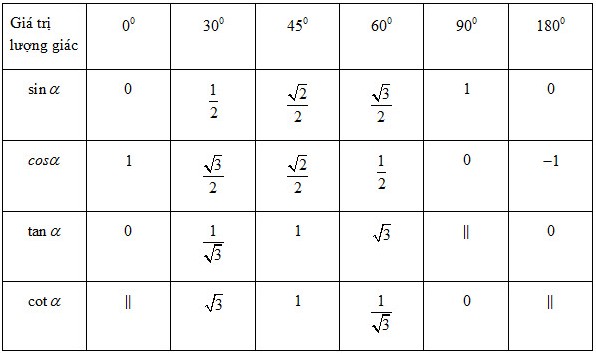
Chú ý: Từ nay khi viết các tỉ số lượng giác của một góc nhọn trong tam giác, ta bỏ kí hiệu “^”. Chẳng hạn viết $sinA$ thay vì viết $sin\widehat{A}$.

Từ định nghĩa các tỉ số lượng giác của một góc nhọn ta có: $tan\alpha =\frac{sin\alpha }{cos\alpha }; cotg\alpha =\frac{cos\alpha }{sin\alpha }$

và $tan\alpha .cotg\alpha =1 , sin^2\alpha +cos^2\alpha =1$; $1+tan^2\alpha =\frac{1}{cos^2\alpha }; 1+cot^2\alpha =\frac{1}{sin^2\alpha }$

Dưới đây là phần Hướng dẫn trả lời các câu hỏi có trong bài học cho các bạn tham khảo. Các bạn hãy đọc kỹ câu hỏi trước khi trả lời nhé!

Câu hỏi

1. Trả lời câu hỏi 1 trang 71 sgk Toán 9 tập 1

Xét tam giác $ABC$ vuông tại A có $\widehat A = \alpha $. Chứng minh rằng:

a) $\displaystyle \alpha = {45^o} \Leftrightarrow {{AC} \over {AB}} = 1$

b) $\displaystyle \alpha = {60^o} \Leftrightarrow {{AC} \over {AB}} = \sqrt 3 $

Trả lời:

a) Tam giác $ABC$ vuông tại A có $\widehat B = {45^0} \Rightarrow \Delta ABC$ vuông cân tại A $ \displaystyle \Rightarrow AB = AC \Rightarrow {{AB} \over {AC}} = 1$

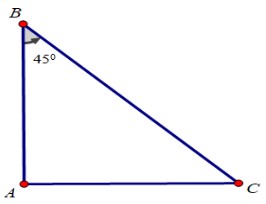
b) Kẻ trung tuyến $AD$ của tam giác vuông $ABC$

$ \displaystyle \Rightarrow AD = BD = {{BC} \over 2}$

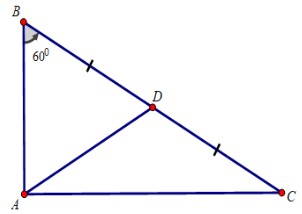
Tam giác $ABD$ có: $AD = BD,\,\,\widehat {ABD} = {60^o}$

$ \Rightarrow \Delta ABD$ là tam giác đều

$ \displaystyle \Rightarrow AB = AD = {{BC} \over 2} \Rightarrow BC = AB$

Áp dụng định lí Pytago vào tam giác ABC vuông tại A có:

$\eqalign{& A{B^2} + A{C^2} = B{C^2} \cr & \Leftrightarrow A{B^2} + A{C^2} = 4A{B^2} \cr & \Leftrightarrow A{C^2} = 3A{B^2} \Leftrightarrow AC = \sqrt 3 AB \cr & \Leftrightarrow {{AC} \over {AB}} = \sqrt 3 \cr} $

2. Trả lời câu hỏi 2 trang 73 sgk Toán 9 tập 1

Cho tam giác $ABC$ vuông tại $A$ có $\widehat C = \beta $. Hãy viết các tỉ số lượng giác của góc $\beta $

Trả lời:

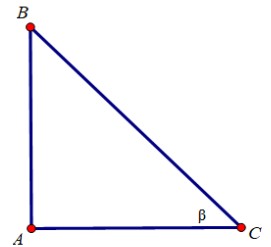
Các tỉ số lượng giác của góc $\beta $ là:

$\eqalign{& \sin \beta = {{AB} \over {BC}} \cr & \cos \beta = {{AC} \over {BC}} \cr & tg\beta = {{AB} \over {AC}} \cr & cotg\beta = {{AC} \over {AB}} \cr} $

3. Trả lời câu hỏi 3 trang 74 sgk Toán 9 tập 1

Hãy nêu cách dựng góc nhọn $\beta $ theo hình 18 và chứng minh cách dựng đó là đúng.

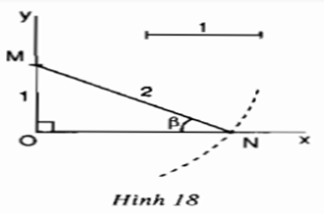
Trả lời:

♦ Cách dựng:

– Dựng góc $xOy$ bằng $90^0$

– Dựng đoạn OM trên trục Oy sao cho OM=1

– Dựng đường tròn tâm M bán kính bằng 2, đường tròn giao với tia Ox tại N

– Khi đó góc MNO là góc cần dựng

♦ Chứng minh:

Tam giác MON vuông tại O có: $MO=1; MN=2$

Khi đó: $\displaystyle \sin \beta = \sin \widehat {MNO} = {{MO} \over {MN}} = {1 \over 2} = 0,5$

4. Trả lời câu hỏi 4 trang 74 sgk Toán 9 tập 1

Cho hình 19. Hãy cho biết tổng số đo của góc $\alpha $ và góc $\beta $. Lập các tỉ số lượng giác của góc $\alpha $ và góc $\beta .$ Trong các tỉ số này, hãy cho biết các cặp tỉ số bằng nhau.

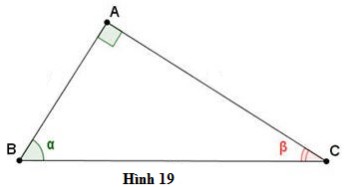
Trả lời:

Tam giác $ABC$ vuông tại $A$ nên $\widehat B + \widehat C = 90^\circ $ hay $\alpha + \beta = 90^\circ $

– Các tỉ số lượng giác của góc $\alpha $ là:

$\sin \alpha = \dfrac{{AC}}{{BC}};\cos \alpha = \dfrac{{AB}}{{BC}}$ $\tan \alpha = \dfrac{{AC}}{{AB}};\cot \alpha = \dfrac{{AB}}{{AC}}$

– Các tỉ số lượng giác của góc $\beta $ là:

$\cos \beta = \dfrac{{AC}}{{BC}};\sin \beta = \dfrac{{AB}}{{BC}}$ $\cot \beta = \dfrac{{AC}}{{AB}};\tan \beta = \dfrac{{AB}}{{AC}}$

Suy ra các cặp tỉ số bằng nhau là $\sin \alpha = \cos \beta ;\cos \alpha = \sin \beta ;\tan \alpha = \cot \beta ;\cot \alpha = \tan \beta $

Dưới đây là Hướng dẫn giải bài 10 11 12 trang 76 sgk toán 9 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 9 kèm bài giải chi tiết bài 10 11 12 trang 76 sgk toán 9 tập 1 của bài §2. Tỉ số lượng giác của góc nhọn trong chương I – Hệ thức lượng trong tam giác vuông cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 10 11 12 trang 76 sgk toán 9 tập 1

1. Giải bài 10 trang 76 sgk Toán 9 tập 1

Vẽ một tam giác vuông có một góc nhọn $34^0$ rồi viết các tỉ số lượng giác của góc $34^0$.

Bài giải:

Ta vẽ tam giác $ABC$ vuông tại B, có góc $A = 34^0$

Khi đó ta có các tỉ số lượng giác của góc $34^0$ là:

$sin 34^0 = sin A = \frac{BC}{AC}$.

$cos 34^0 = cos A = \frac{AB}{AC}$.

$tg 34^0 = tg A = \frac{BC}{AB}$.

$cotg 34^0 = cos A = \frac{AB}{BC}$.

2. Giải bài 11 trang 76 sgk Toán 9 tập 1

Cho tam giác $ABC$ vuông tại $C$, trong đó $AC = 0,9m, BC = 1,2m$. Tính các tỉ số lượng giác của góc $B$, từ đó suy ra các tỉ số lượng giác của góc $A$.

Bài giải:

Áp dụng định lí Pi-ta-go trong tam giác vuông $ABC$, ta có:

$AB^2 = AC^2 + BC^2$

$= (0,9)^2 + (1,2)^2 = 0,81 + 1,44 = 2,25$

$⇒ AB = \sqrt{2,25} = 1,5$

Tỉ số lượng giác của góc $B$:

$sin B = \frac{AC}{AB} = \frac{0,9}{1,5} = \frac{3}{5}$.

$cos B = \frac{BC}{AB} = \frac{1,2}{1,5} = \frac{4}{5}$.

$tg B = \frac{AC}{BC} = \frac{0,9}{1,2} = \frac{3}{4}$.

$cotg B = \frac{BC}{AC} = \frac{1,2}{0,9} = \frac{4}{3}$

Vì $ABC$ là tam giác vuông tại $C$ nên $\widehat{B}$ phụ với $\widehat{A}$. Do đó:

$sin A = cos B = \frac{4}{5}$.

$cos A = sin B = \frac{3}{5}$.

$tg A = cotg B = \frac{4}{3}$.

$cotg A = tg B = \frac{3}{4}$.

3. Giải bài 12 trang 76 sgk Toán 9 tập 1

Hãy viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn $45^0$:

sin $60^0$, cos $75^0$, sin $52^0$30′, cotg sin $82^0$, tg sin $80^0$

Bài giải:

Áp dụng định lí về tỉ số lượng giác của hai góc phụ nhau, ta có:

$sin 60^0 = cos 30^0$.

$cos 75^0 = sin 15^0$.

$sin 52^030′ = cos 37^030′.$

$cotg 82^0 = tg 8^0$.

$tg 80^0 = cotg 10^0$

Bài trước:

Luyện tập: Giải bài 5 6 7 8 9 trang 69 70 sgk Toán 9 tập 1

Bài tiếp theo:

Luyện tập: Giải bài 13 14 15 16 17 trang 77 sgk Toán 9 tập 1

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với giải bài 10 11 12 trang 76 sgk toán 9 tập 1!

“Bài tập nào khó đã có giaibaisgk.com“