Nội Dung
Hướng dẫn giải Bài §4. Liên hệ giữa phép chia và phép khai phương, chương I – Căn bậc hai. Căn bậc ba, sách giáo khoa toán 9 tập một. Nội dung bài giải bài 28 29 30 31 trang 18 19 sgk toán 9 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần đại số có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 9.
Lý thuyết
1. Định lí
Với số a không âm và số b dương, ta có: \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\)
2. Áp dụng
a) Quy tắc khai phương một thương
Muốn khai phương một thương \(\frac{a}{b}\), trong đó số a không âm và số b dương, ta có thể lần lượt khai phương số a và số b, rồi lấy kết quả thứ nhất chia cho kết quả thứ hai.
b) Quy tắc chia hai căn bậc hai
Muốn chia hai căn bậc hai của số a không âm cho căn bậc hai của số b dương, ta có có thể chia số a cho số b rồi khai phương kết quả đó.
Dưới đây là phần Hướng dẫn trả lời các câu hỏi có trong bài học cho các bạn tham khảo. Các bạn hãy đọc kỹ câu hỏi trước khi trả lời nhé!
Câu hỏi
1. Trả lời câu hỏi 1 trang 16 sgk Toán 9 tập 1
Tính và so sánh: \(\displaystyle \sqrt {{{16} \over {25}}} \) và \(\displaystyle {{\sqrt {16} } \over {\sqrt {25} }}\)
Trả lời:
Ta có:
+) \(\displaystyle \sqrt {{{16} \over {25}}} = \sqrt {{{\left( {{4 \over 5}} \right)}^2}} = {4 \over 5}\)
+) \(\displaystyle {{\sqrt {16} } \over {\sqrt {25} }} = {4 \over 5}\)
\( \displaystyle \Rightarrow \sqrt {{{16} \over {25}}} = {{\sqrt {16} } \over {\sqrt {25} }}\)
2. Trả lời câu hỏi 2 trang 17 sgk Toán 9 tập 1
Tính.
a) \(\displaystyle \sqrt {{{226} \over {256}}} \); b) \(\sqrt {0,0196} \)
Trả lời:
a) \(\displaystyle \sqrt {{{226} \over {256}}} = {{\sqrt {226} } \over {\sqrt {256} }} = {{15} \over {16}}\)
b) \(\displaystyle \sqrt {0,0196} = \sqrt {{{196} \over {10000}}} \)
\(\displaystyle = {{\sqrt {196} } \over {\sqrt {10000} }} = {{14} \over {100}} = 0,14\)
3. Trả lời câu hỏi 3 trang 18 sgk Toán 9 tập 1
Tính: a) \(\displaystyle {{\sqrt {999} } \over {\sqrt {111} }}\); b) \(\displaystyle {{\sqrt {52} } \over {\sqrt {117} }}\)
Trả lời:
Ta có:
a) \(\displaystyle {{\sqrt {999} } \over {\sqrt {111} }} = \sqrt {{{999} \over {111}}} = \sqrt 9 = 3\)
b) \(\displaystyle {{\sqrt {52} } \over {\sqrt {117} }} \)\(\displaystyle = \sqrt {{{52} \over {117}}} = \sqrt {{4 \over 9}} = \dfrac{2}{3}\)
4. Trả lời câu hỏi 4 trang 18 sgk Toán 9 tập 1
Rút gọn:
a) \(\sqrt {\dfrac{{2{a^2}{b^4}}}{{50}}} \)
b) \(\dfrac{{\sqrt {2a{b^2}} }}{{\sqrt {162} }}\) với \(a \ge 0.\)
Trả lời:
a) Ta có:
$\sqrt {\dfrac{{2{a^2}{b^4}}}{{50}}} = \sqrt {\dfrac{{{a^2}{b^4}}}{{25}}}$
$ = \dfrac{{\sqrt {{a^2}{b^4}} }}{{\sqrt {25} }} = \dfrac{{\sqrt {{a^2}} .\sqrt {{b^4}} }}{5}$
$ = \dfrac{{|a|{b^2}}}{5}$
b) Ta có:
$\dfrac{{\sqrt {2a{b^2}} }}{{\sqrt {162} }} = \sqrt {\dfrac{{2a{b^2}}}{{162}}} $
$= \sqrt {\dfrac{{a{b^2}}}{{81}}} = \dfrac{{\sqrt {a{b^2}} }}{{\sqrt {81} }} $
$= \dfrac{{\sqrt a .\sqrt {{b^2}} }}{9} = \dfrac{{\left| b \right|\sqrt a }}{9}$
Dưới đây là Hướng dẫn giải bài 28 29 30 31 trang 18 19 sgk toán 9 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần đại số 9 kèm bài giải chi tiết bài 28 29 30 31 trang 18 19 sgk toán 9 tập 1 của bài §4. Liên hệ giữa phép chia và phép khai phương trong chương I – Căn bậc hai. Căn bậc ba cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
1. Giải bài 28 trang 18 sgk Toán 9 tập 1
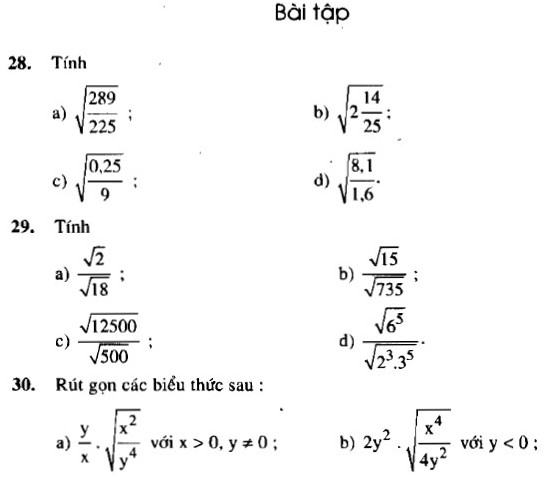
Tính:
a) $\sqrt{\frac{289}{225}}$; b) $\sqrt{2\frac{14}{25}}$
c) $\sqrt{\frac{0,25}{9}}$; d) $\sqrt{\frac{8,1}{1,6}}$
Bài giải:
a) Ta có:
$\sqrt{\frac{289}{225}}$ = $\frac{\sqrt{289}}{\sqrt{225}}$ = $\frac{17}{15}$
b) Ta có:
$\sqrt{2\frac{14}{25}}$ = $\frac{\sqrt{64}}{\sqrt{25}}$ = $\frac{8}{5}$
c) Ta có:
$\sqrt{\frac{0,25}{9}}$ = $\frac{\sqrt{0,25}}{\sqrt{9}}$ = $\frac{0,5}{3}$ = $\frac{1}{6}$
d) Ta có:
$\sqrt{\frac{8,1}{1,6}}$ = $\frac{\sqrt{81}}{\sqrt{16}}$ = $\frac{9}{4}$
2. Giải bài 29 trang 19 sgk Toán 9 tập 1
Tính:
a) $\frac{\sqrt{2}}{\sqrt{18}}$ ; b) $\frac{\sqrt{15}}{\sqrt{735}}$
c) $\frac{\sqrt{12500}}{\sqrt{500}}$ ; d) $\frac{\sqrt{6^5}}{\sqrt{2^3 . 3^5}}$
Bài giải:
a) Ta có:
$\frac{\sqrt{2}}{\sqrt{18}}$ = $\sqrt{\frac{2}{18}}$
= $\sqrt{\frac{1}{9}}$ = $\frac{1}{3}$
b) Ta có:
$\frac{\sqrt{15}}{\sqrt{735}}$ = $\sqrt{\frac{15}{735}}$
= $\sqrt{\frac{1}{49}}$ = $\frac{1}{7}$
c) Ta có:
$\frac{\sqrt{12500}}{\sqrt{500}}$ = $\sqrt{\frac{12500}{500}}$
= $\sqrt{\frac{25}{1}} = 5$
d) Ta có:
$\dfrac{\sqrt{6^{5}}}{\sqrt{2^{3}.3^{5}}}=\sqrt{\dfrac{6^5}{2^3.3^5}}$
$=\sqrt{\dfrac{(2.3)^5}{2^3.3^5}}=\sqrt{\dfrac{2^5.3^5}{2^3.3^5}}$
$=\sqrt{\dfrac{2^5.3^5}{2^3.3^5}}=\sqrt{\dfrac{2^5}{2^3}}$
$=\sqrt{\dfrac{2^3.2^2}{2^3}}=\sqrt{2^2}=2$
3. Giải bài 30 trang 19 sgk Toán 9 tập 1
Rút gọn các biểu thức sau:
a) $\frac{x}{y}$ . $\sqrt{\frac{x^2}{y^4}}$ với $x > 0, y \neq 0$
b) 2$y^2$ . $\sqrt{\frac{x^4}{4y^2}}$ với $y < 0$
c) 5xy . $\sqrt{\frac{25x^2}{y^6}}$ với $x < 0, y > 0$
d) 0,2$x^3$$y^3$ . $\sqrt{\frac{16}{x^4y^8}}$ với x $\neq$ 0, y $\neq$ 0
Bài giải:
a) Ta có:
\(\dfrac{y}{x}.\sqrt{\dfrac{x^{2}}{y^{4}}}=\dfrac{y}{x}.\dfrac{\sqrt{x^2}}{\sqrt{y^{4}}}\)
\(=\dfrac{y}{x}.\dfrac{\sqrt{x^2}}{\sqrt{(y^2)^2}}=\dfrac{y}{x}.\dfrac{|x|}{|y^2|}\)
Vì \(x> 0\) nên \(|x|=x\).
Vì \(y \ne 0\) nên \(y^2 > 0 \Rightarrow |y^2|=y^2\).
\(\Rightarrow \dfrac{y}{x}.\dfrac{|x|}{|y^2|} =\dfrac{y}{x}.\dfrac{x}{y^2}=\dfrac{y}{x}.\dfrac{x}{y.y}=\dfrac{1}{y}\).
Vậy \(\dfrac{y}{x}.\sqrt{\dfrac{x^{2}}{y^{4}}}=\dfrac{1}{y}\).
b) Ta có:
\(2y^2.\sqrt{\dfrac{x^{4}}{4y^{2}}}=2y^2.\dfrac{\sqrt{x^4}}{\sqrt{4y^2}}=2y^2.\dfrac{\sqrt{(x^2)^2}}{\sqrt{2^2.y^2}}\)
\(=2y^2.\dfrac{\sqrt{(x^2)^2}}{\sqrt{(2y)^2}}=2y^2.\dfrac{|x^2|}{|2y|}\)
Vì \(x^2 \ge 0 \Rightarrow |x^2|=x^2\).
Vì \(y<0\) nên \(2y < 0 \Rightarrow |2y|=-2y\)
\(\Rightarrow 2y^2.\dfrac{|x^2|}{|2y|}=2y^2.\dfrac{x^2}{-2y}=\dfrac{2y^2.x^2}{-2y}\)
\(=\dfrac{x^2.y.2y}{-2y}=-x^2y\).
Vậy \(2y^2.\sqrt{\dfrac{x^{4}}{4y^{2}}}=-x^2y\).
c) Ta có:
$ 5xy.\sqrt{\dfrac{25x^{2}}{y^{6}}}=5xy.\dfrac{\sqrt{25x^2}}{\sqrt{y^6}}$
$ =\dfrac{\sqrt{5^2.x^2}}{\sqrt{(y^3)^2}}=\dfrac{\sqrt{(5x)^2}}{\sqrt{(y^3)^2}}$
$ =5xy.\dfrac{|5x|}{|y^3|}$
Vì \(x<0 \Rightarrow |5x|=-5x\).
Vì \(y>0 \Rightarrow y^3 >0 \Rightarrow |y^3|=y^3\).
\( \Rightarrow 5xy.\dfrac{|5x|}{|y^3|}=5xy.\dfrac{-5x}{y^3}=\dfrac{5xy.(-5x)}{y^3}\)
\(=\dfrac{[5.(-5)].(x.x).y}{y^2.y}=\dfrac{-25x^2}{y^2}\)
Vậy \(5xy.\sqrt{\dfrac{25x^{2}}{y^{6}}}=\dfrac{-25x^2}{y^2}\).
d) Ta có:
\(0,2x^{3}y^{3}.\sqrt{\dfrac{16}{x^{4}y^{8}}}=0,2x^3y^3.\dfrac{\sqrt{16}}{\sqrt{x^4y^8}}\)
\(=0,2x^3y^3\dfrac{\sqrt{4^2}}{\sqrt{(x^2)^2.(y^4)^2}}\)
$=0,2x^3y^3.\dfrac{\sqrt{4^2}}{\sqrt{(x^2)^2}.\sqrt{(y^4)^2}}$
$ =0,2x^3y^3.\dfrac{4}{|x^2|.|y^4|}$ .
Vì \(x \ne 0,\ y \ne 0\) nên \( x^2 \ge 0\) và \(y^4 \ge 0\)
\(\Rightarrow |x^2| =x^2\) và \(|y^4|=y^4\).
\( \Rightarrow 0,2x^3y^3.\dfrac{4}{|x^2|.|y^4|}=0,2x^3y^3.\dfrac{4}{x^2y^4}\)
\(=\dfrac{0,2x^3y^3.4}{x^2y^4}\)
\(=\dfrac{(0,2.4).(x^2.x).y^3}{x^2.(y^3.y)}=\dfrac{0,8.x.x^2y^3}{y.x^2y^3}=\dfrac{0,8x}{y}\).
Vậy \(0,2x^{3}y^{3}.\sqrt{\dfrac{16}{x^{4}y^{8}}}=\dfrac{0,8x}{y}\).
4. Giải bài 31 trang 19 sgk Toán 9 tập 1
a) So sánh: $\sqrt{25 – 16}$ và $\sqrt{25}$ – $\sqrt{16}$
b) Chứng minh rằng: với a > b > 0 thì $\sqrt{a}$ – $\sqrt{b}$ < $\sqrt{a – b}$
Bài giải:
a) Ta có:
+) \( \sqrt {25 – 16} = \sqrt 9 =\sqrt{3^2}= 3.\)
+) \( \sqrt {25} – \sqrt {16} = \sqrt{5^2}-\sqrt{4^2}=5 – 4 = 1 \).
Vì \(3>1 \Leftrightarrow \sqrt {25 – 16}>\sqrt {25} – \sqrt {16} \).
Vậy \(\sqrt {25 – 16} > \sqrt {25} – \sqrt {16} \)
b) Theo bài \(26\), ta đã chứng minh được: Với \(a>0\) và \(b>0\) thì:
\( \sqrt{a+b}<\sqrt{a}+\sqrt{b}\).
Theo giải thiết, ta có
+) \(b>0 \)
+) \(a>b \Rightarrow a-b >0\)
Áp dụng bài \(26\) cho hai số \(a-b\) và \(b \), ta được:
\(\sqrt{(a-b) +b}< \sqrt{a-b}+\sqrt{b}\)
\(\Leftrightarrow \sqrt{a-b+b} < \sqrt{a-b} +\sqrt{b}\)
\(\Leftrightarrow \sqrt a < \sqrt{a-b}+\sqrt b\)
\(\Leftrightarrow \sqrt a – \sqrt b < \sqrt{a-b}\) (đpcm).
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 9 khác
- Để học tốt môn Vật lí lớp 9
- Để học tốt môn Sinh học lớp 9
- Để học tốt môn Ngữ văn lớp 9
- Để học tốt môn Lịch sử lớp 9
- Để học tốt môn Địa lí lớp 9
- Để học tốt môn Tiếng Anh lớp 9
- Để học tốt môn Tiếng Anh lớp 9 thí điểm
- Để học tốt môn Tin học lớp 9
- Để học tốt môn GDCD lớp 9
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với giải bài 28 29 30 31 trang 18 19 sgk toán 9 tập 1!
“Bài tập nào khó đã có giaibaisgk.com“
