Nội Dung
Bài ôn tập chương III – Quan hệ giữa các yếu tố trong tam giác – Các đường đồng quy của tam giác, sách giáo khoa toán 7 tập hai. Nội dung bài giải bài 63 64 65 66 67 68 69 70 trang 87 88 sgk toán 7 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 7.
Lý thuyết
Bảng tổng kết các kiến thức cần nhớ
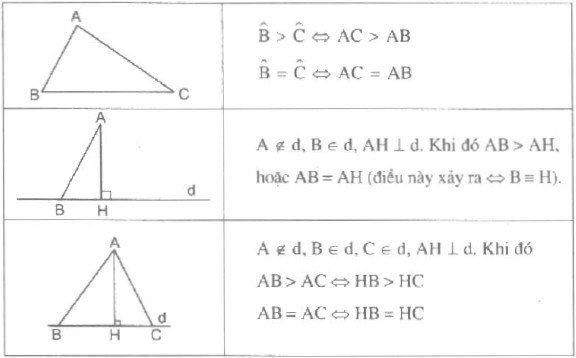

Dưới đây là Hướng dẫn giải bài 63 64 65 66 67 68 69 70 trang 87 88 sgk toán 7 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 7 kèm bài giải chi tiết bài 63 64 65 66 67 68 69 70 trang 87 88 sgk toán 7 tập 2 của Bài ôn tập chương III – Quan hệ giữa các yếu tố trong tam giác – Các đường đồng quy của tam giác, sách giáo khoa toán 7 tập hai cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 63 trang 87 sgk Toán 7 tập 2
Cho tam giác ABC với AC < AB. Trên tia đối của tia BC lấy điểm D sao cho BD = AB. Trên tia đối của tia CB lấy điểm E sao cho CE = AC. Vẽ các đonạ thẳng AD, AE.
a) Hãy so sánh góc ADC và góc AEB.
b) Hãy so sánh các đoạn thẳng AD và AE.
Bài giải:
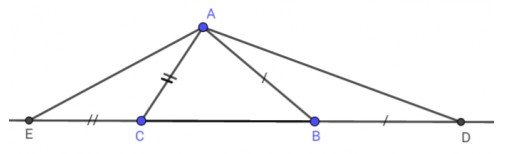
a) Xét tam giác ABC có: $AC<AB(gt)$
$\Rightarrow \widehat{ABC}<\widehat{ACB}\,\ (1)$ (quan hệ giữa cạnh và góc đối diện trong tam giác)
Vì $AB = BD(gt)\Rightarrow \Delta ABD$ cân tại $B$
$\Rightarrow \widehat{ADB}=\widehat{DAB}$
Mà $\widehat{ABC}=\widehat{ADB}+\widehat{DAB}$ (góc ngoài tam giác ABD)
$\Rightarrow \widehat{ADB}=\widehat{DAB}=\frac{1}{2}.\widehat{ABC}\,\ (2)$
Chứng minh tương tự với tam giác $AEC$
$\Rightarrow \widehat{AEC}=\frac{1}{2}.\widehat{ACB}\,\ (3)$
Từ (1)(2)(3) $\Rightarrow \widehat{ADC}<\widehat{AEB}$ (đpcm)
b) Xét tam giác $ADE$ có: $\widehat{ADE}<\widehat{AED}\,\ (cmt)$
$\Rightarrow AE < AD$ (quan hệ giữa cạnh và góc đối diện trong tam giác)
2. Giải bài 64 trang 87 sgk Toán 7 tập 2
Gọi MH là đường cao của tam giác MNP. Chứng minh rằng: Nếu MN < MP thì HN < HP và $\widehat{NMH}<\widehat{PMH}$ (yêu cầu xét hai trường hợp: khi góc N nhọn và khi góc N tù).
Bài giải:

♦ Trường hợp góc N nhọn
$\Delta MNP$ có $\widehat{N}$ nhọn nên chân đường cao $H$ từ $M$ nằm giữa $N$ và $P$.
Ta có: hình chiếu tương ứng của $MN,MP$ lần lượt là $NH,HP$.
Từ đề bài: $MN<MP\Rightarrow HN<HP$ (quan hệ giữa đường xiên và hình chiếu)
Xét $\Delta MNP$ có: $MN<MP$
$\Rightarrow \widehat{MPN}<\widehat{MNP}$ (quan hệ giữa cạnh và góc đối diện trong tam giác)
Vì $\widehat{NMH}+\widehat{MNH}=90^0$ (do tam giác MNH vuông tại H)
và $\widehat{PMH}+\widehat{MPH}=90^0$ (do tam giác MHP vuông tại H)
$\Rightarrow \widehat{NMH}<\widehat{PMH}$ (đpcm)
♦ Trường hợp góc N tù
$\Delta MNP$ có $\widehat{N}$ tù nên chân đường cao $H$ từ $M$ nằm ngoài $N$ và $P$. Tức là $N$ nằm giữa $H$ và $P$.
$\Rightarrow HN<HP$ (đpcm)
Vì $N$ nằm giữa $H$ và $P$ nên tia $MN$ ở giữa hai tia $MH$ và $MP$.
Suy ra $\widehat{NMH}<\widehat{PMH}$ (đpcm)
3. Giải bài 65 trang 87 sgk Toán 7 tập 2
Có thể vẽ được mấy tam giác (phân biệt) với ba cạnh là ba trong năm đoạn thẳng có độ dài như sau: 1cm, 2cm, 3cm, 4cm và 5cm?
Bài giải:
Để tạo được một tam giác thì độ dài ba cạnh phải thoả mãn bất đẳng thức tam giác. Đó là tổng độ dài hai cạnh bất kỳ phải lớn hơn cạnh còn lại.
Vì vậy chỉ có bộ ba độ dài sau thoả mãn (2,3,4); (2,4,5); (3,4,5).

4. Giải bài 66 trang 87 sgk Toán 7 tập 2
Đố: Bốn điểm dân cư được xây dựng như hình 58. Hãy tìm vị trí đặt một nhà máy sao cho tổng khoảng cách từ nhà máy đến bốn điểm dân cư này là nhỏ nhất.
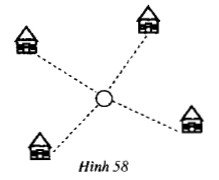
Bài giải:
Gọi O là một điểm tùy ý (nơi phải đặt nhà máy). A, B, C, D lần lượt là bốn điểm dân cư.
Tổng khoảng cách từ nhà máy đến 4 khu dân cư là: $OA + OB + OC + OD$.

Ta có:
Nếu O nằm trên đoạn AC thì:
$OA + OC = AC$
$OB + OD > BD$ (bất đẳng thức tam giác trong tam giác OBD)
$\Rightarrow OA + OB + OC + OD > AC + BD$
Nếu O nằm trên đoạn BD thì:
$OB + OD = BD$
$OA + OC > AC$ (bất đẳng thức tam giác trong tam giác OAC)
$\Rightarrow OA + OB + OC + OD > AC + BD$
Nếu O không nằm trên AC và BD thì:
$OA + OC > AC$ (bất đẳng thức tam giác trong tam giác OAC)
$OB + OD > BD$ (bất đẳng thức tam giác trong tam giác OBD)
$\Rightarrow OA + OB + OC + OD > AC + BD$
Nếu O là giao điểm của AC và BD thì:
$OA + OB + OC + OD = AC + BD$
Vậy khi O là giao điểm của AC và BD thì tổng khoảng cách từ nhà máy này đến các khu dân cư là ngắn nhất.
5. Giải bài 67 trang 87 sgk Toán 7 tập 2
Cho tam giác MNP với trung tuyến MR và trọng tâm Q.
a) Tính tỉ số các diện tích của hai tam giác MNP và RPQ.
b) Tính tỉ số các diện tích của hai tam giác MNQ và RNQ.
c) So sánh các diện tích của hai tam giác RPQ và RNQ.
Từ kết quả trên, hãy chứng minh các tam giác QMN, QNP, QPM có cùng diện tích.
Gợi ý: Hai tam giác ở mỗi câu a, b, c có chung đường cao.
Bài giải:
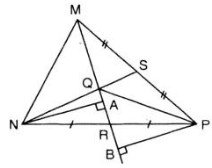
a) Vẽ $PB ⊥ MR$
Vậy tam giác $MPQ$ và $RPQ$ có chung đường cao $PB$
Vì $Q$ là trọng tâm của $ΔMNR$ nên $MQ = 2QR$ (suy ra từ tính chất trọng tâm của tam giác)
Ta có: $S_{\Delta MPQ}=\frac{1}{2}.MQ.PB=\frac{1}{2}.2QR.PB=QR.PB$
và $S_{\Delta PRQ}=\frac{1}{2}.QR.PB$
Suy ra $\frac{S_{\Delta MPQ}}{S_{\Delta PRQ}}=\frac{QR.PB}{\frac{1}{2}.QR.PB}=2$
b) Vẽ $NA ⊥ MR$
Vậy $NA$ là đường cao của $ΔMNQ$ đồng thời là đường cao của $ΔRNQ$.
Vì $Q$ là trọng tâm của $ΔMNP$ nên $MQ = 2QR$.
Ta có: $S_{\Delta MNQ}=\frac{1}{2}.MQ.NA=\frac{1}{2}.2QR.NA=QR.NA$
và $S_{\Delta NRQ}=\frac{1}{2}.QR.NA$
Suy ra $\frac{S_{\Delta MNQ}}{S_{\Delta NRQ}}=\frac{QR.NA}{\frac{1}{2}.QR.NA}=2$
c) Xét hai tam giác vuông $NAR$ và $PBR$, ta có:
$NR=PR (gt)$
$\widehat{NRA}=\widehat{PRB}$ (đối đỉnh)
$\Rightarrow \Delta NAR = \Delta PBR$ (cạnh huyền – góc nhọn)
$\Rightarrow NA =PB$ (cạnh tương ứng)
Ta có: $S_{\Delta PRQ}=\frac{1}{2}.QR.PB=\frac{1}{2}.QR.NA=S_{\Delta NRQ}$
Vậy: $S_{\Delta PRQ}=S_{\Delta NRQ}$ (đpcm)
Từ kết quả câu a) ta có:
$S_{ΔQPM} = 2.S_{ΔPRQ} = S_{ΔQNP}$ (do câu c) (*)
Từ kết quả câu b) ta có:
$S_{ΔQMN} = 2S_{ΔRNQ }= S_{ΔQNP}$ (**)
Từ (*) và (**) suy ra:
$S_{ΔQMN} = S_{ΔQNP} = S_{ΔQPM}$ (đpcm)
6. Giải bài 68 trang 88 sgk Toán 7 tập 2
Cho góc xOy. Hai điểm A, B lần lượt nằm trên hai cạnh Ox, Oy.
a) Hãy tìm điểm M cách đều hai cạnh góc xOy và cách đều hai điểm A, B.
b) Nếu OA = OB thì có bao nhiêu điểm M thỏa mãn các điều kiện trong câu a?
Bài giải:

a) Tìm $M$ khi độ dài $OA, OB$ là bất kì.
Vì $M$ cách đều hai cạnh $Ox, Oy$ của góc $xOy$ nên $M$ nằm trên đường phân giác $Oz$ của góc $xOy (1)$.
Vì $M$ cách đều hai điểm $A, B$ nên $M$ nằm trên đường trung trực của đoạn $AB (2)$.
Từ (1) và (2) ta xác định được điểm $M$ là giao điểm của đường phân giác $Oz$ của góc $xOy$ và đường trung trực của đoạn $AB$.
b) Tìm $M$ khi $OA = OB$
Vì điểm $M$ cách đều hai cạnh của góc $xOy$ nên $M$ nằm trên đường phân giác của góc $xOy (3)$.
Ta có $OA = OB$. Vậy $ΔAOB$ cân tại O.
Trong tam giác cân $OAB$ đường phân giác $Oz$ cũng là đường trung trực của đoạn $AB (4)$.
Từ (3) và (4) ta xác định được vô số điểm $M$ nằm trên đường phân giác $Oz$ của góc $xOy$ thỏa mãn điều kiện bài toán.
7. Giải bài 69 trang 88 sgk Toán 7 tập 2
Cho hai đường thẳng phân biệt không song song a và b, điểm M nằm bên trong hai đường thẳng này. Qua M lần lượt vẽ đường thẳng c vuông góc với a tại P, cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S. Chứng minh rằng đường thẳng qua M, vuông góc với SQ cũng đi qua giao điểm của a và b.
Bài giải:

Vì $a $và $b$ không song song nên chúng cắt nhau giả sử tại $A$.
Xét $ΔAQS$ có:
$QP ⊥ AS$ (vì $QP ⊥ a$)
$SR ⊥ AQ$ (vì $SR ⊥ b$)
Ta có $QP$ và $RS $ cắt nhau tại $M$. Vậy $M$ là trực tâm của $ΔAQS$.
$\Rightarrow $ Đường thẳng đi qua $M$ và vuông góc với $QS$ tại $H$ sẽ là đường cao thứ ba của $ΔAQS$.
Vậy $MH$ phải đi qua đỉnh $A $của Δ$AQS$ hay đường thẳng vuông góc với $QS$ đi qua giao điểm của $a$ và $b$ (đpcm).
8. Giải bài 70 trang 88 sgk Toán 7 tập 2
Cho A, B là hai điểm phân biệt và d là đường trung trực của đoạn thẳng AB.
a) Ta kí hiệu $P_A$ là nửa mặt phẳng bờ d có chưa điểm A (không kể đường thẳng d). Gọi là một điểm của $P_A$ và M là giao điểm của đường thẳng NB và d. Hãy so sánh NB với NM + MA; từ đó suy ra NA < NB.
b) Ta kí hiệu $P_B$ là nửa mặt phẳng bờ d có chứa điểm B (không kể d). Gọi N’ là một điểm của $P_B$. Chứng minh N’B < N’A.
c) Gọi L là một điểm sao cho LA < LB. Hỏi điểm L nằm ở đâu, trong $P_A, P_B$ hay trên d?
Bài giải:

a) Ta có $M$ nằm trên đường trung trực của $AB$ nên $MA = MB$.
Vì $M$ nằm trên đoạn $NB$ nên:
$NB = NM + MB$ hay $NB = NM + MA$ (vì $MB = MA$)
Vậy $NB = NM + MA$
Trong $ΔNMA$ có: $NA < NM + MA$
Vì $NM + MA = NB$ nên $NA < NB$ (đpcm)
b) Nối $N’A$ cắt $d$ tại $P$. Vì $P$ nằm trên đường trung trực của đoạn $AB$ nên: $PA = PB$
Ta có: $N’A = N’P + PA = N’P + PB$
Trong $ΔN’PB$ ta có: $N’B < N’P + PB$
Do đó: $N’B < N’A $(đpcm)
c) Vì $LA < LB$ nên $L$ không thuộc đường trung trực $d$.
Từ câu b) ta suy ra với điểm $N’$bất kì thuộc $P_B$ thì ta có $N’B < N’A$. Do đó, để $LA < LB$ thì $L$ không thuộc $P_B$.
Từ câu a) ta suy ra với điểm $N$ bất kì thuộc $P_A$ thì ta có $NA < NB$. Do đó, để $LA < LB$ thì $L$thuộc $P_A$.
Bài trước:
Xem thêm:
- Các bài toán 7 khác
- Để học tốt môn Vật lí lớp 7
- Để học tốt môn Sinh học lớp 7
- Để học tốt môn Ngữ văn lớp 7
- Để học tốt môn Lịch sử lớp 7
- Để học tốt môn Địa lí lớp 7
- Để học tốt môn Tiếng Anh lớp 7
- Để học tốt môn Tiếng Anh lớp 7 thí điểm
- Để học tốt môn Tin học lớp 7
- Để học tốt môn GDCD lớp 7
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 7 với giải bài 63 64 65 66 67 68 69 70 trang 87 88 sgk toán 7 tập 2!
“Bài tập nào khó đã có giaibaisgk.com“
