Luyện tập: Giải bài 33 34 35 36 37 trang 87 sgk Toán 6 tập 2

Nội Dung

Hướng dẫn giải Bài §6. Tia phân giác của góc, chương II – Góc, sách giáo khoa toán 6 tập hai. Nội dung bài giải bài luyện tập: giải bài 33 34 35 36 37 trang 87 sgk toán 6 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 6.

Lý thuyết

1. Tia phân giác của 1 góc là gì?

Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hại cạnh ấy hai góc bằng nhau

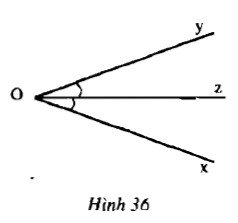
Tia Oz là tia phân giác của góc xOy thì:

+ Tia Oz nằm giữa hai tia Ox, Oy.

+ $\widehat {xOy} = \widehat {zOy}$

Hoặc $\widehat {xOz} = \widehat {zOy} = \frac{1}{2}\widehat {xOy}.$

2. Cách vẽ tia phân giác của một góc

Cách 1: Dùng thước đo góc

Cách 2: Gấp giấy

Dưới đây là Hướng dẫn giải bài luyện tập: giải bài 33 34 35 36 37 trang 87 sgk toán 6 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Luyện tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 6 kèm bài giải chi tiết bài 33 34 35 36 37 trang 87 sgk toán 6 tập 2 của bài §6 Tia phân giác của góc chương II – Góc cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 33 34 35 36 37 trang 87 sgk toán 6 tập 2

1. Giải bài 33 trang 87 sgk Toán 6 tập 2

Vẽ hai góc kề bù $xOy, yOx’$, biết $\widehat{xOy}$ = 130⁰.Gọi Ot là tia phân giác của góc xOy. Tính số đo góc $\widehat{x’Ot}$.

Bài giải:

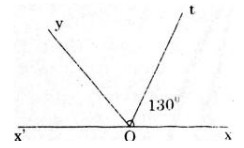
Vì $Ot$ là tia phân giác của góc $xOy$ nên:

$\widehat{xOt} = \widehat {tOy} $$= \dfrac{1}2\widehat{xOy}$ $=\dfrac{130^{0}}2=65^0$

Vì hai góc $xOy, yOx’$ kề bù nên $\widehat {xOx’} = \widehat {xOy} + \widehat {yOx’} = {180^0}$

Ta có $\widehat {xOx’} > \widehat {xOt\,\,}({180^0} > {65^0})$ nên tia $Ot$ nằm giữa hai tia $Ox$ và $Ox’$

Ta có:

$\widehat {xOt} + \widehat {x’Ot} = \widehat {xOx’} $
$\Rightarrow \widehat {x’Ot} = \widehat {xOx’} – \widehat {xOt} $$= {180^0} – {65^0} = {115^0} $

2. Giải bài 34 trang 87 sgk Toán 6 tập 2

Vẽ hai góc kề bù xOy và yOx’, biết $\widehat{xOy}$ = 100⁰. Gọi Ot là thia phân giác của góc xOy và Ot’ là tia phân giác của góc x’Oy. Tính $\widehat{x’Ot}$, $\widehat{xOt’}$, $\widehat{tOt}$

Bài giải:

Hai góc $xOy$ và $x’Oy$ là hai góc kề bù mà $\widehat{xOy}=100^0$ nên $\widehat{x’Oy}=180^0-100^0=80^0$

Vì $Ot$ là tia phân giác của góc $xOy$ nên:

$\displaystyle \widehat {xOt} = \widehat {tOy} = {{\widehat {xOy}} \over 2}$$ \displaystyle = {{{{100}^0}} \over 2} = {50^0}$

Vì $Ot’$ là tia phân giác của góc $x’Oy$ nên:

$\displaystyle \widehat {x’Ot’} = \widehat {t’Oy} $$\displaystyle = {{\widehat {x’Oy}} \over 2} = {{{{80}^0}} \over 2} = {40^0}$

– Góc $x’Ot$ và góc $xOt$ là hai góc kề bù nên:

$\widehat {x’Ot} + \widehat {xOt}=180^0$

⇒ $\widehat {x’Ot}=180^0-\widehat {xOt}=180^0-50^0=130^0$

– Góc $xOt’$ và góc $x’Ot’$ là hai góc kề bù nên:

$\widehat {xOt’} + \widehat {x’Ot’}=180^0$

⇒ $\widehat {xOt’}=180^0-\widehat {x’Ot’}=180^0-40^0=140^0$

– Góc $yOt’$ và góc $tOy$ là hai góc kề nhau nên:

$\widehat {yOt’} + \widehat {yOt}=\widehat {t’Ot}$

⇒ $\widehat {t’Ot}=50^0+40^0=90^0$

3. Giải bài 35 trang 87 sgk Toán 6 tập 2

Vẽ góc bẹt xOy. Vẽ tia phân giác Om của góc đó. Vẽ tia phân giác Oa của góc xOm. Bẽ tia phân giác Ob của góc mOy. Tính số đo góc aOb.

Bài giải:

Cách 1: Giải tương tự bài 34 ta được $\widehat{aOb}=90^0$

Ta có: Tia $Om$ là tia phân giác của góc $xOy$ nên:

$\widehat {xOm} = \widehat {yOm} = \dfrac{{\widehat {xOy}}}{2}=90^0$

Lại có: Tia $Oa$ là tia phân giác của góc $xOm$ nên ta có:

$\widehat {xOa} = \widehat {aOm} = \dfrac{{\widehat {xOm}}}{2}$ $=\dfrac{{{{90}^0}}}{2} = {45^0}$

Tia $Ob$ là tia phân giác của góc $yOm$ nên ta có:

$\widehat {bOm} = \widehat {yOb} = \dfrac{{\widehat {yOm}}}{2}$ $=\dfrac{{{{90}^0}}}{2} = {45^0}$

Ta có tia $Om$ nằm giữa hai tia $Oa$ và $Ob$ nên ta có:

$\widehat {aOb} = \widehat {aOm} + \widehat {bOm} = {45^0} + {45^0} = {90^0}$

Vậy $\widehat {aOb} = {90^0}$

Cách 2:

Tia $Oa$ là tia phân giác của góc $xOm$ nên $\widehat{ aOm}=\dfrac{\widehat{xOm}}2$

Tia $Ob$ là tia phân giác của góc $yOm$ nên $\widehat{bOm}=\dfrac{\widehat{yOm}}2$.

Tia $Om$ nằm giữa hai tia $Oa, Ob$ do đó: $\widehat{aOb}$= $\widehat{aOm}+\widehat{bOm}$

$ = \dfrac{1}{2}\left( {\widehat {xOm} + \widehat {yOm}} \right) = \dfrac{1}{2}\widehat {xOy}$

$ = \dfrac{1}{2}.180^\circ = 90^\circ $

4. Giải bài 36 trang 87 sgk Toán 6 tập 2

Cho hai tia Oy,Oz cùng nằm trên một nửa mặt phẳng có bờ chứa tia Ox. Biết:

$\widehat{ xOy}$=30⁰,$\widehat{ xOz}$=80⁰

Vẽ tia phân giác Om của góc xOy. Vẽ tia phân giác On của yOz. Tính $\widehat{mOn}$

Bài giải:

Vì hai tia $Oy, Oz$ cùng nằm trên nửa mặt phẳng bờ chứa tia $Ox$ mà $\widehat{ xOy}$< $\widehat{ xOz}$ $(30^0<80^0)$ nên tia $Oy$ nằm giữa hai tia $Ox, Oz.$

Do đó $\widehat{ xOy}$+ $\widehat{ yOz}$= $\widehat{ xOz}$

Suy ra $\widehat{ yOz}=\widehat{ xOz}-\widehat{ xOy}$$= 80^0-50^0=30^0$

Ta có tia $Om$ là tia phân giác của góc $xOy$ nên:

$\widehat {xOm} = \widehat {mOy} $$= \dfrac{{\widehat {xOy}}}{2} = \dfrac{{{{30}^0}}}{2} = {15^0}$

Tia $On$ là tia phân giác của góc $yOz$ nên:

$\widehat {yOn} = \widehat {nOz} = \dfrac{{\widehat {yOz}}}{2} $$= \dfrac{{{{50}^0}}}{2} = {25^0}$

Vì tia $Oy$ nằm giữa hai tia $Ox,Oz$ mà tia $On$ là tia phân giác góc $zOy$, tia $Om$ là tia phân giác góc $xOy$ nên $Om$ và $On$ nằm trên hai nửa mặt phẳng đối nhau bờ là tia $Oy$. Do đó tia $Oy$ nằm giữa hai tia $Om, On$, suy ra:

$\widehat{mOn}$ =$\widehat{mOy}$ + $\widehat{yOn}$ $ = {15^0} + {25^0} = {40^0}$

5. Giải bài 37 trang 87 sgk Toán 6 tập 2

Cho hai tia Oy, Oz cùng nằm trên một nửa mặt phẳng có bờ chứa tia Ox. Biết rằng $\widehat{xOy}$=30⁰, $\widehat{xOz}$= 120⁰.

a) Tính số đo góc yOz.

b) Vẽ tia phân giác Om của $\widehat{xOy}$,tia phân giác On của $\widehat{xOz}$. Tính số đo góc mOn

Bài giải:

a) Do hai tia $Oy, Oz$ cùng nằm trên một nửa mặt phẳng bờ chứa tia $Ox,$ mà: $\widehat {xOy} < \widehat {xOz}$ $(30^0<120^0)$ nên ta có tia $Oy$ nằm giữa hai tia $Ox, Oz,$ từ đó ta có:

$\widehat {xOy} + \widehat {yOz} = \widehat {xOz} $$\Rightarrow \widehat {yOz} = \widehat {xOz} – \widehat {xOy}$

$\widehat{yOz}=120^0-30^0=90^0$

b) Ta có tia $Om$ là tia phân giác của góc $xOy$ nên:

$\widehat {xOm} = \widehat {yOm} = \dfrac{{\widehat {xOy}}}{2} $$= \dfrac{{{{30}^0}}}{2} = {15^0}$

Ta có tia $On$ là tia phân giác của góc $xOz$ nên ta có:

$\widehat {xOn} = \widehat {nOz} = \dfrac{{\widehat {xOz}}}{2} $$= \dfrac{{{{120}^0}}}{2} = {60^0}$

Do hai tia $Om, On$ cùng nằm trên một nửa mặt phẳng bờ chứa tia $Ox,$ mà: $\widehat {xOm} < \widehat {xOn}$ $(15^0<60^0)$ nên ta có tia $Om$ nằm giữa hai tia $Ox, On,$ từ đó ta có:

$\widehat {xOm} + \widehat {mOn} = \widehat {xOn}$

$\Rightarrow \widehat {mOn} = \widehat {xOn} – \widehat {xOm} $$= {60^0} – {15^0} = {45^0}$

Bài trước:

Giải bài 30 31 32 trang 87 sgk toán 6 tập 2

Bài tiếp theo:

Giải bài 38 39 40 41 42 trang 91 92 93 sgk Toán 6 tập 2

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 6 với giải bài 33 34 35 36 37 trang 87 sgk toán 6 tập 2!

“Bài tập nào khó đã có giaibaisgk.com“