Luyện tập: Giải bài 21 22 23 24 25 trang 14 sgk Toán 6 tập 1

Nội Dung

Luyện tập Bài §4. Số phần tử của một tập hợp. Tập hợp con, chương I – Ôn tập và bổ túc về số tự nhiên, sách giáo khoa toán 6 tập một. Nội dung bài giải bài 21 22 23 24 25 trang 14 sgk toán 6 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần số học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 6.

Lý thuyết

1. Số phần tử của một tập hợp

Cho các tập hợp sau:

$\begin{array}{l} A = \left\{ 5 \right\}\\ B = \left\{ {x;y} \right\}\\ C = \left\{ {1;2;3;…;100} \right\}\\ N = \left\{ {0;1;2;…} \right\} \end{array}$

Ta nói rằng tập hợp A có một phần tử, tập hợp B có hai phần tử, tập hợp C có 100 phần tử, tập hợp N có vô số phần tử

Chú ý:

– Tập hợp không có phần tử nào gọi là tập hợp rỗng.

– Tập hợp rỗng được kí hiệu là $\emptyset $

Một tập hợp có thể có một phần tử, nhiều phần tử, có vô số phần tử, cũng có thể không có phần tử nào.

2. Tập hợp con

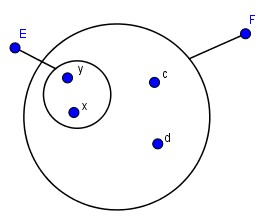
$\begin{array}{l} E = \left\{ {x,y} \right\},\\ F = \left\{ {x,y,c,d} \right\} \end{array}$

Nhận xét: Nếu mọi phần tử của tập hợp A đều thuộc tập hợp B thì tập hợp A được gọi là tập hợp con của tập hợp B.

– Ta kí hiệu $A \subset B$ hay $B \supset A$

– Đọc là A là tập hợp con của tập hợp B, hoặc A chứa trong B hoặc B chứa A.

– Nếu $A \subset B$ và $B \subset A$ thì ta nói A và B là hai tập hợp bằng nhau, kí hiệu là $A = B$

Dưới đây là Hướng dẫn giải bài 21 22 23 24 25 trang 14 sgk toán 6 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Luyện tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần số học 6 kèm bài giải chi tiết bài 21 22 23 24 25 trang 14 sgk toán 6 tập 1 của bài §4. Số phần tử của một tập hợp. Tập hợp con trong chương I – Ôn tập và bổ túc về số tự nhiên cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 21 trang 14 sgk Toán 6 tập 1

Tập hợp A = {8; 9; 10;…; 20} có 20 – 8 + 1 = 13 (phần tử)

Tổng quát: Tập hợp các số tự nhiên từ a đến b có b – a + 1 phần tử.

Hãy tính số phần tử của tập hợp sau: B = {10; 11; 12;….; 99}

Bài giải:

Số phần tử của tập hợp B là $99 – 10 + 1 = 90$.

2. Giải bài 22 trang 14 sgk Toán 6 tập 1

Số chẵn là số tự nhiên có chữ số tận cùng là 0, 2, 4, 6, 8; số lẻ là số tự nhiên có chữ số tận cùng là 1, 3, 5, 7, 9. Hai số chẵn (hoặc lẻ) liên tiếp thì hơn kém nhau 2 đơn vị.

a) Viết tập hợp C các số chẵn nhỏ hơn 10.

b) Viết tập hợp L các số lẻ lớn hơn 10 nhưng nhỏ hơn 20.

c) Viết tập hợp A ba số chẵn liên tiếp, trong đó số nhỏ nhất là 18.

d) Viết tập hợp B bốn số lẻ liên tiếp, trong đó số lớn nhất là 31.

Bài giải:

a) C = {$0; 2; 4; 6; 8$}

b) L = {$11; 13; 15; 17; 19$}

c) A = {$18; 20; 22$}

d) B = {$25; 27; 29; 31$}

3. Giải bài 23 trang 14 sgk Toán 6 tập 1

Tập hợp C = {$8; 10; 12;…;30$} có (30 – 8): 2 + 1 = 12 (phần tử)

Tổng quát:

– Tập hợp các số chẵn từ số chẵn a đến số chẵn b có (b – a) : 2 +1 phần tử.

– Tập hợp các số lẻ từ số lẻ m đến số lẻ n có (n – m) : 2 +1 phần tử.

Hãy tính số phần tử của các tập hợp sau:

D = {21; 23; 25;… ; 99}

E = {32; 34; 36; …; 96}

Bài giải:

Số phần tử của tập hợp D là $(99 – 21) : 2 + 1 = 40$.

Số phần tử của tập hợp E là $33$.

4. Giải bài 24 trang 14 sgk Toán 6 tập 1

Cho A là tập hợp các số tự nhiên nhỏ hơn 10,

B là tập hợp các số chẵn,

N* là tập hợp các số tự nhiên khác 0.

Dùng kí hiệu ⊂ để thể hiện quan hệ của mỗi tập hợp trên với tập hợp N các số tự nhiên.

Bài giải:

Vì mỗi số tự nhiên nhỏ hơn 10 đều thuộc N nên A ⊂ N.

Mỗi số chẵn cũng là một số tự nhiên nên mỗi số chẵn cũng là một phần tử của tập hợp N các số tự nhiên nên B ⊂ N. Hiển nhiên N* ⊂ N.

5. Giải bài 25 trang 14 sgk Toán 6 tập 1

Cho bảng sau (theo Niên giám năm 1999):

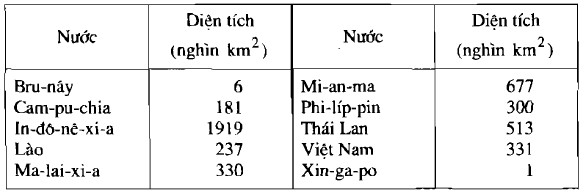
Viết tập hợp A bốn nước có diện tích lớn nhất, viết tập hợp B ba nước có diện tích nhỏ nhất.

Bài giải:

A = {In-đô-nê-xi-a; Mi-an-ma; Thái Lan; Việt Nam}.

B = {Xin-ga-po; Bru-nây; Cam-pu-chia}.

Bài trước:

Giải bài 16 17 18 19 20 trang 13 sgk toán 6 tập 1

Bài tiếp theo:

Giải bài 26 27 28 29 30 trang 16 17 sgk toán 6 tập 1

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 6 với giải bài 21 22 23 24 25 trang 14 sgk toán 6 tập 1!

“Bài tập nào khó đã có giaibaisgk.com“