Nội Dung
Luyện tập Bài §5. Quy đồng mẫu số nhiều phân số, sách giáo khoa toán 6 tập hai. Nội dung bài Giải bài 32 33 34 35 36 trang 19 20 sgk Toán 6 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần số học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 6.
Lý thuyết
1. Quy đồng mẫu hai phân số
Xét hai phân số \(\frac{-3}{5}\) và \(\frac{-5}{8}\). Ta thấy 40 là một bội chung của 5 và 8. Ta sẽ tìm hai phân số có mẫu là 40 và lần lượt bằng \(\frac{-3}{5}\) và \(\frac{-5}{8}\)
Ta có: \(\frac{-3}{5}=\frac{-3.8}{5.8}=\frac{-24}{40}\) và \(\frac{-5}{8}=\frac{-5.5}{8.5}=\frac{-25}{40}\) . Cách làm này được gọi là quy đồng mẫu hai phân số.
Hai phân số \(\frac{-3}{5}\) và \(\frac{-5}{8}\) cũng có thể được quy đồng mẫu với các mẫu chung khác chẳng hạn như: 80, 120, 1600,….
Để cho đơn giản khi quy đồng mẫu hai phân số ta thường lấy mẫu chung là BCNN của các mẫu.
2. Quy đồng mẫu nhiều phân số
Vì mọi phân số đều viết được dưới dạng phân số với mẫu dương nên ta có quy tắc:
Muốn quy đồng mẫu nhiều phân số với mẫu dương ta làm như sau:
– Bước 1: Tìm một bội chung của các mẫu (thường là BCNN) để làm mẫu chung
– Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).
– Bước 3: Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng
Ví dụ: Quy đồng mẫu các phân số: \(\frac{7}{15}\) và \(\frac{13}{6}\)
Bài giải:
Tìm BCNN: BCNN (15,6)=30
Tìm thừa số phụ: 30:15=2, 30:6=5
Nhân tử và mẫu với thừa số phụ tương ứng
Vậy: \(\frac{7}{15}=\frac{7.2}{15.2}=\frac{14}{30}\) ; \(\frac{13}{6}=\frac{13.5}{6.5}=\frac{65}{30}\)
Dưới đây là Hướng dẫn Giải bài 32 33 34 35 36 trang 19 20 sgk Toán 6 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Luyện tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần số học 6 kèm bài giải chi tiết bài 32 33 34 35 36 trang 19 20 sgk toán 6 tập 2 của bài luyện tập bài § 5 Quy đồng mẫu số nhiều phân số trong chương III – Phân số cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 32 trang 19 sgk Toán 6 tập 2
Quy đồng mẫu các phân số:
a) \(\frac{{ – 4}}{7},\frac{8}{9},\frac{{ – 10}}{{21}}\)
b) \(\frac{5}{{{2^2}.3}},\frac{7}{{{2^3}.11}}\)
Bài giải:
a) Tìm BCNN của $7, 9, 21$ để làm MSC
Do đó MSC của ba phân số là $63$
Tìm thừa số phụ của mỗi mẫu rồi nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng ta được:
Vậy: \(\frac{{ – 4}}{7}\) =\(\frac{{ – 36}}{{63}}\), \(\frac{8}{9}\) = \(\frac{{56}}{{63}}\), \(\frac{{ – 10}}{{21}}\) = \(\frac{{ – 36}}{{63}}\)
b) Tìm BCNN của \({{2^2}.3},{{2^3}.11}\) để làm MSC
Do đó MSC của ba phân số là $264$
Tìm thừa số phụ của mỗi mẫu rồi nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng ta được:
Vậy: \(\frac{5}{{{2^2}.3}} = \frac{{110}}{{264}} ,\frac{7}{{{2^3}.11}} = \frac{{21}}{{264}}\)
2. Giải bài 33 trang 19 sgk Toán 6 tập 2
Quy đồng mẫu các phân số:
a) \(\frac{3}{{ – 20}},\frac{{ – 11}}{{ – 30}},\frac{7}{{15}}\)
b) \(\frac{{ – 6}}{{ – 35}},\frac{{27}}{{ – 180}}\)
Bài giải:
a) Đổi những phân số có mẫu âm thành những phân số có mẫu dương rồi rút gọn phân số chưa tối giản.
Tìm BCNN của $20, 30, 15$ để làm MSC
Do đó MSC của ba phân số là $60$
Tìm thừa số phụ của mỗi mẫu rồi nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng ta được:
Vậy: \(\frac{3}{{ – 20}} = \frac{{ – 9}}{{60}},\frac{{ – 11}}{{ – 30}} = \frac{{22}}{{60}},\frac{7}{{15}} =\frac{{28}}{{60}}\)
b) Đổi những phân số có mẫu âm thành những phân số có mẫu dương rồi rút gọn phân số chưa tối giản ( \(\frac{{27}}{{ – 180}} = \frac{{ – 3}}{{20}}\) )
Tìm BCNN của $35, 20$ để làm MSC
Do đó MSC của ba phân số là $140$
Tìm thừa số phụ của mỗi mẫu rồi nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng ta được:
Vậy: \(\frac{{ – 6}}{{ – 35}} = \frac{{24}}{{140}},\frac{{27}}{{ – 180}} = \frac{{ – 21}}{{140}}\)
3. Giải bài 34 trang 20 sgk Toán 6 tập 2
Quy đồng mẫu các phân số:
a) \(\frac{{ – 5}}{5},\frac{8}{7}\)
b) \(3,\frac{{ – 3}}{5},\frac{{ – 5}}{6}\)
c) \(\frac{{ – 9}}{7},\frac{{ – 19}}{{15}}, – 1\)
Bài giải:
a) Vì \(\frac{{ – 5}}{5} = – 1\) nên \(\frac{{ – 5}}{5} = \frac{{ – 7}}{7}\)
b) Vì \(3 = \frac{{ 3}}{1} = \frac{{3.30}}{{1.30}} = \frac{{90}}{{30}}\)
Nên áp dụng công thức quy đồng mẫu số 3 phân số ta có:
\(3 = \frac{3}{1} = \frac{{3.30}}{{1.30}} = \frac{{90}}{{30}},\frac{{ – 3}}{5} = \frac{{ – 3.6}}{{5.6}} = \frac{{ – 18}}{{30}},\frac{{ – 5}}{6} = \frac{{ – 5.5}}{{6.5}} = \frac{{ – 25}}{{30}}\)
c) Làm tương tự như câu b) ta có:
\(\frac{{ – 9}}{7} = \frac{{ – 9.15}}{{7.15}} = \frac{{ – 135}}{{105}};\frac{{ – 19}}{{15}} = \frac{{ – 19.7}}{{15.7}} = \frac{{ – 133}}{{105}}, – 1 = \frac{{ – 105}}{{105}}\)
4. Giải bài 35 trang 20 sgk Toán 6 tập 2
Rút gọn rồi quy đồng mẫu các phân số:
a) \(\frac{{ – 15}}{{90}};\frac{{120}}{{600}};\frac{{ – 75}}{{150}}\)
b) \(\frac{{54}}{{ – 90}};\frac{{ – 180}}{{288}};\frac{{60}}{{ – 135}}\)
Bài giải:
a) Rút gọn:
\(\frac{{ – 15}}{{90}} = – \frac{1}{6};\frac{{120}}{{600}} = \frac{1}{5};\frac{{ – 75}}{{150}} = \frac{{ – 1}}{2}\)
$BCNN (6,5,2) =30$
Do đó:
\(\begin{array}{l}\frac{{ – 15}}{{90}} = – \frac{1}{6} = – \frac{{1.5}}{{6.5}} = \frac{{ – 5}}{{30}}\\\frac{{120}}{{600}} = \frac{1}{5} = \frac{{1.6}}{{5.6}} = \frac{6}{{30}}\\\frac{{ – 75}}{{150}} = \frac{{ – 1}}{2} = \frac{{ – 1.15}}{{2.15}} = \frac{{ – 15}}{{30}}\end{array}\)
b) Rút gọn:
\(\frac{{54}}{{ – 90}} = \frac{{ – 3}}{5};\frac{{ – 180}}{{288}} = \frac{{ – 5}}{8};\frac{{60}}{{ – 135}} = \frac{4}{{ – 9}}\)
$BCNN (5,8,9) = 360$
Do đó:
\(\begin{array}{l}\frac{{54}}{{ – 90}} = \frac{{ – 3}}{5} = \frac{{( – 3).72}}{{5.72}} = \frac{{ – 216}}{{360}}\\\frac{{ – 180}}{{288}} = \frac{{ – 5}}{8} = \frac{{( – 5).45}}{{8.45}} = \frac{{ – 225}}{{360}}\\\frac{{60}}{{ – 135}} = \frac{{ – 4}}{9} = \frac{{( – 4).40}}{{9.40}} = \frac{{ – 160}}{{360}}\end{array}\)
5. Giải bài 36 trang 20 sgk Toán 6 tập 2
Đố vui: Hai bức ảnh dưới đây chụp di tích nào?

Cho các dãy phân số sau:
\(N.{1 \over 4},{3 \over {10}},{2 \over 5}, \ldots \) \(M.{2 \over 3},{3 \over 4},{5 \over 6}, \ldots\)
\(H.{1 \over 6},{1 \over 4},{1 \over 3}, \ldots \) \(S.{2 \over 9},{5 \over {18}},{1 \over 3}, \ldots\)
\(Y.{1 \over {20}},{1 \over 8},{1 \over 5}, \ldots \) \(A.{1 \over 7},{5 \over {14}},{4 \over 7}, \ldots\)
\(O.{1 \over {20}},{1 \over 8},{1 \over 5}, \ldots \) \(I.{1 \over {18}},{2 \over 9},{7 \over {18}}, \ldots \)
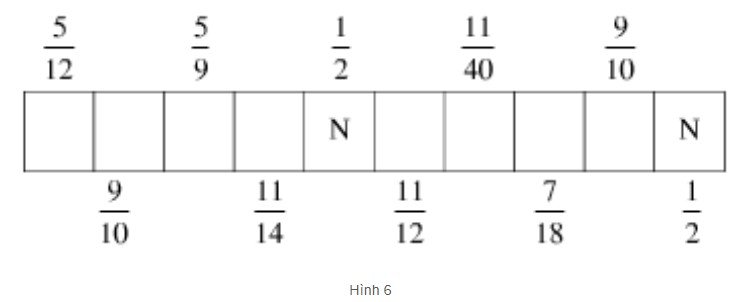
Hãy quy đồng mẫu các phân số của từng dãy rồi đoán nhận phận số thứ tư của dãy đó; viết nó dưới dạng tối giản rồi viết chữ cái ở dãy đó vào ô tương ứng với phân số ấy ở hình 6. Khi đó, em sẽ biết được hai địa danh của Việt Nam được UNESCO công nhận là di sản văn hóa thế giới vào năm 1999.
Chẳng hạn, ở dãy đầu có ghi chữ N, quy đồng mẫu ta được \({2 \over {10}},{3 \over {10}},{4 \over {10}}\) nên phân số thứ tư là \({5 \over {10}}\). Nó có dạng tối giản \({1 \over 2}\) , do đó ta điền chữ N vào hai ô ứng với số \({1 \over 2}\) trên hình 6.
Bài giải:
Ta phải viết tiếp vào dãy số như sau:
\(N \ldots ,{1 \over 2};\) \(M \ldots ,{{11} \over {12}}\) \(H \ldots ,{5 \over {12}}\) \(S \ldots ,{5 \over {18}}\)
\(Y \ldots ,{1 \over 2};\) \(A \ldots ,{{11} \over {12}}\) \(O \ldots ,{5 \over {12}}\) \(I \ldots ,{5 \over {18}}\)
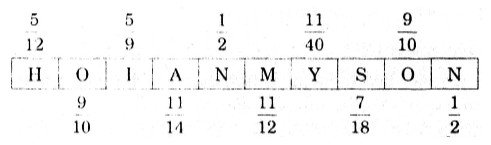
Hai di tích được UNESCO công nhận là di sản văn hoá thế giới là: Hội An, Mỹ Sơn.
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 6 khác
- Để học tốt môn Vật lí lớp 6
- Để học tốt môn Sinh học lớp 6
- Để học tốt môn Ngữ văn lớp 6
- Để học tốt môn Lịch sử lớp 6
- Để học tốt môn Địa lí lớp 6
- Để học tốt môn Tiếng Anh lớp 6
- Để học tốt môn Tiếng Anh lớp 6 thí điểm
- Để học tốt môn Tin học lớp 6
- Để học tốt môn GDCD lớp 6
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 6 với Giải bài 32 33 34 35 36 trang 19 20 sgk Toán 6 tập 2!
“Bài tập nào khó đã có giaibaisgk.com“
