Hướng dẫn Giải bài 1 2 3 4 5 6 7 8 9 10 11 trang 113 114 sgk Hình học 11

Nội Dung

Hướng dẫn giải Bài §4. Hai mặt phẳng vuông góc, Chương III. Vectơ trong không gian. Quan hệ vuông góc trong không gian, sách giáo khoa Hình học 11. Nội dung bài giải bài 1 2 3 4 5 6 7 8 9 10 11 trang 113 114 sgk Hình học 11 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập hình học có trong SGK để giúp các em học sinh học tốt môn toán lớp 11.

Lý thuyết

1. Góc giữa hai mặt phẳng

a) Định nghĩa

Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.

Nhận xét:

Nếu hai mặt phẳng song song hoặc trùng nhau thì ta nói rằng góc giữa hai mặt phẳng đó bằng 0^o.

b) Cách xác định góc giữa hai mặt phẳng cắt nhau

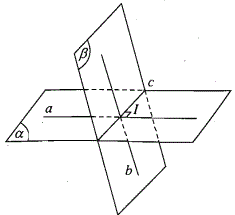
Cho hai mặt phẳng $(α)$ và $(β)$: $(α) \cap \left( β \right) = c$

Lấy $I$ bất kì thuộc $c$.

Trong $(α)$ qua $I$ kẻ $a \bot c$.

Trong $(β)$ qua $I$ kẻ $b \bot c$.

Khi đó góc giữa hai mặt phẳng $(α), (β)$ là góc giữa hai đường thẳng $a$ và $b$.

c) Diện tích hình chiếu của một đa giác

Với $S$ là diện tích đa giác nằm trong $(α), S’$ là diện tích hình chiếu vuông góc của đa giác đó trên $(β)$, $\varphi$ là góc giữa $(α)$ và $(β)$ ta có:

$S’=S.\cos \varphi$.

2. Hai mặt phẳng vuông góc

a) Định nghĩa

Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng $90^0$.

b) Các định lý

Định lí 1: Điều kiện cần và đủ để hai mặt phẳng vuông góc với nhau là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.

$\left\{ \begin{array}{l} a \bot mp(P)\\ a \subset mp(Q) \end{array} \right. \Rightarrow mp(Q) \bot mp(P)$

Hệ quả 1: Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến thì vuông góc với mặt phẳng kia.

$\left\{ \begin{array}{l} (P) \bot (Q)\\ (P) \cap (Q) = d\\ a \subset (P),a \bot d \end{array} \right. \Rightarrow a \bot (Q)$

Hệ quả 2: Cho hai mặt phẳng (P) và (Q) vuông góc với nhau. Nếu từ một điểm thuộc mặt phẳng (P) ta dựng một đường thẳng vuông góc với mặt phẳng (Q) thì đường thẳng này nằm trong mặt phẳng (P).

$\left\{ \begin{array}{l} (P) \bot (Q)\\ A \in (P)\\ A \in a\\ a \bot (Q) \end{array} \right. \Rightarrow a \subset (P)$

Định lí 2: Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.

$\left\{ \begin{array}{l} (P) \cap (Q) = a\\ (P) \bot (R)\\ (Q) \bot (R) \end{array} \right. \Rightarrow a \bot (R)$

3. Hình lăng trụ đứng, hình hộp chữ nhật, hình lập phương

a) Hình lăng trụ đứng

Hình lăng trụ đứng là hình lăng trụ có cạnh bên vuông góc với đáy.

Nhận xét: Các mặt bên của hình lăng trụ đứng là hình chữ nhật và vuông góc với mặt đáy.

b) Hình lăng trụ đều

Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.

Nhận xét: Các mặt bên của hình lăng trụ đều là những hình chữ nhật bằng nhau và vuông góc với mặt đáy.

c) Hình hộp đứng

Hình hộp đứng là hình lăng trụ đứng có đáy là hình bình hành.

Nhận xét: Trong hình hộp đứng bốn mặt bên đều là hình chữ nhật.

d) Hình hộp chữ nhật

Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.

Nhận xét: Tất cả 6 mặt của hình hộp chữ nhật đều là hình chữ nhật.

e) Hình lập phương

Hình lập phương là hình hộp chữ nhật có tất cả các cạnh bằng nhau.

4. Hình chóp đều và hình chóp cụt đều

a) Hình chóp đều

Một hình chóp được gọi là hình chóp đều nếu đáy của nó là đa giác đều và các cạnh bên bằng nhau.

Nhận xét:

– Đường vuông góc với mặt đáy kẻ từ đỉnh gọi là đường cao của hình chóp.

– Một hình chóp là hình chóp đều đáy của nó là đa giác đều và chân đường cao của hình chóp trùng với tâm của đáy.

– Một hình chóp là hình chóp đều đáy của nó là đa giác đều và các cạnh bên tạo voéi mặt đáy các góc bằng nhau.

b) Hình chóp cụt đều

Khi cắt hình chóp đều bởi 1 mặt phẳng song song với đáy để được 1 hình chóp cụt thì hình chóp cụt đó được gọi là hình chóp cụt đều.

Nhận xét:

– Hai đáy của hình chóp cụt đều là 2 đa giác đều đồng dạng với nhau.

– Đoạn nối tâm 2 đáy được gọi là đường cao của hình chóp cụt đều.

– Trong hình chóp cụt đều các mặt bên là những hình thang cân bằng nhau.

Dưới đây là phần trả lời các câu hỏi và bài tập trong mục hoạt động của học sinh trên lớp sgk Hình học 11.

Câu hỏi

1. Trả lời câu hỏi 1 trang 109 sgk Hình học 11

Cho hai mặt phẳng $(α)$ và $(β)$ vuông góc với nhau và cắt nhau theo giao tuyến $d$. Chứng minh rằng nếu có một đường thẳng $Δ$ nằm trong $(α)$ và $Δ$ vuông góc với $d$ thì $Δ$ vuông góc với $(β)$.

Trả lời:

$Δ$ nằm trong $(α)$ và $Δ$ vuông góc với $d ⇒ Δ$ cắt $d$ tại $A$

Từ $A$, vẽ đường thẳng $a$ thuộc $(β)$ và $a ⊥ d$

Vì $(α) ⊥ (β)$ nên góc giữa $Δ$ và $a$ là $90^0$ hay $Δ ⊥ a$

$⇒ Δ ⊥ (d,a)$ hay $Δ ⊥ (β)$

2. Trả lời câu hỏi 2 trang 109 sgk Hình học 11

Cho tứ diện $ABCD$ có ba cạnh $AB, AC, AD$ đôi một vuông góc với nhau. Chứng minh rằng các mặt phẳng $(ABC), (ACD), (ADB)$ cũng đôi một vuông góc với nhau.

Trả lời:

$AB ⊥ AC, AB ⊥ AD$ nên $AB ⊥ (AC, AD)$ hay $AB ⊥ (ACD)$ (theo định lí)

$AB ∈ (ABC)$ nên $(ABC) ⊥ (ACD)$ (theo định lí 1)

$AB ∈ (ADB)$ nên $(ADB) ⊥ (ACD)$

$AD ⊥ AC, AD ⊥ AB$ nên $AD ⊥ (AC, AB)$ hay $AD ⊥ (ABC)$

$AD ∈ (ADB)$ nên $(ADB) ⊥ (ABC)$

3. Trả lời câu hỏi 3 trang 109 sgk Hình học 11

Cho hình vuông $ABCD$. Dựng đoạn $AS$ vuông góc với mặt phẳng chứa hình vuông $ABCD$.

a) Hãy nêu tên các mặt phẳng lần lượt chứa các đường thẳng $SB, SC, SD$ và vuông góc với mặt phẳng $(ABCD)$

b) Chứng minh rằng mặt phẳng $(SAC)$ vuông góc với mặt phẳng $(SBD)$

Trả lời:

a) $SA ⊥ (ABCD), SA ∈ (SAB)$ ⇒ $(SAB) ⊥ (ABCD)$

$SA ⊥ (ABCD), SA ∈ (SAD)$ ⇒ $(SAD) ⊥ (ABCD)$

$SA ⊥ (ABCD)$ ⇒ $SA ⊥ BD ∈ (ABCD)$ và $BD ⊥ AC$ (hai đường chéo hình vuông)

$⇒ BD ⊥ (SA,AC)$ ⇒ $BD ⊥ (SAC)$ mà $BD ∈(ABCD)$ nên $(SAC) ⊥ (ABCD)$

b) $BD ⊥ (SAC)$ mà $BD ∈(SBD)$ nên $(SAC) ⊥ (SBD)$

4. Trả lời câu hỏi 4 trang 111 sgk Hình học 11

Cho biết mệnh đề nào sau đây là đúng?

a) Hình hộp là hình lăng trụ đứng.

b) Hình hộp chữ nhật là hình lăng trụ đứng.

c) Hình lăng trụ là hình hộp.

d) Có hình lăng trụ không phải là hình hộp.

Trả lời:

Hình hộp là hình lăng trụ tứ giác có đáy là hình bình hành.

Từ đó ta thấy,

a) sai: vì cách cạnh bên của hình hộp chưa chắc vuông góc với đáy.

b) đúng.

c) sai: vì nếu đáy của lăng trụ nếu không phải là hình bình hành thì sẽ không phải hình hộp.

d) đúng: vì các hình lăng trụ tam giác, tứ giác thường,… đều không là hình hộp.

5. Trả lời câu hỏi 5 trang 111 sgk Hình học 11

Sáu mặt của hình hộp chữ nhật có phải là những hình chữ nhật không?

Trả lời:

Sáu mặt của hình hộp chữ nhật là những hình chữ nhật.

6. Trả lời câu hỏi 6 trang 112 sgk Hình học 11

Chứng minh rằng hình chóp đều có các mặt bên là những tam giác cân bằng nhau

Trả lời:

Xét trường hợp Hình chóp tứ giác đều

Ta có đáy là hình vuông $ABCD$

Tâm hình vuông $ABCD$ là $O$ (giao điểm $2$ đường chéo)

Gọi $M$ là trung điểm $BC ⇒ OM // AB$ hay $OM ⊥ BC$

Theo định nghĩa hình chóp đều: $SO ⊥ (ABCD) ⇒ SO ⊥ BC$

$⇒ BC ⊥(SO,OM)$ ⇒ $BC⊥(SOM) ⇒ BC⊥SM$

Tam giác $SBC$ có $SM$ vừa là đường cao vừa là trung tuyến $⇒ SBC$ cân tại $S$

Chứng minh tương tự ⇒ Các mặt bên là những tam giác cân bằng nhau

Trường hợp hình chóp đều khác, chứng minh tương tự.

7. Trả lời câu hỏi 7 trang 112 sgk Hình học 11

Có tồn tại một hình chóp tứ giác $S.ABCD$ có hai mặt bên $(SAB)$ và $(SCD)$ cùng vuông góc với mặt phẳng đáy hay không?

Trả lời:

Không tồn tại một hình chóp tứ giác $S.ABCD$ có hai mặt bên $(SAB)$ và $(SCD)$ cùng vuông góc với mặt phẳng đáy.

Dưới đây là phần Hướng dẫn giải bài 1 2 3 4 5 6 7 8 9 10 11 trang 113 114 sgk Hình học 11. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập hình học 11 kèm bài giải chi tiết bài 1 2 3 4 5 6 7 8 9 10 11 trang 113 114 sgk Hình học 11 của Bài §4. Hai mặt phẳng vuông góc trong Chương III. Vectơ trong không gian. Quan hệ vuông góc trong không gian trong mặt phẳng cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 6 7 8 9 10 11 trang 113 114 sgk Hình học 11

1. Giải bài 1 trang 113 sgk Hình học 11

Cho ba mặt phẳng $(\alpha ),(\beta ),(\gamma )$ những mệnh đề nào sau đây đúng?

a) Nếu $(α) ⊥ (β)$ và $(α) // (\gamma)$ thì $(β) ⊥ (\gamma )$

b) Nếu $(α) ⊥ (β)$ và $(α) ⊥ (\gamma)$ thì $(β) // (\gamma )$

Bài giải:

a) Đúng.

Vì: gọi $m$ là đường thẳng vuông góc $(\alpha )$, $n$ là đường thẳng vuông góc với $(\beta )$.

⇒ $\widehat{(\alpha ),(\beta )}=\widehat{m,n}$

Do $(α) ⊥ (β)$ ⇒ $\widehat{(\alpha ),(\beta )}=\widehat{m,n}=90^0$

Lại có: $(\alpha )$ // $(\gamma )$ nên m vuông góc với $(\gamma )$

⇒ $\widehat{(\beta ),(\gamma )}=\widehat{m,n}=90^0$

⇒ (β) ⊥ $(\gamma )$

b) Sai, vì hai mặt phẳng $(β), (\gamma )$ cùng vuông góc với $(α)$ có thể song song hoặc cắt nhau.

2. Giải bài 2 trang 113 sgk Hình học 11

Cho hai mặt phẳng $(\alpha)$ và $(\beta)$ vuông góc với nhau. Người ta lấy trên giao tuyến $\Delta$ của hai mặt phẳng đó hai điểm $A$ và $B$ sao cho $AB=8cm$. Gọi $C$ là một điểm trên $(\alpha)$ và $D$ là một điểm trên $(\beta)$ sao cho $AC$ và $BD$ cùng vuông góc với giao tuyến $\Delta$ và $AC=6cm$, $BD=24cm$. Tính độ dài đoạn $CD$.

Bài giải:

Ta có:

$\left. \matrix{
(\alpha ) \bot (\beta ) \hfill \cr
AC \bot \Delta \hfill \cr
AC \subset (\alpha ) \hfill \cr} \right\} \Rightarrow AC \bot (\beta )$

Do đó $AC\bot AD$ hay tam giác $ACD$ vuông tại $A$

Áp dụng định lí Pytago vào tam giác $ACD$ ta có:

${CD^2} = {AC^2} + {AD^2}(1)$

Theo giả thiết $BD$ vuông góc với giao tuyến nên $BD\bot AB$ hay tam giác $ABD$ vuông tại $B$.

Áp dụng định lí Pytago vào tam giác $ABD$ ta được:

${AD^2} = {AB^2} + {BD^2}(2)$

Từ (1) và (2) suy ra: ${CD^2} = {AC^2} + {AB^2} + {BD^2} = {6^2} + {8^2} + {24^2} = 676$

$ \Rightarrow DC = \sqrt {676} = 26cm$

3. Giải bài 3 trang 113 sgk Hình học 11

Trong mặt phẳng $(\alpha)$ cho tam giác $ABC$ vuông ở $B$. Một đoạn thẳng $AD$ vuông góc với $(\alpha)$ tại $A$. Chứng minh rằng:

a) $\widehat {ABD}$ là góc giữa hai mặt phẳng $(ABC)$ và $(DBC)$;

b) Mặt phẳng $(ABD)$ vuông góc với mặt phẳng $(BCD)$;

c) $HK//BC$ với $H$ và $K$ lần lượt là giao điểm của $DB$ và $DC$ với mặt phẳng $(P)$ đi qua $A$ và vuông góc với $DB$.

Bài giải:

a) Tam giác $ABC$ vuông tại $B(gt)$ nên $AB\bot BC$ (1)

$AD$ vuông góc với $(\alpha)$ (gt) nên $AD\bot BC$ (2)

Từ (1) và (2) ta có:

$\left.\begin{matrix} AB& \perp BC \\ AD& \perp BC \\ AB& \cap AD \end{matrix}\right\}\Rightarrow BC\perp (ABD)$

mà $BD\subset (ABD)$ suy ra $BC\bot BD$

Do đó: $(ABC)\cap (DBC)=BC$, $AB\bot BC$, $BC\bot BD$

⇒ Góc giữa hai mặt phẳng $(ABC)$ và $(DBC)$ là $\widehat{AB,BD}=\widehat{ABD}$ (đpcm)

b) Ta có:

$\left. \matrix{
BC \bot (ABD) (cmt) \hfill \cr
BC \subset (BCD) \hfill \cr} \right\} \Rightarrow (ABD) \bot (BCD)$ (đpcm)

c) Ta có:

$HK\subset (P)$ mà $(P)$ đi qua $A$ và vuông góc với $BD$ nên $HK\bot BD$

Trong $(BCD)$ có: $HK\bot BD$ và $BC\bot BD$ nên suy ra $HK// BC$.

4. Giải bài 4 trang 114 sgk Hình học 11

Cho hai mặt phẳng $(\alpha)$, $(\beta)$ cắt nhau và một điểm $M$ không thuộc $(\alpha)$ và không thuộc $(\beta)$. Chứng minh rằng qua điểm $M$ có một và chỉ một mặt phẳng $(P)$ vuông góc với $(\alpha)$ và $(\beta)$. Nếu $(\alpha)$ song song với $(\beta)$ thì kết quả trên sẽ thay đổi như thế nào?

Bài giải:

Điều kiện cần: Qua $M$ có một mặt phẳng $(P)$ vuông góc với $(\alpha)$ và $(\beta)$

Gọi $a=(\alpha)\cap (\beta)$. Gọi $(P)$ là mặt phẳng đi qua $M$ và vuông góc với $a$.

Vì $a\subset (\alpha)$ nên $(P)\bot (\alpha)$, $a\subset (\beta)$ nên $(P)\bot(\beta)$ (Tính chất: mặt phẳng vuông góc với giao tuyến của hai mặt phẳng thì vuông góc với từng mặt phẳng)

Như vậy qua $M$ có mặt phẳng $(P)$ vuông góc với $(\alpha)$ và $(\beta)$.

Điều kiện đủ: Mặt phẳng $(P)$ là duy nhất.

Nếu có $(P)$ đi qua $M$ và vuông góc với $(\alpha)$ và $(\beta)$ thì $(P)\bot a$. Do tính duy nhất của mặt phẳng đi qua một điểm và vuông góc với một đường thẳng cho trước nên $(P)$ duy nhất.

Nếu $(\alpha)//(\beta)$ thì: gọi $d$ là đường thẳng đi qua $M$ và vuông góc với $(\alpha)$ khi đó ta có $d\bot (\beta)$. Như vậy mọi mặt phẳng chứa $d$ đều vuông góc với $(\alpha)$ và $(\beta)$.

Do đó khi $(\alpha)//(\beta)$ thì có vô số mặt phẳng $(P)$ đi qua $M$ và vuông góc với $(\alpha)$ và $(\beta)$.

5. Giải bài 5 trang 114 sgk Hình học 11

Cho hình lập phương $ABCD.A’B’C’D’$. Chứng minh rằng:

a) Mặt phẳng $(AB’C’D)$ vuông góc với mặt phẳng $(BCD’A’)$;

b) Đường thẳng $AC’$ vuông góc với mặt phẳng $(A’BD)$.

Bài giải:

a) Ta có: $BC ⊥ (ABB’A’)$ (tính chất hình lập phương), $AB’\subset (ABB’A’)$

$\Rightarrow BC ⊥ AB’$;

Mà $BA’ ⊥ AB’$ (đường chéo hình vuông ABB’A’)

$\left.\begin{matrix} BC& \perp AB’ \\ A’B& \perp AB’ \\ BC& \cap A’B \end{matrix}\right\}\Rightarrow AB’\perp (BCD’A’)$

Ta có $AB’ ⊂ (AB’C’D)$ nên ($AB’C’D) ⊥ (BCD’A’)$.

b) Ta có:

$AA’\bot(ABCD) \Rightarrow AA’\bot BD$

Mà $BD\bot AC,AC\cap AA’\Rightarrow BD\bot (ACC’A’)$

$AC’\subset(ACC’A’)$ nên suy ra $BD\bot AC’$ (1)

$AB\bot (ADD’A’)\Rightarrow AB\bot A’D $

Mà $AD’\bot A’D\Rightarrow A’D\bot (ABC’D’)$

Ta có $AC’\subset (ABC’D’)\Rightarrow AC’\bot A’D$ (2)

Từ (1) và (2) ta có:

$\left.\begin{matrix} BD& \perp A’C \\ AC’& \perp A’D \\ BD& \cap A’D \end{matrix}\right\}\Rightarrow AC’\perp (A’BD)$

6. Giải bài 6 trang 114 sgk Hình học 11

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là một hình thoi cạnh $a$ và có $SA = SB = SC = a$. Chứng minh rằng:

a) Mặt phẳng $(ABCD)$ vuông góc với mặt phẳng $(SBD)$;

b) Tam giác $SBD$ là tam giác vuông.

Bài giải:

a) Gọi $O$ là giao điểm của hai đường chéo $AC$ và $BD$

Theo tính chất của hình thoi thì $O$ là trung điểm của $AC,BD$

Tam giác cân $SAC$ có $SA=SC(gt)$

⇒ $\Delta SAC$ cân tại $S$ có $SO$ vừa là đường trung tuyến đồng thời là đường cao.

⇒ $SO\bot AC$ (1)

Mặt khác $ABCD$ là hình thoi nên $AC\bot BD$ (2)

Từ (1) và (2) suy ra:

$\left.\begin{matrix} SO& \perp AC \\ BD& \perp AC \\ SO& \cap BD \end{matrix}\right\}\Rightarrow AC\perp (SBD)$

Mà $AC\subset (ABCD)\Rightarrow (ABCD)\bot (SBD)$

b) Xét $\Delta SAC và \Delta BAC$ có:

$AC chung$

$SA=AB(=a);SC=BC=(a)$

⇒ $∆SAC = ∆BAC (c.c.c)$

Do đó các đường trung tuyến ứng với các đỉnh tương ứng của hai tam giác bằng nhau

⇒ $SO = BO$

Vì $O$ là trung điểm của $BD$ nên $OB=OD={1\over 2}.BD$

Suy ra $SO={1\over 2} .BD$

⇒ Tam giác $SBD$ vuông tại $S$ (Đường trung tuyến ứng với một cạnh của tam giác và bằng nửa cạnh ấy thì tam giác đó là tam giác vuông)

7. Giải bài 7 trang 114 sgk Hình học 11

Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ có $AB = a, BC = b, CC’ = c$.

a) Chứng minh rằng mặt phẳng $(ADC’B’)$ vuông góc với mặt phẳng $(ABB’A’)$.

b) Tính độ dài đường chéo $AC’$ theo $a, b, c$.

Bài giải:

a) Ta có: $DA ⊥ (ABB’A’)$ (tính chất hình hộp)

$DA ⊂ (ADC’B’)$

$\Rightarrow (ADC’B’) \bot(ABB’A’)$.

b) Ta có: $CC’ ⊥ (ABCD)$ (tính chất hình hộp)

$AC ⊂ (ABCD)$

$\Rightarrow AC \perp CC’$

⇒ Tam giác $ACC’$ vuông tại $C$

⇒ $AC^2+CC’^2=AC’^2$ (định lý Pytago) (1)

Mặt khác, $\Delta ABC$ vuông tại B ⇒ $AB^2+BC^2=AC^2$ (định lý Pytago)

Thay vào (1) ta được:

$AC’ = \sqrt {AC^2 + CC’^2} = \sqrt {AB^2 + BC^2 + CC’^2}$ $=\sqrt{a^{2}+b^{2}+c^{2}}.$

8. Giải bài 8 trang 114 sgk Hình học 11

Tính độ dài đường chéo của một hình lập phương cạnh $a$.

Bài giải:

Hình lập phương $ABCD.A’B’C’D’$ có cạnh $a$, các đường chéo $AC’,A’C,BD’,B’D$ bằng nhau.

Ta chỉ cần tính đại diện một đường chéo, chẳng hạn $AC’$.

Ta có: $CC’ ⊥ (ABCD)$ (tính chất hình hộp)

$AC ⊂ (ABCD)$

$\Rightarrow AC \perp CC’$

⇒ Tam giác $ACC’$ vuông tại $C$

⇒ $AC^2+CC’^2=AC’^2$ (định lý Pytago) (1)

Mặt khác, $\Delta ABC$ vuông tại B ⇒ $AB^2+BC^2=AC^2$ (định lý Pytago)

Thay vào (1) ta được:

$AC’ = \sqrt {AC^2 + CC’^2} = \sqrt {AB^2 + BC^2 + CC’^2}$ $=\sqrt{a^{2}+a^{2}+a^{2}}.$ $=a\sqrt {3}$

9. Giải bài 9 trang 114 sgk Hình học 11

Cho hình chóp tam giác đều $S.ABC $ có $SH$ là đường cao. Chứng minh $SA ⊥ BC$ và $SB ⊥ AC$

Bài giải:

Chứng minh $SA\perp BC$

Vì $S.ABC$ là chóp đều có $SH$ là đường cao nên $SH\perp (ABC)$ tại $H$ là trực tâm của $\Delta ABC$

$SH\perp (ABC)$, $BC\subset (ABC)$ $\Rightarrow SH \perp BC$

VÌ $H$ là trực tâm của $\Delta ABC$ nên $AH\perp BC$

Ta có:

$\left.\begin{matrix} SH& \perp BC \\ AH& \perp BC \\ SH& \cap AH \end{matrix}\right\}\Rightarrow BC\perp (SAH)$

mà $SA\subset (SAH)$

$\Rightarrow BC \perp SA$

Chứng minh $AC\perp SB$

Vì $H$ là trực tâm tam giác ABC nên $BH\perp AC$.

Lại có: $SH\perp (ABC) (cmt)$

⇒ $SH\perp AC$.

Ta có:

$\left.\begin{matrix} SH& \perp AC \\ BH& \perp AC \\ SH& \cap BH \end{matrix}\right\}\Rightarrow AC\perp (SBH)$

⇒ $AC\perp SB$

10. Giải bài 10 trang 114 sgk Hình học 11

Cho hình chóp tứ giác đều $S.ABCD$ có các cạnh bên và cạnh đáy đều bằng $a$. Gọi $O$ là tâm của hình vuông $ ABCD$.

a) Tính độ dài đoạn thẳng $SO$.

b) Gọi $M$ là trung điểm của đoạn $SC$. Chứng minh hai mặt phẳng $(MBD)$ và $(SAC)$ vuông góc với nhau.

c) Tính độ dài đoạn $OM$ và tính góc giữa hai mặt phẳng $(MBD)$ và $(ABCD)$.

Bài giải:

a) $ABCD$ là hình vuông cạnh $a$

⇒ Tam giác $ABC$ vuông tại $B$

⇒ $AC=\sqrt{AB^2+BC^2}=\sqrt{a^2+a^2}=a\sqrt{2}$

Lại có $O$ là tâm hình vuông $ABCD(gt)$ nên $O$ là trung điểm của $AC$

⇒ $OA=\frac{1}{2}.AC=a.\frac{\sqrt{2}}{2}$

Hình chóp tứ giác đều nên $SO\bot (ABCD)$. Do đó $SO\bot AC$

Xét tam giác $SOA$ vuông tại $O$: có $SA^2=OA^2+SO^2$ (định lý Pitago)

⇒ $SO = \sqrt{SA^{2}-AO^{2}}=\frac{a\sqrt{2}}{2}.$

b) Ta có: $BD\bot AC$ (tính chất hình vuông) (1)

Vì $SO\perp (ABCD), BD\subset (ABCD)⇒SO\perp BD$ (2)

Từ (1), (2) và $AC \cap SO$ suy ra: $BD \bot (SAC)$,

Mà $BD ⊂ (MBD)$ do đó $(MBD) ⊥ (SAC) (đpcm)$.

c) Xét $\Delta SCD$ và $\Delta SCB$ có:

$SC$ chung

$SD=SB(=a);CD=CB(=a)$

⇒ $\Delta SCD\sim \Delta SCB(c.c.c)$

⇒ $DM=BM$ (trung tuyến tương ứng của 2 tam giác bằng nhau)

suy ra $DM=BM$ suy ra tam giác $BDM$ cân tại $M$

⇒ $OM$ vừa là trung tuyến đồng thời là đường cao nên $OM\bot BD$

Ta có:

$\left. \matrix{
(MBD) \cap (ABCD) = BD \hfill \cr
OM \bot BD \hfill \cr
OC \bot BD \hfill \cr} \right\} $

$\Rightarrow $ góc giữa hai mặt phẳng $(MBD)$ và $(ABCD)$ là $\widehat {MOC}$

Trong $\Delta SOC$ vuông tại O có $OM$ là trung tuyến ứng với cạnh huyền $SC$

Suy ra: $OM=MC=\frac{SC}{2}=\frac{a}{2}$ hay tam giác $OMC$ vuông cân tại $M$

Do đó: $(\widehat{(MBD);(ABCD)})=(\widehat{MOC})=45^{0}.$

11. Giải bài 11 trang 114 sgk Hình học 11

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là một hình thoi tâm $I$ cạnh $a$ và có góc $A$ bằng $60^{0},$ cạnh $SC=\frac{a\sqrt{6}}{2}$ và $SC$ vuông góc với mặt phẳng $(ABCD)$.

a) Chứng minh mặt phẳng $(SBD)$ vuông góc với mặt phẳng $(SAC)$.

b) Trong tam giác $SCA$ kẻ $IK$ vuông góc với $SA$ tại $K$. Hãy tính độ dài $IK$

c) Chứng minh $\widehat{BKD}=90^{0}$ và từ đó suy ra mặt phẳng $(SAB)$ vuông góc với mặt phẳng $(SAD)$.

Bài giải:

a) $SC$ vuông góc với mặt phẳng $(ABCD)$ suy ra $SC\bot BD$ (1)

$ABCD$ là hình thoi nên $AC\bot BD$ (2)

Từ (1) và (2) suy ra $BD ⊥ (SAC)$

$BD\subset (SBD)\Rightarrow (SBD) ⊥ (SAC)$.

b) Xét tam giác vuông $ABI$ có: $cos\widehat{IAB}=\frac{AI}{AB} ⇒ AI=AB.cos\widehat{IAB}=AB.\frac{1}{2}.\widehat{IAB}$

⇒ $AI=AB.\cos 30^0={{a\sqrt 3 } \over 2}\Rightarrow AC = 2AI = a\sqrt 3 $

Xét tam giác vuông $SAC$ có: $SA=\sqrt {A{C^2} + S{C^2}} = \sqrt {3{a^2} + {{6{a^2}} \over 4}} =\frac{3a}{\sqrt{2}}.$

Hai tam giác vuông $SCA$ và $IKA$ có:

$\widehat{A} chung$, $\widehat{C}=\widehat{K}=90^0$

⇒ $\Delta SCA \sim \Delta IKA (g-g)$

⇒ $\frac{IK}{SC}=\frac{AI}{AS}\Rightarrow IK=\frac{AI.SC}{AS}=\frac{a}{2}.$

c) $IK = IB = ID = \frac{a}{2}$ nên tam giác $BKD$ vuông tại $K$. (tam giác có trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền thì tam giác đó vuông)

Vậy $\widehat{BKD}=90^{0}.$

Ta có: $SA$ vuông góc với $BD$ (do $BD\perp (SAC)-cmt$) và $SA \perp IK (gt)$ nên $SA ⊥ (DKB)$ ⇒ $SA \perp DK$.

Vì: $DK$ và $BK$ cùng vuông góc với $SA$.

Vậy góc $\widehat {BKD}$ là góc giữa $(SAD)$ và $(SAB)$ và $\widehat{BKD}=90^{0}$ $\Rightarrow (SAD) ⊥ (SAB)$.

Bài trước:

Giải bài 1 2 3 4 5 6 7 8 trang 104 105 sgk Hình học 11

Bài tiếp theo:

Giải bài 1 2 3 4 5 6 7 8 trang 119 120 sgk Hình học 11

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 11 với giải bài 1 2 3 4 5 6 7 8 9 10 11 trang 113 114 sgk Hình học 11!

“Bài tập nào khó đã có giaibaisgk.com“