Nội Dung
Hướng dẫn giải Bài §1. Hình trụ – Diện tích xung quanh và thể tích hình trụ, Chương IV – Hình trụ – Hình nón – Hình cầu, sách giáo khoa toán 9 tập hai. Nội dung bài giải bài 1 2 3 4 5 6 7 trang 110 111 sgk toán 9 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 9.
Lý thuyết
1. Hình trụ
Khi quay vòng quanh một cạnh cố định bất kì, ta được một hình trụ.
2. Cắt hình trụ bởi một mặt phẳng
Mặt cắt là một mặt phẳng song song với đáy ta được một hình tròn bằng hình tròn đáy.
Mặt cắt là một mặt phẳng song song với trục ta được một hình chữ nhật.
3. Diện tích xung quanh hình trụ
Với bán kính đáy $r$ và chiều cao $h$, ta có:
Diện tích xung quanh: \(S_{xq}=2\pi rh\)
Diện tích toàn phần: \(S_{tp}=2\pi rh+2\pi r^2\)
4. Thể tích hình trụ
Thể tích hình trụ được cho bởi công thức: \(V=Sh=\pi r^2h\)
Dưới đây là phần Hướng dẫn trả lời các câu hỏi có trong bài học cho các bạn tham khảo. Các bạn hãy đọc kỹ câu hỏi trước khi trả lời nhé!
Câu hỏi
1. Trả lời câu hỏi 1 trang 107 sgk Toán 9 tập 2
Lọ gốm ở hình 74 có dạng một hình trụ. Quan sát hình và cho biết đâu là đáy, đâu là mặt xung quanh, đâu là đường sinh của hình trụ đó ?

Trả lời:
Đáy gồm $2$ hình tròn ở trên và dưới của lọ gốm.
Mặt xung quanh là mặt bên ngoài của lọ gốm.
Đường sinh là đường thẳng nằm ở mặt xung quanh, nối $2$ đáy của lọ gốm và vuông góc với đáy.
2. Trả lời câu hỏi 2 trang 108 sgk Toán 9 tập 2
Chiếc cốc thủy tinh và ống nghiệm đều có dạng hình trụ (h.76), phải chăng mặt nước trong cốc và mặt nước trong ống nghiệm là những hình tròn ?

Trả lời:
Mặt nước trong cốc và mặt nước trong ống nghiệm là những hình tròn.
3. Trả lời câu hỏi 3 trang 109 sgk Toán 9 tập 2
Quan sát hình $77$ và điền số thích hợp vào các chỗ trống:
– Chiều dài của hình chữ nhật bằng chu vi của đáy hình trụ và bằng: (….)(cm).
– Diện tích hình chữ nhật
(….) . (….) = (….) (cm2).
– Diện tích một đáy của hình trụ
(….) . 5 . 5 = (….) (cm2).
– Tổng diện tích hình chữ nhật và diện tích hai hình tròn đáy (diện tích toàn phần) của hình trụ
(….) + (….) . 2 = (….) (cm2).
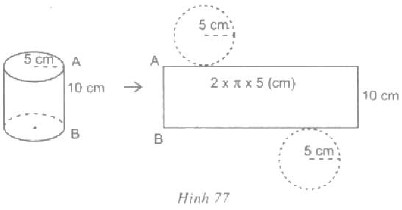
Trả lời:
– Chiều dài của hình chữ nhật bằng chu vi của đáy hình trụ và bằng: \(10\pi \) (cm).
– Diện tích hình chữ nhật : \(10.10\pi = 100\pi \,\,\left( {c{m^2}} \right)\)
– Diện tích một đáy của hình trụ: \(\pi .5.5 = 25\pi \,\,\left( {c{m^2}} \right)\)
– Tổng diện tích hình chữ nhật và diện tích hai hình tròn đáy (diện tích toàn phần) của hình trụ:
\(100\pi + 25\pi .2 = 150\pi \,\,\left( {c{m^2}} \right)\)
Dưới đây là Hướng dẫn giải bài 1 2 3 4 5 6 7 trang 110 111 sgk toán 9 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 9 kèm bài giải chi tiết bài 1 2 3 4 5 6 7 trang 110 111 sgk toán 9 tập 2 của Bài §1. Hình trụ – Diện tích xung quanh và thể tích hình trụ trong Chương IV – Hình trụ – Hình nón – Hình cầu cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 1 trang 110 sgk Toán 9 tập 2
Hãy điền thêm các tên gọi vào dấu “…”

Bài giải:
Điền vào như sau:

(1) Bán kính đáy của hình trụ.
(2) Đáy của hình trụ.
(3) Đường cao của hình trụ.
(4) Đáy của hình trụ.
(5) Đường kính đáy của hình trụ.
(6) Mặt xung quanh của hình trụ.
2. Giải bài 2 trang 110 sgk Toán 9 tập 2
Lấy một băng giấy hình chữ nhật \(ABCD\) (h80). Biết \(AB = 10cm,\) \(BC = 4 cm\); dán băng giấy như hình vẽ (\(B\) sát với \(A\) và \(C\) sát với \(D,\) không được xoắn).
Có thể dán băng để tạo nên mặt xung quanh của hình trụ được không?

Bài giải:
Có thể dán băng giấy để tạo nên mặt xung quanh của hình trụ. Khi làm theo hướng dẫn ta được một hình trụ còn thiếu hai mặt đáy hình tròn.
Chiều cao của hình trụ là \(BC = 4cm\).
3. Giải bài 3 trang 110 sgk Toán 9 tập 2
Quan sát ba hình dưới đây và chỉ ra chiều cao, bán kính của mỗi hình.

Bài giải:
Gọi \(h\) là chiều cao, \(r\) là bán kính đáy của hình trụ.
Ta có:
– Hình a): \(h = 10cm\) và \(r =8:2= 4cm.\)
– Hình b): \(h = 11cm\) và \(r = 1:2=0,5cm.\)
– Hình c): \(h = 3m\) và \(r =7:2= 3,5m\).
4. Giải bài 4 trang 110 sgk Toán 9 tập 2
Một hình trụ có đáy là \(7 cm\), diện tích xung quanh bằng \(352 cm^2\). Khi đó, chiều cao của hình trụ là:
(A) \(3,2 cm\); (B) \(4,6 cm\); (C) \(1,8 cm\);
(D) \(2,1 cm\); (E) Một kết quả khác.
Bài giải:
Ta có : \({S_{xq}}= 352 cm^2,\) \(r = 7cm.\)
Từ công thức \({S_{xq}}= 2πrh\) suy ra \(h= \dfrac{S_{xq}}{2\pi r}.\)
\( \Rightarrow h= \dfrac{352}{2.3,14.7} \approx 8 (cm).\)
Vậy chọn E.
5. Giải bài 5 trang 111 sgk Toán 9 tập 2
Điền đầy đủ kết quả vào những ô trống của bảng sau:
| Hình | Bán kính đáy \((cm)\) | Chiều cao \((cm)\) | Chu vi đáy \((cm)\) | Diện tích đáy \((cm^2)\) | Diện tích xung quanh \((cm^2)\) | Thể tích \((cm^3)\) |
 |
1 | 10 | ||||
| 5 | 4 | |||||
| 8 | \(4\pi\) |
Bài giải:
♦ Khi \(r = 1cm;h = 10cm\) thì hình trụ có
– Chu vi đáy \(C = 2\pi r = 2\pi \left( {cm} \right)\)
– Diện tích đáy là \(S = \pi {r^2} = \pi {.1^2} = \pi \left( {c{m^2}} \right)\)
– Diện tích xung quanh là \({S_{xq}} = 2\pi rh = 2\pi .1.10 = 20\pi \left( {c{m^2}} \right)\)
– Thể tích là \(V = \pi {r^2}h = \pi {.1^2}.10 = 10\pi \left( {c{m^3}} \right)\)
♦ Khi \(r = 5cm;h = 4cm\) thì hình trụ có
– Chu vi đáy \(C = 2\pi r = 2\pi .5 = 10\pi \left( {cm} \right)\)
– Diện tích đáy là \(S = \pi {r^2} = \pi {.5^2} = 25\pi \left( {c{m^2}} \right)\)
– Diện tích xung quanh là \({S_{xq}} = 2\pi rh = 2\pi .5.4 = 40\pi \left( {c{m^2}} \right)\)
– Thể tích là \(V = \pi {r^2}h = \pi {.5^2}.4 = 100\pi \left( {c{m^3}} \right)\)
♦ Khi \(h = 8cm\) và chi vi đáy \(C = 4\pi \) thì hình trụ có
– Bán kính đáy \(r = \dfrac{C}{{2\pi }} = \dfrac{{4\pi }}{{2\pi }} = 2\left( {cm} \right)\)
– Diện tích đáy là \(S = \pi {r^2} = \pi {.2^2} = 4\pi \left( {c{m^2}} \right)\)
– Diện tích xung quanh là \({S_{xq}} = 2\pi rh = 2\pi .2.8 = 32\pi \left( {c{m^2}} \right)\)
– Thể tích là \(V = \pi {r^2}h = \pi {.2^2}.8 = 32\pi \left( {c{m^3}} \right)\)
Vậy ta có bảng sau:
| Hình | Bán kính đáy \((cm)\) | Chiều cao \((cm)\) | Chu vi đáy \((cm)\) | Diện tích đáy \((cm^2)\) | Diện tích xung quanh \((cm^2)\) | Thể tích \((cm^3)\) |
 |
1 | 10 | \(2\pi\) | \(\pi\) | \(20\pi\) | \(10\pi\) |
| 5 | 4 | \(10\pi\) | \(25\pi\) | \(40\pi\) | \(100\pi\) | |
| 2 | 8 | \(4\pi\) | \(4\pi\) | \(32\pi\) | \(32\pi\) |
6. Giải bài 6 trang 111 sgk Toán 9 tập 2
Chiều cao của một hình trụ bằng bán kính đường tròn đáy. Diện tích xung quanh của hình trụ là \(314\) \(c{m^2}.\)
Hãy tính bán kính đường tròn đáy và thể tích hình trụ (làm tròn kết quả đến số thập phân thứ hai).
Bài giải:
Gọi hình trụ có chiều cao là \(h,\) bán kính đáy là \(r.\)
Ta có \({S_{xq}}= 2πrh = 314 \, cm^2.\)
Vì \(h=r\) nên ta có: \(2 \pi r^2=324\) \(\Rightarrow r^2=\dfrac{S_{xq}}{2\pi }.\)
\(\Rightarrow r ≈ 7,07\)
Thể tích của hình trụ:
\( V = πr^2h = 3,14. 7,07^3≈ 1109,65 \, (cm^3).\)
7. Giải bài 7 trang 111 sgk Toán 9 tập 2
Một bóng đèn huỳnh quang dài \(1,2m\). đường kính của đường tròn đáy là \(4cm\), được đặt khít vào một ống giấy cứng dạng hình hộp (h82). Tính diện tích phần cứng dùng để làm hộp.
(Hộp mở hai đầu, không tính lề và mép dán).

Bài giải:
Diện tích phần giấy cứng cần tính chính là diện tích xung quanh của một hộp chữ nhật có đáy là hình vuông cạnh \(4cm\), chiều cao là \(1,2m =120 cm.\)
Diện tích xung quanh của hình hộp:
\({S_{xq}} = 4.4.120 = 1920\,\left( {c{m^2}} \right).\)
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 9 khác
- Để học tốt môn Vật lí lớp 9
- Để học tốt môn Sinh học lớp 9
- Để học tốt môn Ngữ văn lớp 9
- Để học tốt môn Lịch sử lớp 9
- Để học tốt môn Địa lí lớp 9
- Để học tốt môn Tiếng Anh lớp 9
- Để học tốt môn Tiếng Anh lớp 9 thí điểm
- Để học tốt môn Tin học lớp 9
- Để học tốt môn GDCD lớp 9
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với giải bài 1 2 3 4 5 6 7 trang 110 111 sgk toán 9 tập 2!
“Bài tập nào khó đã có giaibaisgk.com“
