Hướng dẫn Giải bài 154 155 156 157 158 159 160 161 162 163 164 165 166 167 trang 64 65 sgk Toán 6 tập 2

Nội Dung

Hướng dẫn giải bài Ôn tập chương III – Phân số, sách giáo khoa toán 6 tập hai. Nội dung bài Giải bài 154 155 156 157 158 159 160 161 162 163 164 165 166 167 trang 64 65 sgk Toán 6 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần số học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 6.

Lý thuyết

Một số bảng tổng kết chương III

Câu hỏi ôn tập chương III

Dưới đây là Hướng dẫn giải bài ôn tập chương III: giải bài 154 155 156 157 158 159 160 161 trang 64 sgk toán 6 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần số học 6 kèm bài giải chi tiết bài 154 155 156 157 158 159 160 161 162 163 164 165 166 167 trang 64 65 sgk Toán 6 tập 2 của bài ôn tập chương III từ bài §1 Mở rộng khái niệm về phân số đến bài §17 Biểu đồ phần trăm trong chương III – Phân số cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 154 155 156 157 158 159 160 161 trang 64 sgk toán 6 tập 2

1. Giải bài 154 trang 64 sgk Toán 6 tập 2

Cho phân số ${x \over 3}$ . Với giá trị nguyên nào của x thì ta có:

a) ${x \over 3} < 0$ b) ${x \over 3} = 0$

c) $0 < {x \over 3} < 1$ d) ${x \over 3} = 1$

e) $1 < {x \over 3} \le 2$

Bài giải:

a) ${x \over 3} < 0 \Rightarrow x < 0$

b) ${x \over 3} = 0 \Rightarrow x = 0$

c) $0 < {x \over 3} < 1 \Rightarrow 0 < x < 3 \Rightarrow x = 1;2$

d) ${x \over 3} = 1 \Rightarrow x = 3$

e) $1 < {x \over 3} \le 2 \Rightarrow 3 < x \le 6 \Rightarrow x = 4;5;6$

2. Giải bài 155 trang 64 sgk Toán 6 tập 2

Điền số thích hợp vào ô vuông:

${{ – 12} \over {16}} = {{ – 6} \over \ldots } = { \ldots \over { – 12}} = {{21} \over \ldots }$

Bài giải:

${{ – 12} \over {16}} = {{ – 6} \over 8} = {9 \over { – 12}} = {{21} \over {28}}$

3. Giải bài 156 trang 64 sgk Toán 6 tập 2

Rút gọn:

a) ${{7.25 – 49} \over {7.24 + 21}}$

b) ${{2.\left( { – 13} \right).9.10} \over {\left( { – 3} \right).4.\left( { – 5} \right).26}}$

Bài giải:

a) Phân tích thành các thừa số chung, rồi rút chúng ra ngoài dấu ngoặc, sau đó rút gọn ta có:

${{7.25 – 49} \over {7.24 + 21}} = {{7(25 – 7)} \over {7(24 + 3)}} = {{18} \over {27}} = {2 \over 3}$

b) Phân tích một số thành tích các số, sau đó rút gọn các số giống nhau ở tử và mẫu ta có:

${{2.\left( { – 13} \right).9.10} \over {\left( { – 3} \right).4.\left( { – 5} \right).26}} = {{2( – 13).3.3.2.5} \over {( – 3).2.2( – 5).13.2}} = {{ – 3} \over 2}$

4. Giải bài 157 trang 64 sgk Toán 6 tập 2

Viết các số đo thời gian sau đây với đơn vị là giờ?

15 phút; 45 phút; 78 phút; 150 phút.

(Ví dụ: 6 phút = ${6 \over {60}}h = {1 \over {10}}h = 0,1h)$ .

Bài giải:

a) 15 phút = ${{15} \over {60}}h = {1 \over 4}h = 0,25h$

b) 45 phút = ${{45} \over {60}}h = {3 \over 4}h = 0,75h$

c) 78 phút = ${{78} \over {60}}h = {{13} \over {10}}h = 1,3h$

d) 150 phút = ${{150} \over {60}}h = {5 \over 2}h = 2,5h$

5. Giải bài 158 trang 64 sgk Toán 6 tập 2

So sánh hai phân số :

a) ${3 \over 4}$ và ${{ – 1} \over { – 4}}$

b) ${{15} \over {17}}$ và ${{25} \over {27}}$

Bài giải:

a) ${{ – 1} \over { – 4}} = {1 \over 4} > 0$ nên ${3 \over { – 4}} < 0 < {{ – 1} \over { – 4}}$

Do đó: ${3 \over { – 4}} < {{ – 1} \over { – 4}}$

b) Quy đồng mẫu ta được:

${{15} \over {17}} = {{15.27} \over {17.27}} = {{405} \over {459}}$

${{25} \over {27}} = {{25.17} \over {27.27}} = {{425} \over {459}}$

$ \Rightarrow {{405} \over {459}} < {{425} \over {459}} \Rightarrow {{15} \over {17}} < {{25} \over {27}}$

6. Giải bài 159 trang 64 sgk Toán 6 tập 2

Các phân số sau đây được sắp xếp theo một quy luật. Hãy quy đồng mẫu các phân số để tìm quy luật đó rồi điền tiếp vào chố trống một phân số thích hợp:

a) ${1 \over 6},{1 \over 3},{1 \over 2}, \ldots $

b) ${1 \over 8},{5 \over {24}},{7 \over {24}}, \ldots $

c) ${1 \over 5},{1 \over 4},{3 \over {10}}, \ldots $

d) ${4 \over {15}},{3 \over {10}},{1 \over 3}, \ldots $

Bài giải:

a) ${1 \over 6},{2 \over 6},{3 \over 6},{4 \over 6}$

b) ${3 \over {24}},{5 \over {24}},{7 \over {24}},{9 \over {24}}$

c) ${4 \over {20}},{5 \over {20}},{6 \over {20}},{7 \over {20}}$

d) ${8 \over {30}},{9 \over {30}},{{10} \over {30}},{{11} \over {30}}$

7. Giải bài 160 trang 64 sgk Toán 6 tập 2

Tìm phân số ${a \over b}$ bằng phân số ${{18} \over {27}}$, biết rằng ƯCLN (a,b)= 13.

Bài giải:

Trước hết ta đưa ${{18} \over {27}}$ về phân số tối giảm. Ta có: ${{18} \over {27}} = {2 \over 3}$

Vậy phân số cần tìm là:

${{2.13} \over {3.13}} = {{26} \over {39}}$

8. Giải bài 161 trang 64 sgk Toán 6 tập 2

Tính giá trị của biểu thức:

$A = – 1,6:\left( {1 + {2 \over 3}} \right)$

$B = 1,4.{{15} \over {49}} – \left( {{4 \over 5} + {2 \over 3}} \right):2{1 \over 5}$

Bài giải:

$A = – 1,6:\left( {1 + {2 \over 3}} \right) = {{ – 16} \over {10}}:{5 \over 3} = {{ – 8} \over 5}.{3 \over 5} = {{ – 24} \over {25}}$

$B = 1,4.{{15} \over {49}} – \left( {{4 \over 5} + {2 \over 3}} \right):2{1 \over 5} = {{14} \over {10}}.{{15} \over {49}} – \left( {{{12 + 10} \over {15}}} \right):{{11} \over 5}$

$ = {3 \over 7} – {{22} \over {15}}.{5 \over {11}} = {3 \over 7} – {2 \over 3} = {{9 – 14} \over {21}} = {{ – 5} \over {21}}$

9. Giải bài 162 trang 65 sgk Toán 6 tập 2

Tìm x, biết:

a) $\left( {2,8x – 32} \right):{2 \over 3} = – 90$

b) $\left( {4,5 – 2x} \right).1{4 \over 7} = {{11} \over {14}}$

Bài giải:

a) Từ $\left( {2,8x{\rm{ }}-{\rm{ }}32} \right):{2 \over 3} = – 90$

Suy ra $2,8x{\rm{ }}-{\rm{ }}32{\rm{ }} = – 90.{2 \over 3}$ .

Hay $2,8x – 32 = – 60$

Chuyển vế ta được $2,8x = – 60 + 32$ hay $2,8x = – 28$ .

Vậy $x = -10.$

b) Từ $\left( {4,5 – 2x} \right).1{4 \over 7} = {{11} \over {14}}$

Suy ra $4,5 – 2x = {{11} \over {14}}:1{4 \over 7}$

Hay $4,5 – 2x = {{11} \over {14}}:{{11} \over 7} \Rightarrow 4,5 – 2x = {{11} \over {14}}.{7 \over {11}}$

Do đó $4,5 – 2x = 0,5$. Chuyển vế ta được: $2x = 4,5 – 0,5$ hay $2x = 4$

Vậy $x = 2$

10. Giải bài 163 trang 65 sgk Toán 6 tập 2

Một cửa hàng bán $356,5m$ vải gồm hai loại: vải hoa và vải trăng. Biết số vài hoa bằng 78,25% số vài trắng. Tính số mét vải mỗi loại.

Bài giải:

Số vải hoa bằng 78,25% số vải trắng.

Toàn bộ số vải của cửa hàng bằng số vải hoa cộng số vải trắng.

Do đó toàn bộ số vải bằng:

78,25% số vải trắng + 100% số vải trắng = 178,25% số vải trắng.

Theo đầu bài tổng số vải này là 356,5m, nghĩa là 178,25% số vải trắng bằng 356,5m.

Suy ra số vải trắng là:

$356,5:178,25\% = {{356,5.100} \over {178,25}} = 200\left( m \right)$

Số vải hoa là:

$356,5 – 200 = 156,5 (m)$

Vậy số vải trắng là: $200m.$

Số vải hoa là : $156,5 m.$

11. Giải bài 164 trang 65 sgk Toán 6 tập 2

Khi trả tiền mua một cuốn sách theo đúng giá bìa, Oanh được cửa hàng trả lại $1200$ đồng vì đã được khuyến mại 10%. Vậy Oanh đã mua cuốn sách với giá bao nhiêu?

Bài giải:

Bạn Oanh được trả lại $1200$ đồng vì khuyến mại 10%

Điều đó có nghĩa là 10% của giá cuốn sách bằng $1200đ.$

Do đó giá cuốn sách bằng:

$1200:10\% = 1200:{{10} \over {100}} = 12000$ đồng

12. Giải bài 165 trang 65 sgk Toán 6 tập 2

Một người gửi tiết kiệm 2 triệu đồng, tính ra mỗi tháng được lãi $11200$ đồng. Hỏi người ấy đã gửi tiết kiệm với lãi suất bao nhiêu phần trăm một tháng?

Bài giải:

Ta có: Lãi suất = Số tiền lãi / Tiền vốn

Vậy số lãi suất 1 tháng là:

${{11200} \over {2000000}} = 0,56\% $

13. Giải bài 166 trang 65 sgk Toán 6 tập 2

Học kì $I$, số học sinh giỏi của lớp $6D$ bằng ${2 \over 7}$ số học sinh còn lại. Sang học kì $II$, số học sinh giỏi tăng thêm $8$ bạn (số học sinh cả lớp không đổi), nên số học sinh giỏi bằng ${2 \over 3}$ số còn lại. Hỏi học kì $I$ lớp $6D$ có bao nhiêu học sinh giỏi?

Bài giải:

Ta có thể giải bài trên bằng 2 cách:

♦ Cách 1:

Theo đầu bài số học sinh bằng ${2 \over 7}$ số học sinh còn lại nghĩa là số học sinh còn lại chia thành 7 phần thì số học sinh giỏi chiếm 2 phần.

Do đó số học sinh của cả lớp chiếm $9$ phần.

Vì thế số học sinh giỏi kì I bằng ${2 \over 9}$ số học sinh của cả lớp.

Tương tự, số học sinh giỏi học kì II bằng ${2 \over 5}$ số học sinh của cả lớp.

Theo đầu bài, số học sinh giỏi học kì II trừ đi số học sinh giỏi học kì I bằng 8; nghĩa là ${2 \over 5}$ số học sinh của cả lớp trừ đi ${2 \over 9}$ số học sinh của cả lớp bằng 8 hay $\left( {{2 \over 5} – {2 \over 9}} \right)$ số học sinh của cả lớp bằng 8 hay ${8 \over {45}}$ số học sinh của cả lớp bằng 8.

Suy ra số học sinh của cả lớp bằng 8 :${8 \over {45}}$ = $45$ (học sinh)

Vậy số học sinh giỏi học kì I bằng ${2 \over 9}$.45 = $10$ (học sinh).

♦ Cách 2:

Có thể đưa về bài toán tìm $x$ như sau:

Gọi $x$ là số học sinh giỏi học kì $I$.

Theo đầu bài, ${2 \over 7}$ số học sinh còn lại bằng x nên số học sinh còn lại là:

$x:{2 \over 7} = {{7x} \over 2}$

Ta có số học sinh giỏi học kì II là: $x + 8$ và số học sinh còn lại là: ${{7x} \over 2} – 8$

Theo đầu bài, số học sinh giỏi học kì II bằng ${2 \over 3}$ số học sinh còn lại, nghĩa là:

$x + 8 = {2 \over 3}\left( {{{7x} \over 2} – 8} \right)$ hay $x + 8 = {{7x} \over 3} – {{16} \over 3}$

Chuyển vế ta được: ${{7x} \over 3} – x = 8 + {{16} \over 3}$ hay $7x – 3x = 24 + 16.$

Suy ra $4x = 40$. Vậy $x = 10.$

14. Giải bài 167 trang 65 sgk Toán 6 tập 2

Đố: Đố em lập được một đề toán mà khi dung máy tính bỏ túi người giải đã bấm liên tiếp như sau:

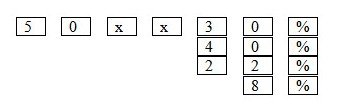
Bài giải:

Một lớp có $50$ học sinh. Cuối học kì $I$ lớp có 30% học sinh giỏi, 40% học sinh khá, 22% học sinh trung bình và 8% học sinh yếu kém. Hãy tính số học sinh mỗi loại.

Bài trước:

Trả lời câu hỏi ôn tập 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 trang 62 sgk Toán 6 tập 2

Bài tiếp theo:

Trả lời câu hỏi ôn tập cuối năm 1 2 3 4 5 6 7 8 9 trang 65 66 sgk Toán 6 tập 2

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 6 với Giải bài 154 155 156 157 158 159 160 161 162 163 164 165 166 167 trang 64 65 sgk Toán 6 tập 2!

“Bài tập nào khó đã có giaibaisgk.com“