Toán lớp 9

Giải bài 26 27 trang 88 sgk Toán 9 tập 1

Hướng dẫn giải Bài §4. Một số hệ thức về cạnh và góc trong tam giác vuông, chương I – Hệ thức lượng trong tam giác vuông, sách giáo khoa toán 9 tập một. Nội dung bài giải bài 26 27 trang 88 sgk toán 9 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 9.

Lý thuyết

1. Các hệ thức

Giải bài 26 27 trang 88 sgk toán 9 tập 1

ĐỊNH LÍ:

Trong tam giác vuông mỗi cạnh góc vuông bằng:

a) Cạnh huyền nhân với sin góc đối hoặc nhân với cos góc kề

b) Cạnh góc vuông kia nhân với tan góc đối hoặc nhân với cotan góc kề

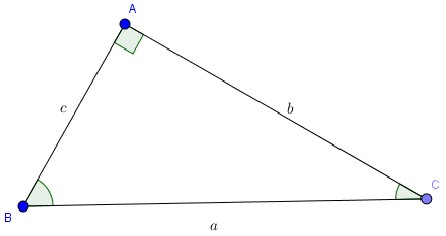
Cụ thể trong tam giác trên thì:

\(b=a.sinB=a.cosC;c=a.sinC=a.cosB\)

\(b=c.tanB=c.cotC;c=b.tanC=b.cotB\)

2. Áp dụng giải tam giác vuông

Cho tam giác ABC vuông tại A có BC=10 và \(\widehat{C}=30^{\circ}\). Giải tam giác vuông ABC.

Bài giải:

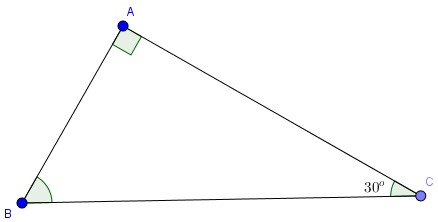
Ta dễ dàng suy ra: \(\widehat{B}=60^{\circ}\)

\(AC=BC.cosC=10.cos30^{\circ}=10.\frac{\sqrt{3}}{2}=5.\sqrt{3}\)

\(AB=BC.sinC=10.sin30^{\circ}=10.\frac{1}{2}=5\)

Dưới đây là phần Hướng dẫn trả lời các câu hỏi có trong bài học cho các bạn tham khảo. Các bạn hãy đọc kỹ câu hỏi trước khi trả lời nhé!

Câu hỏi

1. Trả lời câu hỏi 1 trang 85 sgk Toán 9 tập 1

Viết các tỉ số lượng giác của góc $B$ và góc $C$. Từ đó hãy tính mỗi cạnh góc vuông theo:

a) Cạnh huyền và các tỉ số lượng giác của góc $B$ và góc $C$;

b) Cạnh góc vuông còn lại và các tỉ số lượng giác của góc $B$ và góc $C$.

Trả lời:

Ta có:

\(\eqalign{& \sin B = {b \over a};\,\,\cos B = {c \over a};\,\,tgB = {b \over c};\,\,{\mathop{\rm cotgB}\nolimits} = {c \over b} \cr & \sin C = {c \over a};\,\,\cos C = {b \over a};\,\,tgC = {c \over b};\,\,{\mathop{\rm cotgB}\nolimits} = {b \over c} \cr} \)

a) Ta có:

\(\eqalign{& b = a.\left( {{b \over a}} \right) = a.\sin B = a.\cos C \cr & c = a.\left( {{c \over a}} \right) = a.\cos B = a.\sin C \cr} \)

b) Ta có:

\(\eqalign{& b = c.\left( {{b \over c}} \right) = c.tgB = c.{\mathop{\rm cotg}\nolimits} C \cr & c = b.\left( {{c \over b}} \right) = b.{\mathop{\rm cotg}\nolimits} B = b.tgC \cr} \)

2. Trả lời câu hỏi 2 trang 87 sgk Toán 9 tập 1

Trong ví dụ 3, hãy tính cạnh $BC$ mà không áp dụng định lý Py-ta-go.

Trả lời:

Ta có:

\(\eqalign{& tgB = {{AC} \over {AB}} = {8 \over 5} \cr & \Rightarrow B \approx {58^o} \cr & \Rightarrow \sin B = {{AC} \over {BC}} \approx 0,848 \cr & \Rightarrow BC = {{AC} \over {0,848}} \approx 9,433 \cr} \)

3. Trả lời câu hỏi 3 trang 87 sgk Toán 9 tập 1

Trong ví dụ 4, hãy tính các cạnh \(OP;OQ\) qua côsin của các góc \(P\) và \(Q.\)

Trả lời:

Ta có \(\widehat Q = 90^\circ – \widehat P = 90^\circ – 36^\circ = 54^\circ .\)

Theo các hệ thức giữa cạnh và góc trong tam giác vuông, ta có:

\(OP = PQ.\cos \,P = 7.\cos 36^\circ \approx 5,663\)

\(OQ = PQ.\cos \,Q = 7.\cos 54^\circ \approx 4,114.\)

Dưới đây là Hướng dẫn giải bài 26 27 trang 88 sgk toán 9 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 9 kèm bài giải chi tiết bài 26 27 trang 88 sgk toán 9 tập 1 của bài §4. Một số hệ thức về cạnh và góc trong tam giác vuông trong chương I – Hệ thức lượng trong tam giác vuông cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 26 trang 88 sgk Toán 9 tập 1

Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng $34^0$ và bóng của một tháp trên mặt đất dài $86m$ (h.30). Tính chiều cao của tháp (làm tròn đến mét).

Bài giải:

Đặt tên các điểm như hình vẽ:

Xét tam giác \(ABC\) vuông tại \(A\). Ta có:

\(\tan B = \dfrac{AC}{AB} \Leftrightarrow \tan 34^o = \dfrac{AC}{86}\)

\(\Leftrightarrow AC = 86. \tan 34^o \approx 58 (m)\)

Vậy chiều cao của tháp là: \(\approx 58 (m)\).

2. Giải bài 27 trang 88 sgk Toán 9 tập 1

Giải tam giác ABC vuông tại A, biết rằng:

a) $b = 10cm, \widehat{C} = 30^0$

b) $c = 10cm, \widehat{C} = 45^0$

c) $a = 20cm, \widehat{B} = 35^0$

d) $c = 21cm, b = 18cm$

Bài giải:

a)  Ta có:

$\widehat{B}$ = $90^0$ – $30^0$ = $60^0$

Áp dụng hệ thức về cạnh và góc trong tam giác vuông $ABC$, ta có:

$AB = AC.tg C$

$ = 10.tg 30^0 = 10.\frac{\sqrt{3}}{3} \approx 5,774 (cm)$

$AC = BC.cos C$

$⇒ BC = \frac{AC}{cos C} = \frac{10}{\frac{\sqrt{3}}{2}} \approx 11,547 (cm)$

b) Ta có:

$\widehat{B}$ = $90^0$ – $45^0$ = $45^0$ nên $ABC$ là tam giác vuông cân tại $A$.

Do đó: $AB = AC = 10 (cm)$

Áp dụng hệ thức về cạnh và góc trong tam giác vuông $ABC$, ta có:

$AB = BC. sin C$

$⇒ BC = \frac{AB}{sin C} = \frac{10}{sin 45^0} \approx 14,142 (cm)$

c) Ta có:

$\widehat{C}$ = $90^0$ – $35^0$ = $55^0$

Áp dụng hệ thức về cạnh và góc trong tam giác vuông ABC, ta có:

$AB = BC.cos B = 20.cos 35^0 \approx 16,383 (cm)$

$AC = BC.sin B = 20.sin 35^0 \approx 11,472 (cm)$

d) Ta có:

Áp dụng tỉ số lượng giác của góc nhọn, ta có:

$tg B = \frac{AC}{AB} = \frac{18}{21} \approx 0,8571$

$⇒ \widehat{B} \approx 41^0$

$\widehat{C} = 90^0 – \widehat{B} \approx 49^0$

Áp dụng hệ thức về cạnh và góc trong tam giác vuông $ABC$, ta có:

$AB = BC. cos B$

$⇒ BC = \frac{AB}{cos B} = \frac{21}{cos 41^0} \approx 27,825 (cm)$

Bài trước:

Bài tiếp theo:

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với giải bài 26 27 trang 88 sgk toán 9 tập 1!

“Bài tập nào khó đã có giaibaisgk.com“