Luyện tập: Giải bài 20 21 22 23 24 25 trang 84 sgk Toán 9 tập 1

Nội Dung

Luyện tập Bài §3. Bảng lượng giác, chương I – Hệ thức lượng trong tam giác vuông, sách giáo khoa toán 9 tập một. Nội dung bài giải bài 20 21 22 23 24 25 trang 84 sgk toán 9 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 9.

Lý thuyết

1. Cấu tạo của bảng lượng giác

Bảng lượng giác bao gồm bảng VIII, bảng IX, bảng X của cuốn ” bảng số với 4 chữ số thập phân” PDF EPUB PRC AZW miễn phí đọc trên điện thoại – máy tính, ứng dụng đọc file epub, prc reader, azw reader của tác giả V.M. Bra-đi-xơ

Người ta lập bảng dựa trên tính chất:

Nếu hai góc nhọn $\alpha$ và $\beta$ phụ nhau ($\alpha +\beta=90^{\circ}$) thì $sin\alpha =cos\beta ,cos\alpha =sin\beta ,tan\alpha =cot\beta ,cot\alpha =tan\beta$

– Bảng VIII dùng để tính giá trị sin và cos của các góc nhọn đồng thời cũng để tìm góc khi biết sin và cos của góc đó. Có cấu tạo 16 cột và các hàng

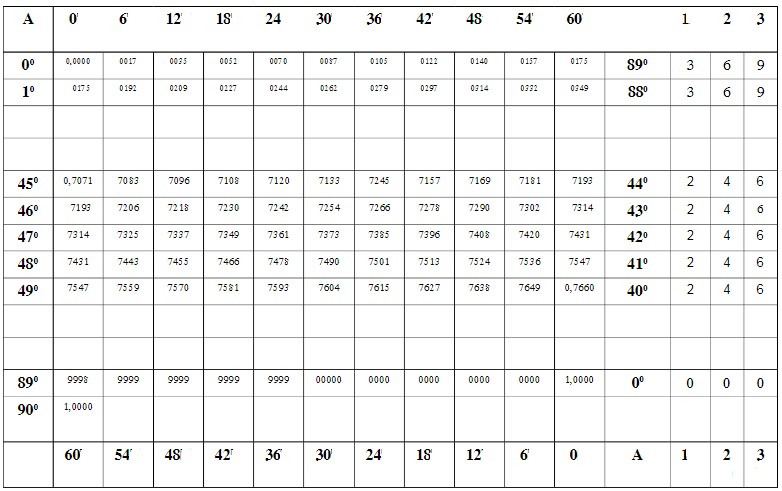
Cột 1 và 13 ghi các số nguyên độ. Cột 1 từ trên xuống ghi số độ tăng dần từ $0^{\circ}$ đến $90^{\circ}$, cột 13 ngược lại giảm dần.

3 cột cuối ghi các giá trị dùng để hiệu chỉnh đối với các góc sai khác 1′ , 2′ , 3′

– Bảng IX dùng để tìm giá trị của tan các góc từ $0^{\circ}$ đến $76^{\circ}$ và cot các góc từ $14^{\circ}$ đến $90^{\circ}$ và ngược lại tìm góc khi biết tan và cot. Cấu tạo tương tự bảng VIII.

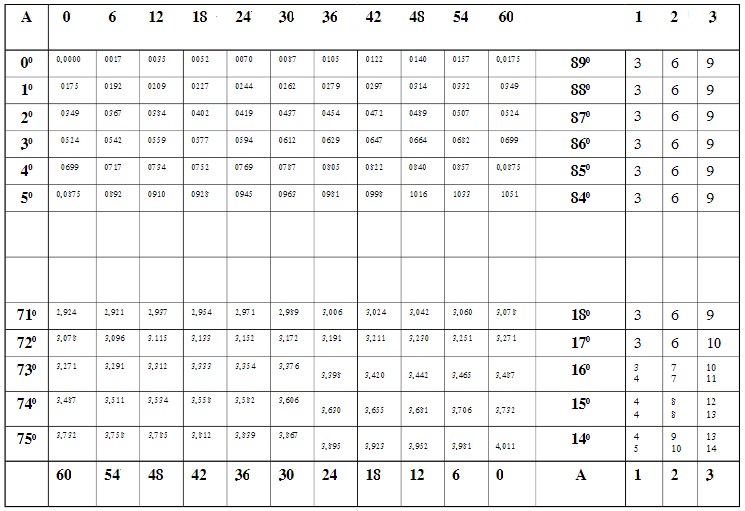
– Bảng X dùng để tìm giá trị của tan các góc $76^{\circ}$ đến $89^{\circ}59{}’$ và cot các góc từ $1{}’$ đến $14^{\circ}$ và ngược lại tìm góc nhọn khi biết tang và cotang.

2. Cách dùng bảng

a) Tìm tỉ số lượng giác của một góc nhọn cho trước

Bước 1: Tra số độ ở cột 1 đối với sin và tang ( cột 13 đối với cos và cotang).

Bước 2: Tra số phút ở hàng 1 đối với sin và tang (hàng cuối đối với cos và cotang).

Bước 3: Lấy giá trị là giao hàng ghi số độ và cột ghi số phút.

b) Tìm số đo của một góc nhọn có tỉ số lượng giác của góc đó

Tra giá trị của tỉ số lượng giác với bảng thích hợp sau đó dóng sang cột độ và hàng phút tương ứng với tỉ số. Ta sẽ có số đo góc cần tìm.

Dưới đây là Hướng dẫn giải bài 20 21 22 23 24 25 trang 84 sgk toán 9 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Luyện tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 9 kèm bài giải chi tiết bài 20 21 22 23 24 25 trang 84 sgk toán 9 tập 1 của bài §3. Bảng lượng giác trong chương I – Hệ thức lượng trong tam giác vuông cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 20 21 22 23 24 25 trang 84 sgk toán 9 tập 1

1. Giải bài 20 trang 84 sgk Toán 9 tập 1

Dùng bảng lượng giác (có sử dụng phần hiệu chỉnh) hoặc máy tính bỏ túi, hãy tìm các tỉ số lượng giác sau (làm tròn đến chữ số thập phân thứ tư):

a) Sin $70^0$13’ ; b) cos $25^0$32’ ;

c) tg $43^0$10’ ; d) cotg $32^0$15’

Bài giải:

a) $Sin 70^013’ \approx 0,9410$

b) $cos 25^032’ \approx 0,9023$

c) $tg 43^010’ \approx 0,9380$

d) $cotg 32^015’ \approx 1,5849$

2. Giải bài 21 trang 84 sgk Toán 9 tập 1

Dùng bảng lượng giác hoặc máy tính bỏ túi để tìm góc nhọn x (làm tròn kết quả đến độ), biết rằng:

a) $sin x = 0,3495 $; b) $cos x = 0,5427$ ;

c) $tg x = 1,5142$; d) $cotg x = 3,163$.

Bài giải:

a) $sin x = 0,3495 ⇒ x \approx 20^0$

b) $cos x = 0,5427 ⇒ x \approx 57^0$

c) $tg x = 1,5142 ⇒ x \approx 57^0$

d) $cotg x = 3,163 ⇒ x \approx 18^0$

3. Giải bài 22 trang 84 sgk Toán 9 tập 1

So sánh

a) sin $20^0$ và sin $70^0$ ; b) cos $25^0$ và cos $63^0$15’

c) tg $73^0$20’ và tg $45^0$ ; d) cotg $2^0$ và cotg $37^0$40’

Bài giải:

Ta có: Khi góc $\alpha$ tăng từ $0^0$ đến $90^0$ thì sin $\alpha$ và tg $\alpha$ tăng còn cos $\alpha$ và cotg $\alpha$ giảm.

a) Vì $20^0 < 70^0$ nên $sin 20^0 < sin 70^0$

b) Vì $25^0 < 63^0$ nên $cos 25^0 > cos 63^015’$

c) Vì $73^0 > 45^0$ nên $tg 73^020’ > tg 45^0$

d) Vì $2^0 < 37^0$ nên $cotg 2^0 > cotg 37^040’$

4. Giải bài 23 trang 84 sgk Toán 9 tập 1

Tính

a) $\frac{sin 25^0}{cos 65^0}$ ;

b) $tg 58^0 – cotg 32^0$.

Bài giải:

a) Vì góc $25^0$ và góc $65^0$ là hai góc phụ nhau nên $cos 65^0 = sin 25^0$. Do đó ta có:

$\frac{sin 25^0}{cos 65^0} = \frac{sin 25^0}{sin 25^0} = 1$

b) Vì góc $58^0$ và góc $32^0$ là hai góc phụ nhau nên $cotg 32^0 = tg 58^0$. Do đó ta có:

$tg 58^0 – cotg 32^0 = tg 58^0 – tg 58^0 = 0$

5. Giải bài 24 trang 84 sgk Toán 9 tập 1

Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần:

a) sin $78^0$, cos $14^0$, sin $47^0$, cos $87^0$.

b) tg $73^0$, cotg $25^0$, tg $62^0$, cotg $38^0$.

Bài giải:

a) Ta có:

$\cos 14^{\circ}=\sin(90^o – 14^o)=\sin 76^{\circ}$;

$\cos 87^{\circ}=\sin (90^o – 87^o)=\sin 3^{\circ}.$.

Vì $ 3^o < 47^o < 76^o < 78^o$

$\Rightarrow \sin 3^{\circ}< \sin 47^{\circ}< \sin 76^{\circ}< \sin 78^{\circ}$

$\Rightarrow \cos 87^{\circ}< \sin 47^{\circ}< \cos 14^{\circ} < \sin 78^o$.

b) Ta có:

$\cot 25^{\circ}=\tan (90^o – 25^o)=\tan 65^{\circ}; $

$\cot 38^{\circ}=\tan (90^o – 38^o)=\tan 52^{\circ}$.

Vì $52^o < 62^o < 65^o < 73^o$

$\Rightarrow \tan 52^{\circ}< \tan 62^{\circ}< \tan 65^{\circ}< \tan 73^{\circ}$;

$\Rightarrow \cot 38^{\circ}< \tan 62^{\circ}< \cot 25^{\circ}< \tan 73^{\circ}$.

6. Giải bài 25 trang 84 sgk Toán 9 tập 1

So sánh

a) tg $25^0$ và sin $25^0$ ; b) cotg $32^0$ và cos $32^0$

c) tg $45^0$ và cos $45^0$ ; d) cotg $60^0$ và sin $30^0$

Bài giải:

♦ Cách 1:

Áp dụng tính chất sin $\alpha$ < tg $\alpha$, cos $\alpha$ < cotg $\alpha$. Ta có:

a) tg $25^0$ > sin $25^0$

b) cotg $32^0$ > cos $32^0$

c) cos $45^0$ = sin $45^0$ mà tg $45^0$ > sin $45^0$ nên tg $45^0$ > cos $45^0$

d) cos $60^0$ = sin $30^0$ mà cotg $60^0$ > cos $60^0$ nên cotg $60^0$ > sin $30^0$

♦ Cách 2:

a) Ta có $\tan 25^o = \dfrac{\sin 25^o}{\cos 25^o}$. Vì $0< \cos 25^o < 1$

$\Rightarrow \dfrac{1}{\cos 25^o} > 1$

$\Leftrightarrow \sin 25^o . \dfrac{1}{\cos 25^o} > \sin 25^o$.

$\Leftrightarrow \dfrac{\sin 25^o}{\cos 25^o} > \sin 25^o$.

$\Leftrightarrow \tan 25^o > \sin 25^o$.

b) Ta có: $\cot 32^o = \dfrac{\cos 32^o}{\sin 32^o}$. Vì $0< \sin 32^o < 1$

$\Rightarrow \dfrac{1}{\sin 32^o} > 1$

$\Leftrightarrow \cos 32^o. \dfrac{1}{\sin 32^o} > 1.\cos 32^o$

$\Leftrightarrow \dfrac{\cos 32^o}{\sin 32^o} > \cos 32^o$

$\Leftrightarrow \cot 32^o > \cos 32^o$.

c) Ta có $\tan 45^o = \dfrac{\sin 45^o}{\cos 45^o}$. Vì $0< \cos 45^o < 1$

$\Rightarrow \dfrac{1}{\cos 45^o} > 1$

$\Leftrightarrow \sin 45^o . \dfrac{1}{\cos 45^o} > \sin 45^o$.

$\Leftrightarrow \dfrac{\sin 45^o}{\cos 45^o} > \sin 45^o$.

$\Leftrightarrow \tan 45^o > \sin 45^o$

Mà $\sin 45^o= \cos(90^o – 45^o)=\cos 45^o$

Vậy $ \tan 45^o > \cos 45^o$.

d) Ta có: $\cot 60^o = \dfrac{\cos 60^o}{\sin 60^o}$. Vì $0< \sin 60^o < 1$

$\Rightarrow \dfrac{1}{\sin 60^o} > 1$

$\Leftrightarrow \cos 60^o. \dfrac{1}{\sin 60^o} > 1.\cos 60^o$

$\Leftrightarrow \dfrac{\cos 60^o}{\sin 60^o} > \cos 60^o$

$\Leftrightarrow \cot 60^o > \cos 60^o $.

Mà $\cos 60^o = sin (90^o -60^o) = \sin 30^o$

Do đó $ \cot 60^o > \sin 30^o$.

Bài trước:

Giải bài 18 19 trang 83 84 sgk Toán 9 tập 1

Bài tiếp theo:

Giải bài 26 27 trang 88 sgk Toán 9 tập 1

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với giải bài 20 21 22 23 24 25 trang 84 sgk toán 9 tập 1!

“Bài tập nào khó đã có giaibaisgk.com“