Nội Dung
Luyện tập Bài §4. Một số hệ thức về cạnh và góc trong tam giác vuông, chương I – Hệ thức lượng trong tam giác vuông, sách giáo khoa toán 9 tập một. Nội dung bài giải bài 28 29 30 31 32 trang 89 sgk toán 9 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 9.
Lý thuyết
1. Các hệ thức
ĐỊNH LÍ:
Trong tam giác vuông mỗi cạnh góc vuông bằng:
a) Cạnh huyền nhân với sin góc đối hoặc nhân với cos góc kề
b) Cạnh góc vuông kia nhân với tan góc đối hoặc nhân với cotan góc kề
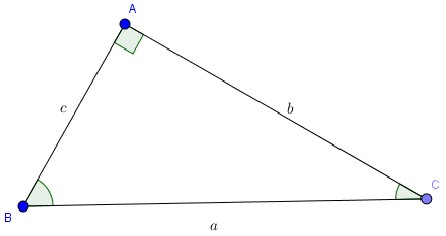
Cụ thể trong tam giác trên thì:
\(b=a.sinB=a.cosC;c=a.sinC=a.cosB\)
\(b=c.tanB=c.cotC;c=b.tanC=b.cotB\)
2. Áp dụng giải tam giác vuông
Cho tam giác ABC vuông tại A có BC=10 và \(\widehat{C}=30^{\circ}\). Giải tam giác vuông ABC.
Bài giải:
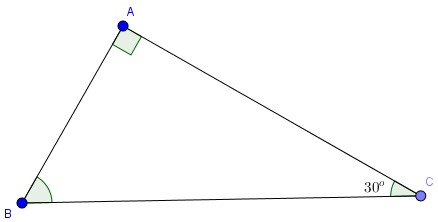
Ta dễ dàng suy ra: \(\widehat{B}=60^{\circ}\)
\(AC=BC.cosC=10.cos30^{\circ}=10.\frac{\sqrt{3}}{2}=5.\sqrt{3}\)
\(AB=BC.sinC=10.sin30^{\circ}=10.\frac{1}{2}=5\)
Dưới đây là Hướng dẫn giải bài 28 29 30 31 32 trang 89 sgk toán 9 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Luyện tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 9 kèm bài giải chi tiết bài 28 29 30 31 32 trang 89 sgk toán 9 tập 1 của bài §4. Một số hệ thức về cạnh và góc trong tam giác vuông trong chương I – Hệ thức lượng trong tam giác vuông cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 28 trang 89 sgk Toán 9 tập 1
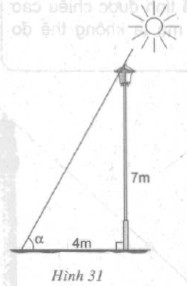
Một cột đèn cao $7m$ có bóng trên mặt đất dài $4m$. Hãy tính góc (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất (góc $\alpha$ trong hình 31).
Bài giải:
Ta có:
$tg \alpha = \frac{7}{4} ⇒ \alpha \approx 60^015′$
2. Giải bài 29 trang 89 sgk Toán 9 tập 1
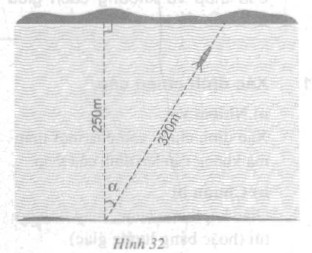
Một khúc sông rộng khoảng $250m$. Một chiếc đò chèo qua sông bị dòng nước đẩy xiên nên phải chèo khoảng $320m$ mới sang được bờ bên kia. Hỏi dòng nước đã đẩy chiếc đò lệch đi một góc bằng bao nhiêu độ? (góc $\alpha$ trong hình 32).
Bài giải:
Ta có:
$cos \alpha = \frac{250}{320}⇒ \alpha \approx 38^037′$
Vậy dòng nước đã đẩy chiếc đò lệch đi một góc $\alpha \approx 38^037′$
3. Giải bài 30 trang 89 sgk Toán 9 tập 1
Cho tam giác $ABC$, trong đó $BC = 11cm, \widehat{ABC} = 38^0, \widehat{ACB} = 30^0$. Gọi điểm $N$ là chân đường vuông góc kẻ từ $A$ đến cạnh $BC$. Hãy tính:
a) Đoạn thẳng $AN$.
b) Cạnh $AC$.
Gợi ý: kẻ $BK$ vuông góc với $AC.$
Bài giải:
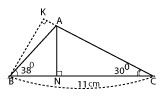
a) Kẻ $BK \perp AC$
Ta có:
$\widehat{KBC} = 90^0 – 30^0 = 60^0$,
$\widehat{KBA} = 60^0 – 38^0 = 22^0$
Áp dụng hệ thức về cạnh và góc trong tam giác $KBC$ vuông tại $K$, ta có:
$BK = BC.sin C = 11.sin 30^0 \approx 5,5 (cm)$
Áp dụng hệ thức về cạnh và góc trong tam giác $KBA$ vuông tại $K$, ta có:
$BK = AB.cos \widehat{KBA}$
$⇒ AB = \frac{BK}{cos \widehat{KBA}}$
$ = \frac{5,5}{cos 22^0} \approx 5,932 (cm)$
Áp dụng hệ thức về cạnh và góc trong tam giác $ABN$ vuông tại $N$, ta có:
$AN = AB.sin \widehat{ABN} $
$= 5,932. sin 38^0 \approx 3,652 (cm)$
b) Áp dụng hệ thức về cạnh và góc trong tam giác $ACN$ vuông tại $N$, ta có:
$AN = AC.sin C$
$ ⇒ AC = \frac{AN}{sin C} $
$= \frac{3,652}{sin 30^0} \approx 7,304 (cm)$
4. Giải bài 31 trang 89 sgk Toán 9 tập 1
Trong hình 33, $AC = 8cm, AD = 9,6cm, \widehat{ABC} = 90^0, \widehat{ACB} = 54^0$ và $\widehat{ACD} = 74^0$. Hãy tính:
a) $AB$.
b) $\widehat{ADC}$
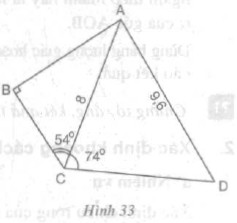
Bài giải:
a) Áp dụng hệ thức về cạnh và góc trong tam giác $ABC$ vuông tại $B$, ta có:
$AB = AC.\widehat{ACB} = AC.sin 54^0 = 8.0,809 \approx 6,472 (cm)$
b) Kẻ đường cao $AH$ của tam giác $ACD$.
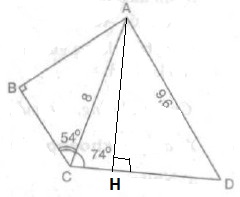
Áp dụng hệ thức về cạnh và góc trong tam giác AHC vuông tại H, ta có:
$AH = AC.sin \widehat{ACH} $
$= 8.sin 74^0 \approx 7,690 (cm)$
Áp dụng hệ thức về cạnh và góc trong tam giác $AHD$ vuông tại $H$, ta có:
$AH = AD.sin D$
$⇒ sin D = \frac{AH}{AD} \approx \frac{7,69}{9,6} \approx 0,801$
Suy ra $\widehat{D} \approx 53^0$.
5. Giải bài 32 trang 89 sgk Toán 9 tập 1
Một con thuyền với vận tốc $2km/h$ vượt qua một khúc sông nước chảy mạnh mất 5 phút. Biết rằng đường đi của con thuyền tạo với bờ một góc $70^0$. Từ đó đã có thể tính được chiều rộng của khúc sông chưa? Nếu có thể hãy tính kết quả (làm tròn đến mét).
Bài giải:
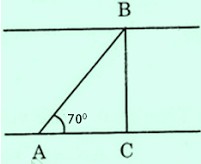
Gọi \(AB\) là đoạn đường mà con thuyền đi được trong \(5\) phút, \(BC\) là chiều rộng của khúc sông.
Đổi \(5\) phút \(=\dfrac{1}{12}h.\) Biết vận tốc của thuyền là \(v=2km/h\)
Suy ra quãng đường thuyền đi trong \(5\) phút là: \(AB=S=v.t=2.\dfrac{1}{12}=\dfrac{1}{6}.\)
Xét tam giác \(CAB\) vuông tại \(C\), \(AB=\dfrac{1}{6},\ \widehat{A}=70^o\), ta có:
\(BC=AB. \sin A = \dfrac{1}{6}. \sin 70^o \approx 0,1566(km).\)
Vậy chiều rộng khúc sông xấp xỉ \(157(m)\).
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 9 khác
- Để học tốt môn Vật lí lớp 9
- Để học tốt môn Sinh học lớp 9
- Để học tốt môn Ngữ văn lớp 9
- Để học tốt môn Lịch sử lớp 9
- Để học tốt môn Địa lí lớp 9
- Để học tốt môn Tiếng Anh lớp 9
- Để học tốt môn Tiếng Anh lớp 9 thí điểm
- Để học tốt môn Tin học lớp 9
- Để học tốt môn GDCD lớp 9
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với giải bài 28 29 30 31 32 trang 89 sgk toán 9 tập 1!
“Bài tập nào khó đã có giaibaisgk.com“