Hướng dẫn Giải bài 27 28 trang 58 sgk Toán 9 tập 1

Nội Dung

Hướng dẫn giải Bài §5. Hệ số góc của đường thẳng $y = ax + b (a ≠ 0)$, chương II – Hàm số bậc nhất, sách giáo khoa toán 9 tập một. Nội dung bài giải bài 27 28 trang 58 sgk toán 9 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần đại số có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 9.

Lý thuyết

1. Khái niệm hệ số góc của đường thẳng $y = ax + b (a ≠ 0)$.

Xét đường thẳng $y=ax+b (a \neq 0)$. Khi đó a được gọi là hệ số góc của đường thẳng $y=ax+b$

2. Tính chất

Gọi A là giao điểm của đường thẳng $y=ax+b$ và trục Ox, T là điểm thuộc đường thẳng $y=ax+b$ và có tung độ dương. Ta gọi góc tạo bởi đường thẳng $y=ax+b$ và trục Ox là góc tạo bởi tia AT và tia Ax. Đặt góc đó là $\alpha$

Nếu $a>0$ thì $0^{\circ}<\alpha<90^{\circ}$ và $\tan \alpha =a$

Nếu $a<0$ thì $0^{\circ}<\alpha<180^{\circ}$ và $\tan (180^{\circ}-\alpha) =-a$

Dưới đây là phần Hướng dẫn trả lời các câu hỏi có trong bài học cho các bạn tham khảo. Các bạn hãy đọc kỹ câu hỏi trước khi trả lời nhé!

Câu hỏi

Trả lời câu hỏi trang 56 sgk Toán 9 tập 1

Hình 11a) biểu diễn đồ thị của các hàm số (với hệ số $a > 0$)

$y = 0,5x + 2;$ $y = x + 2;$ $y = 2x + 2.$

Hình 11b) biểu diễn đồ thị của các hàm số (với hệ số $a < 0$):

$y = -2x + 2;$ $y = -x + 2;$ $y = -0,5x + 2.$

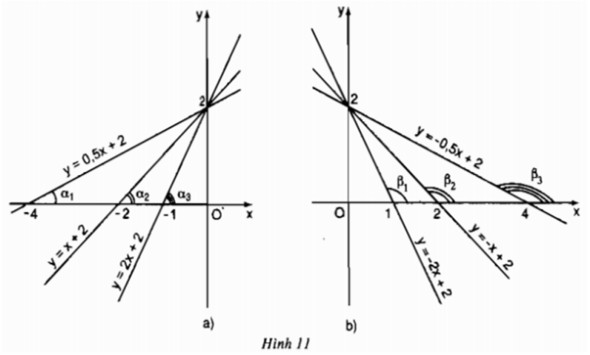
a) Hãy so sánh các góc ${\alpha _1},\,\,{\alpha _2},\,\,{\alpha _3}$ và so sánh các giá trị tương ứng của hệ số a trong các hàm số (trường hợp a > 0) rồi rút ra nhận xét.

b) Cũng làm tương tự như câu a) với trường hợp $a > 0.$

Trả lời:

a) Ta có: ${\alpha _1} < \,{\alpha _2} < {\alpha _3}$ và các giá trị tương ứng của hệ số a trong các hàm số : $0,5 < 1 < 2$

Nhận xét: Khi hệ số a dương (a > 0) thì góc tạo bởi đường thẳng $y = ax + b$ và trục $Ox$ là góc nhọn, hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 90^o

b) Ta có: ${\beta _1} < \,{\beta _2} < {\beta _3}$ và các giá trị tương ứng của hệ số a trong các hàm số: $-2 < -1 < -0,5$

Nhận xét: Khi hệ số a âm (a < 0) thì góc tạo bởi đường thẳng $y = ax + b$ và trục $Ox$ là góc tù, hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 180^o.

Dưới đây là Hướng dẫn giải bài 27 28 trang 58 sgk toán 9 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần đại số 9 kèm bài giải chi tiết bài 27 28 trang 58 sgk toán 9 tập 1 của bài §5. Hệ số góc của đường thẳng $y = ax + b (a ≠ 0)$ trong chương II – Hàm số bậc nhất cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 27 28 trang 58 sgk toán 9 tập 1

1. Giải bài 27 trang 58 sgk Toán 9 tập 1

Cho hàm số bậc nhất $y = ax + 3$:

a) Xác định hệ số góc a biết rằng đồ thị đi qua điểm $A(2:6)$.

b) Vẽ đồ thị hàm số.

Bài giải:

a) $y = ax + 3$ $(1)$

Theo giả thiết đồ thị hàm số đi qua điểm $A(2; 6)$. Thay $x=2,\ y=6$ vào $(1)$, ta được:

$ 6=2.a+3 \Leftrightarrow 6-3=2a$

$\Leftrightarrow 3=2a$ $\Leftrightarrow a=\dfrac{3}{2}$

Vậy $a=\dfrac{3}{2}$,

b) Vẽ đồ thị hàm số: $y=\dfrac{3}{2}x+3$

Cho $x=2 \Rightarrow y=\dfrac{3}{2}.2+3=3 +3 =6 \Rightarrow A(2; 6)$.

Cho $y=0 \Rightarrow 0=\dfrac{3}{2}.x+3 \Rightarrow x=-2 \Rightarrow B(-2; 0)$.

Đường thẳng đi qua hai điểm $A(2;6)$ và $B(-2;0)$ là đồ thị hàm số $y=\dfrac{3}{2}x+3$.

Đồ thị được vẽ như sau:

2. Giải bài 28 trang 58 sgk Toán 9 tập 1

Cho hàm số $y = -2x + 3$

a) Vẽ đồ thị hàm số.

b) Tính góc tạo bởi đường thẳng $y = -2x + 3$ và trục $Ox$ (làm tròn đến phút).

Bài giải:

a) Hàm số $y = -2x + 3.$

Cho $x=0 \Rightarrow y=-2.0+3=0+3=3 \Rightarrow A(0; 3)$

Cho $y=0 \Rightarrow 0=-2.x+3 \Leftrightarrow x=\dfrac{3}{2} \Rightarrow B{\left(\dfrac{3}{2}; 0\right)}$

Vẽ đường thẳng đi qua hai điểm $A(0; 3)$ và $B{\left(\dfrac{3}{2}; 0\right)}$ ta được đồ thị hàm số $y = -2x + 3.$.

Đồ thị được vẽ như sau:

b) Gọi $\alpha $ là góc giữa đường thẳng $y = -2x + 3$ và trục $Ox \Rightarrow \alpha = \widehat{ABx}$.

Xét tam giác vuông $OAB$ vuông tại $O$, ta có:

$\tan \widehat {OBA} = \dfrac{OA}{OB} = \dfrac{3}{\dfrac{3}{2}}=2$

Thực hiện bấm máy tính, ta được:

$\widehat {ABO} \approx {63^0}26’$

Lại có $\widehat {ABO}$ và $\widehat {ABx}$ là hai góc kề bù, tức là:

$\widehat {ABO} + \widehat {ABx} =180^0$

$\Leftrightarrow \widehat {ABx}=180^0 -\widehat {ABO} $

$\Leftrightarrow \widehat {ABx} \approx 180^0 -{63^0}26′ $

$\Leftrightarrow \widehat {ABx} \approx 116^0 34’$

Vậy $\alpha \approx {116^0}34’$.

Bài trước:

Luyện tập: Giải bài 23 24 25 26 trang 55 sgk Toán 9 tập 1

Bài tiếp theo:

Luyện tập: Giải bài 29 30 31 trang 59 sgk Toán 9 tập 1

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với giải bài 27 28 trang 58 sgk toán 9 tập 1!

“Bài tập nào khó đã có giaibaisgk.com“