Nội Dung
Luyện tập Bài §6. Tính chất ba đường phân giác của tam giác, chương III – Quan hệ giữa các yếu tố trong tam giác – Các đường đồng quy của tam giác, sách giáo khoa toán 7 tập hai. Nội dung bài giải bài 39 40 41 42 43 trang 73 sgk toán 7 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 7.
Lý thuyết
1. Đường phân giác của tam giác
Trong tam giác ABC tia phân giác của góc A cắt cạnh BC tại điểm M.
Đoạn thẳng AM được gọi là đường phân giác của tam giác ABC.
Đường thẳng AM cũng gọi là đường phân giác của tam giác ABC.
Mỗi tam giác có ba đường phân giác.

Tính chất:
Trong một tam giá cân đường phân giác xuất phát từ đỉnh đồng thời là đường trung tuyến ứng với cạnh đáy.
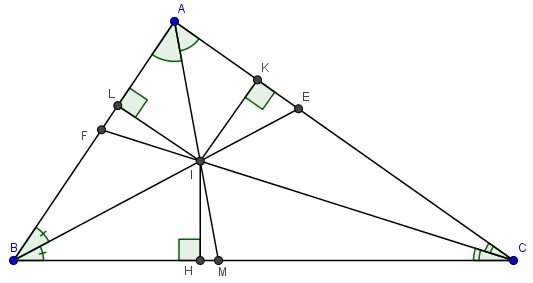
2. Tính chất ba đường phân giác của tam giác
Định lý:
Ba đường phân giác của một tam giác cùng đi qua một điểm. Điểm này cách đều ba cạnh của tam giác đó.
Giả thiết:
\(\Delta ABC\)
Hai phan giác BE, CF cắt nhau tại I.
Kết luận:
AI là tia phân giác của góc A
IH = IK = IL
Dưới đây là Hướng dẫn giải bài 39 40 41 42 43 trang 73 sgk toán 7 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Luyện tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 7 kèm bài giải chi tiết bài 39 40 41 42 43 trang 73 sgk toán 7 tập 2 của Bài §6. Tính chất ba đường phân giác của tam giác trong chương III – Quan hệ giữa các yếu tố trong tam giác – Các đường đồng quy của tam giác cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 39 trang 73 sgk Toán 7 tập 2
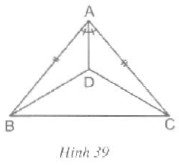
Cho hình 39.
a) Chứng minh ΔABD = ΔACD
b) So sánh góc DBC và góc DCB.
Bài giải:
a) Xét $\Delta ABD$ và $\Delta ACD$ có:
$AB=AC$ (gt)
$\widehat{BAD}=\widehat{CAD}$ (gt)
$AD$ chung
$\Rightarrow \Delta ABD=\Delta ACD\,\ (c-g-c)$ (đpcm)
b) Từ câu a) ta có: $\Delta ABD=\Delta ACD$
$\Rightarrow BD = CD$ (cạnh tương ứng)
$\Rightarrow \Delta BDC$ cân tại D
$\Rightarrow \widehat{DBC}=\widehat{DCB}$ (đpcm)
2. Giải bài 40 trang 73 sgk Toán 7 tập 2
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, I là điểm nằm trong tam giác và cách đều ba cạnh của tam giác đó. Chứng minh ba điểm A, G, I thẳng hàng.
Bài giải:

Gọi M, N lần lượt là trung điểm của BC và AC.
Vì G là trọng tâm nên G nằm trên trung tuyến AM (1).
Vì I cách đều ba cạnh của tam giác ⇒ I là giao điểm của ba đường phân giác trong của ΔABC.
ΔABC cân nên đường phân giác xuất phát từ đỉnh đối diện với đáy đồng thời là đường trung tuyến (tính chất).
Do đó, I nằm trên AM (2).
Từ (1) và (2) suy ra ba điểm A, G, I thẳng hàng (đpcm).
3. Giải bài 41 trang 73 sgk toán 7 tập 2
Hỏi trọng tâm của một tam giác đều có cách đều ba cạnh của nó hay không? Vì sao?
Bài giải:
Giả sử ∆ABC đều có trọng tâm G, các trung tuyến AN, BM, CE.
$\Rightarrow GA = \frac{2}{3},AN; GB = \frac{2}{3}.BM; GC = \frac{2}{3}.EC$ (tính chất đường trung tuyến trong tam giác)
Vì ∆ABC đều nên ba trung tuyến AN, BM, CE bằng nhau.
$\Rightarrow GA = GB = GC$ (vì cùng = $\frac{2}{3}$ các đoạn bằng nhau)
Xét $∆AMG$ và $ ∆CMG$ có:
$GM$ chung
$AM =MC$ (M là trung điểm AC)
$AG =CG$ (cmt)
$\Rightarrow \Delta AMG = \Delta CMG\,\ (c.c.c)$
$\Rightarrow \widehat{AMG}=\widehat{CMG}$
Mà \(\widehat{AMG}+\widehat{CMG}= 180^0\)
$\Rightarrow \widehat{AMG}= 90^0$
$\Rightarrow GM ⊥ AC$ tức là GM khoảng cách từ G đến AC.
Chứng minh tương tự GE, GN là khoảng cách từ G đến AB, BC.
Mà $GM =\frac{1}{3}.BM; GN = \frac{1}{3}.AN; EG = \frac{1}{3}.EC$
Và $AN = BM = EC$ nên $GM = GN = GE$.
Hay G cách đều ba cạnh của tam giác ABC.
4. Giải bài 42 trang 73 sgk Toán 7 tập 2
Chứng minh định lí: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là một tam giác cân.
Gợi ý: Trong ΔABC, nếu AD là đường trung tuyến vừa là đường phân giác thì kéo dài AD một đoạn DA, sao cho DA1 = AD.
Bài giải:

Giả sử ∆ABC có AD là phân giác \(\widehat{BAC}\) và DB = DC, ta chứng minh ∆ABC cân tại A.
Kéo dài AD một đoạn DA1 = AD.
Xét ∆ADC và ∆A1DB có:
CD = BD (gt)
DA = DA1 (cách vẽ)
$\widehat{D_1}=\widehat{D_2}$ (đối đỉnh)
$\Rightarrow ∆ADC = ∆A_1DB\,\ (c.g.c)$
$\Rightarrow BA_1=AC\,\ (1)$ (cạnh tương ứng)
Mà: $\widehat{BA_1D}=\widehat{DAC};\,\ \widehat{BAD}=\widehat{DAC}(gt)$
$\Rightarrow \widehat{BA_1D}=\widehat{BAD}$
$\Rightarrow \Delta ABA_1$ cân tại B.
$\Rightarrow AB = A_1B\,\ (2)$
Từ (1)(2) suy ra: $AB = AC$
Vậy $∆ABC$ cân tại $A$
Tức là: Nếu tam giác có một đường trung tuyến đồng thời là đường phân giác thì tam giác đó là tam giác cân
5. Giải bài 43 trang 73 sgk Toán 7 tập 2
Đố: Có hai con đường cắt nhau và cùng cắt một con sông tại hai địa điểm khác nhau (h.40).
Hãy tìm một địa điểm để xây dựng một đài quan sát sao cho khoảng cách từ đó đến hai con đường và đến bờ sông bằng nhâu.
Có tất cả mấy địa điểm như vậy?

Bài giải:
Ta hình dung hai con đường cắt nhau và cùng cắt một con sông tạo thành một tam giác ABC.

Địa điểm để xây dựng đài quan sát thỏa mãn đề bài phải là giao điểm I của 3 đường phân giác trong của tam giác ABC.
Ngoài ra, giao điểm K của hai đường phân giác ngoài của góc B và C cũng thỏa mãn đề bài.
Vậy có 2 địa điểm để xây dựng đài quan sát là I và K.
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 7 khác
- Để học tốt môn Vật lí lớp 7
- Để học tốt môn Sinh học lớp 7
- Để học tốt môn Ngữ văn lớp 7
- Để học tốt môn Lịch sử lớp 7
- Để học tốt môn Địa lí lớp 7
- Để học tốt môn Tiếng Anh lớp 7
- Để học tốt môn Tiếng Anh lớp 7 thí điểm
- Để học tốt môn Tin học lớp 7
- Để học tốt môn GDCD lớp 7
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 7 với giải bài 39 40 41 42 43 trang 73 sgk toán 7 tập 2!
“Bài tập nào khó đã có giaibaisgk.com“