Nội Dung
Hướng dẫn giải Bài §2. Đồ thị của hàm số \(y = ax^2 (a ≠ 0)\), Chương IV – Hàm số \(y = ax^2 (a ≠ 0)\). Phương trình bậc hai một ẩn, sách giáo khoa toán 9 tập hai. Nội dung bài giải bài 4 5 trang 36 37 sgk toán 9 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần đại số có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 9.
Lý thuyết
1. Nhắc lại kiến thức
Như ta đã biết, trên mặt phẳng tọa độ, đồ thị hàm số \(y=ax^2 (a\neq 0)\) là tập hợp gồm tất cả các điểm \(M(x_{M}; ax_{M}^{2})\). Để xác định một điểm thuộc đồ thị, ta lấy một giá trị của x làm hoành độ và thay vào phương trình \(y=ax^2\) để tìm ra giá trị tung độ.
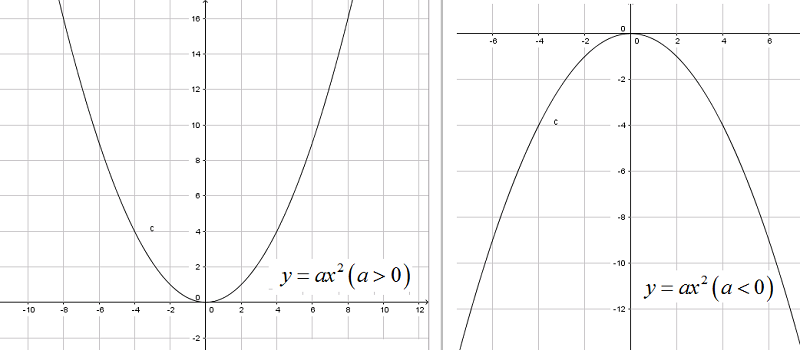
2. Nhận xét
Từ đó, ta rút ra được một số nhận xét sau:
Vì \(x=0\Rightarrow y=0\) nên đồ thị luôn qua gốc tọa độ \(O(0;0)\)
Đồ thị hàm số \(y=ax^2 (a\neq 0)\) là một đường cong đi qua gốc tọa độ và nhận trục Oy là trục đối xứng. Đường cong đó gọi là một Parabol với đỉnh O.
Nếu (a>0) thì đồ thị nằm phía trên trục hoành, O là điểm thấp nhấp của đồ thị.
Nếu (a<0) thì đồ thị nằm phía dưới trục hoành, O là điểm cao nhấp của đồ thị.
Chú ý: Vì đồ thị \(y=ax^2 (a\neq 0)\) luôn đi qua gốc tọa độ và nhận trục Oy làm trục đối xứng nên để vẽ đồ thị này, ta chỉ cần tìm một số điểm bên phải trục Oy rồi lấy đối xứng của chúng qua Oy.
Dưới đây là phần Hướng dẫn trả lời các câu hỏi có trong bài học cho các bạn tham khảo. Các bạn hãy đọc kỹ câu hỏi trước khi trả lời nhé!
Câu hỏi
1. Trả lời câu hỏi 1 trang 34 sgk Toán 9 tập 2
Hãy nhận xét một vài đặc điểm của đồ thị này bằng cách trả lời các câu hỏi sau (h.6):

– Đồ thị nằm ở phía trên hay phía dưới trục hoành ?
– Vị trí của cặp điểm \(A, A’\) đối với trục \(Oy\) ? Tương tự đối với các điểm \(B, B’\) và \(C, C’ \)?
– Điểm nào là điểm thấp nhất của đồ thị ?
Trả lời:
– Đồ thị nằm ở phía trên trục hoành
– Các cặp điểm \(A\) và \(A’; B\) và \(B’; C\) và \(C’\) đối xứng nhau qua trục tung \(Oy\)
– Điểm \(O (0;0)\) là điểm thấp nhất của đồ thị.
2. Trả lời câu hỏi 2 trang 34 sgk Toán 9 tập 2
Nhận xét một vài đặc điểm của đồ thị và rút ra những kết luận tương tự như đã làm với hàm số \(y = 2{x^2}.\)
Trả lời:
– Đồ thị nằm ở phía dưới trục hoành.
– Các cặp điểm \(P\) và \(P’; M\) và \(M’; N\) và \(N’\) đối xứng nhau qua trục tung \(Oy\)
– Điểm \(O (0;0)\) là điểm cao nhất của đồ thị.
3. Trả lời câu hỏi 3 trang 35 sgk Toán 9 tập 2
Cho hàm số \(y = \displaystyle{{ – 1} \over 2}{x^2}\)
a) Trên đồ thị của hàm số này, xác định điểm D có hoành độ bằng \(3.\) Tìm tung độ của điểm D bằng hai cách: bằng đồ thị; bằng cách tính \(y\) với \(x = 3\). So sánh hai kết quả.
b) Trên đồ thị làm số này, xác định điểm có tung độ bằng \(-5.\) Có mấy điểm như thế ? Không làm tính, hãy ước lượng giá trị hoành độ của mỗi điểm.
Trả lời:

a) Từ đồ thị, ta xác định được tung độ của điểm D là \(\displaystyle{{ – 9} \over 2}\)
Với \(x = 3\) ta có: \(y = \displaystyle{{ – 1} \over 2}{x^2} = {\displaystyle{ – 1} \over 2}{.3^2} = {{ – 9} \over 2}\)
⇒ Hai kết quả bằng nhau.
b) Có 2 điểm có tung độ bằng \(-5\) là điểm \(M\) và điểm \(N\) (hình vẽ).
Giá trị của hoành độ điểm \(M\) là \( x_M\approx 3,2\) và hoành độ điểm \(N\) là \( x_N\approx -3,2\)
Dưới đây là Hướng dẫn giải bài 4 5 trang 36 37 sgk toán 9 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần đại số 9 kèm bài giải chi tiết bài 4 5 trang 36 37 sgk toán 9 tập 2 của Bài §2. Đồ thị của hàm số \(y = ax^2 (a ≠ 0)\) trong Chương IV – Hàm số \(y = ax^2 (a ≠ 0)\). Phương trình bậc hai một ẩn cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
1. Giải bài 4 trang 36 sgk Toán 9 tập 2
Cho hai hàm số: \(y = \dfrac{3}{2}{x^2},y = – \dfrac{3}{2}{x^2}\). Điền vào những ô trống của các bảng sau rồi vẽ hai đồ thị trên cùng một mặt phẳng tọa độ.
| $x$ | -2 | -1 | 0 | 1 | 2 |
| $y = \frac{3}{2}x^2$ |
| $x$ | -2 | -1 | 0 | 1 | 2 |
| $y = -\frac{3}{2}x^2$ |
Nhận xét về tính đối xứng của hai đồ thị đối với trục \(Ox\).
Bài giải:
♦ Thực hiện phép tính sau:
+) Đối với hàm số \(y=\dfrac{3}{2}x^2\):
\(x=-2 \Rightarrow y=\dfrac{3}{2}.(-2)^2=\dfrac{3}{2}.4=6\).
\(x=-1 \Rightarrow y=\dfrac{3}{2}.(-1)^2=\dfrac{3}{2}.1=\dfrac{3}{2}\).
\(x=0 \Rightarrow y=\dfrac{3}{2}.0=0\).
\(x=1 \Rightarrow y=\dfrac{3}{2}.1^2=\dfrac{3}{2}\).
\(x=2 \Rightarrow y=\dfrac{3}{2}.2^2=\dfrac{3}{2}.4=6\)
+) Đối với hàm số \(y=-\dfrac{3}{2}x^2\):
\(x=-2 \Rightarrow y=-\dfrac{3}{2}.(-2)^2=-\dfrac{3}{2}.4=-6\).
\(x=-1 \Rightarrow y=-\dfrac{3}{2}.(-1)^2=-\dfrac{3}{2}.1=-\dfrac{3}{2}\).
\(x=0 \Rightarrow y=-\dfrac{3}{2}.0=0\).
\(x=1 \Rightarrow y=-\dfrac{3}{2}.1^2=-\dfrac{3}{2}\).
\(x=2 \Rightarrow y=-\dfrac{3}{2}.2^2=-\dfrac{3}{2}.4=-6\)
Ta được bảng sau:
| $x$ | -2 | -1 | 0 | 1 | 2 |
| $y = \frac{3}{2}x^2$ | 6 | $\frac{3}{2}$ | 0 | $\frac{3}{2}$ | 6 |
| $y = -\frac{3}{2}x^2$ | -6 | $-\frac{3}{2}$ | 0 | $-\frac{3}{2}$ | -6 |
♦ Vẽ đồ thị:
+) Vẽ đồ thị hàm số \(y=\dfrac{3}{2}x^2\)
Quan sát bảng trên ta thấy đồ thị đi qua các điểm:
\(A(-2; 6);\ B{\left(-1; \dfrac{3}{2}\right)};\ O(0; 0);\ C{\left(1; \dfrac{3}{2}\right)};\ D(2; 6)\)
+) Vẽ đồ thị hàm số \(y=-\dfrac{3}{2}x^2\)
Quan sát bảng trên ta thấy đồ thị đi qua các điểm:
\(A'(-2; -6);\ B'{\left(-1; -\dfrac{3}{2}\right)};\ O(0; 0);\)
\(\ C'{\left(1; -\dfrac{3}{2}\right)};\ D'(2; -6)\)

Nhận xét: Đồ thị của hai hàm số đối xứng với nhau qua trục \(Ox\).
2. Giải bài 5 trang 37 sgk Toán 9 tập 2
Cho ba hàm số:
\(y = \dfrac{1}{2}{x^2};\ y = {x^2};\ y = 2{x^2}\).
a) Vẽ đồ thị của ba hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm ba điểm \(A,\ B,\ C\) có cùng hoành độ \(x = -1,5\) theo thứ tự nằm trên ba đồ thị. Xác định tung độ tương ứng của chúng.
c) Tìm ba điểm \(A’,\ B’,\ C’\) có cùng hoành độ \(x = 1,5\) theo thứ tự nằm trên ba đồ thị. Kiểm tra tính đối xứng của \(A\) và \(A’\), \(B\) và \(B’\), \(C\) và \(C’\).
d) Với mỗi hàm số trên, hãy tìm giá trị của \(x\) để hàm số đó có giá trị nhỏ nhất.
Bài giải:
a) ♦ Vẽ đồ thị hàm số \(y = \dfrac{1}{2}{x^2}\)
Cho \(x=1 \Rightarrow y=\dfrac{1}{2}\). Đồ thị đi qua \({\left(1; \dfrac{1}{2} \right)}\).
Cho \(x=-1 \Rightarrow y=\dfrac{1}{2}\). Đồ thị đi qua \({\left(-1; \dfrac{1}{2} \right)}\).
Cho \(x=2 \Rightarrow y=\dfrac{1}{2}. 2^2=2\). Đồ thị hàm số đi qua điểm \((2; 2)\).
Cho \(x=-2 \Rightarrow y=\dfrac{1}{2}.(-2)^2=2\). Đồ thị hàm số đi qua điểm \((-2; 2)\).
Đồ thị hàm số \(y=\dfrac{1}{2}x^2\) là parabol đi qua gốc tọa độ và các điểm trên.
♦ Vẽ đồ thị hàm số \(y=x^2\).
Cho \(x=1 \Rightarrow y=1\). Đồ thị đi qua \((1; 1)\).
Cho \(x=-1 \Rightarrow y=(-1)^2\). Đồ thị đi qua \((-1; 1)\).
Cho \(x=2 \Rightarrow y=2^2=4\). Đồ thị hàm số đi qua điểm \((2; 4)\).
Cho \(x=-2 \Rightarrow y=(-2)^2=4\). Đồ thị hàm số đi qua điểm \((-2; 4)\).
Đồ thị hàm số \(y=x^2\) là parabol đi qua gốc tọa độ và các điểm trên.
♦ Vẽ đồ thị hàm số \(y=2x^2\).
Cho \(x=1 \Rightarrow y=2.1^2=2\). Đồ thị đi qua \((1; 2)\).
Cho \(x=-1 \Rightarrow y=2.(-1)^2\). Đồ thị đi qua \((-1; 2)\).
Cho \(x=2 \Rightarrow y=2.2^2=8\). Đồ thị hàm số đi qua điểm \((2; 8)\).
Cho \(x=-2 \Rightarrow y=2.(-2)^2=8\). Đồ thị hàm số đi qua điểm \((-2; 8)\).
Đồ thị hàm số \(y=2x^2\) là parabol đi qua gốc tọa độ và các điểm trên.

b) Xác định điểm P trên trục Ox có hoành độ \(x = – 1,5\). Qua P kẻ đường thẳng song song với trục Oy, nó cắt các đồ thị \(y = \dfrac{1}{2}{x^2};y = {x^2};y = 2{x^2}\) lần lượt tại \(A;B;C\)
Gọi \({y_A},{y_B},{y_C}\) lần lượt là tung độ các điểm \(A,\ B,\ C\). Ta có:
\(\eqalign{
& {y_A} = {1 \over 2}{( – 1,5)^2} = {1 \over 2}.2,25 = 1,125 \cr
& {y_B} = {( – 1,5)^2} = 2,25 \cr
& {y_C} = 2{( – 1.5)^2} = 2.2,25 = 4,5 \cr} \)
c) Xác định điểm \(P’\) trên trục Ox có hoành độ \(x = 1,5\). Qua \(P’\) kẻ đường thẳng song song với trục Oy, nó cắt các đồ thị \(y = \dfrac{1}{2}{x^2};y = {x^2};y = 2{x^2}\) lần lượt tại \(A’;B’;C’\)
Gọi \({y_{A’}},{y_{B’}},{y_{C’}}\) lần lượt là tung độ các điểm \(A’, B’, C’\) . Ta có:
\(\eqalign{
& {y_{A’}} = {1 \over 2}{(1,5)^2} = {1 \over 2}.2,25 = 1,125 \cr
& {y_{B’}} = {(1,5)^2} = 2,25 \cr
& {y_{C’}} = 2{(1.5)^2} = 2.2,25 = 4,5 \cr} \)
Kiểm tra tính đối xứng: \(A\) và \(A’\), \(B\) và \(B’\), \(C\) và \(C’\) đối xứng với nhau qua trục tung \(Oy\).
d) Với mỗi hàm số đã cho ta đều có hệ số \(a > 0\) nên O là điểm thấp nhất của đồ thị.
Vậy với \(x = 0\) thì các hàm số trên đều có giả trị nhỏ nhất \(y=0.\)
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 9 khác
- Để học tốt môn Vật lí lớp 9
- Để học tốt môn Sinh học lớp 9
- Để học tốt môn Ngữ văn lớp 9
- Để học tốt môn Lịch sử lớp 9
- Để học tốt môn Địa lí lớp 9
- Để học tốt môn Tiếng Anh lớp 9
- Để học tốt môn Tiếng Anh lớp 9 thí điểm
- Để học tốt môn Tin học lớp 9
- Để học tốt môn GDCD lớp 9
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với giải bài 4 5 trang 36 37 sgk toán 9 tập 2!
“Bài tập nào khó đã có giaibaisgk.com“
