Nội Dung
Hướng dẫn giải Bài §7. Định lí, chương I – Đường thẳng vuông góc. Đường thẳng song song, sách giáo khoa toán 7 tập một. Nội dung bài giải bài 49 50 trang 101 sgk toán 7 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 7.
Lý thuyết
1. Định lý
Định lý là khẳng định suy ra từ những khẳng định được coi là đúng.
Mỗi định lý thường được phát biểu dưới dạng “Nếu $A$ thì $B$”.
$A$ gọi là giả thiết, $B$ gọi là kết luận.
Giả thiết và kết luận được viết tắt tương ứng là $GT$ và $KL$.
2. Chứng minh định lý
Chứng minh định lý là dùng lập luận để từ giả thiết suy ra kết luận.
Để chứng minh định lý ta làm như sau:
– Vẽ hình.
– Ghi giả thiết, kết luận.
– Nêu các bước chứng minh. Mỗi bước gồm một khẳng định và căn cứ của khẳng định đó.
3. Ví dụ minh họa
Trước khi đi vào giải bài 49 50 trang 101 sgk toán 7 tập 1, chúng ta hãy tìm hiểu các ví dụ điển hình sau đây:
Ví dụ 1:
Điền vào chỗ trống bằng những nội dung thích hợp để được các định lý:
a. Nếu M là trung điểm của đoạn AB thì….
b. Nếu …. Thì \(MA = MB = \frac{1}{2}AB.\)
c. Nếu tia Ot là tia phân giác của góc xOy thì ….
d. Nếu …..thì \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}\widehat {xOy}\)
e. Nếu \(\widehat {xOy}\) và \(\widehat {x’Oy’}\) là hai góc đối đỉnh thì …..
Bài giải:
a. Có thể điền vào chỗ trống theo vài cách sau đây:
M nằm giữa A và B
MA= MB
\(MA = MB = \frac{1}{2}AB\)
M nằm giữa A,B và MA = MB
MA + MB = AB và MA = MB
b. Chỉ có một cách điền vào chỗ trống: M là trung điểm của đoạn AB.
c. Có thể điền vào chỗ trống theo vài cách sau đây:
Ot nằm giữa hai tia Ox và Oy.
\(\widehat {xOt} = \widehat {tOy}\)
\(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}\widehat {xOy}\)
Ot nằm giữa hai tia Ox, Oy và \(\widehat {xOy} = \widehat {tOy}\)
\(\widehat {xOy} = \widehat {tOy}\) và \(\widehat {xOt} + \widehat {tOy} + \widehat {tOy} = \widehat {xOy}\)
d. Chỉ có một cách điền vào chỗ trống: Ot là tia phân giác của góc xOy.
e. Có thể điền như sau: Chúng bằng nhau.
Nhận xét: Ở câu a, c, e còn có thể điền theo nội dung khác.
Ví dụ 2:
Cho mệnh đề: “Số đo của góc tạo bởi tia phân giác với mỗi cạnh của góc bằng nửa số đo của góc ấy”.
a. Phát biểu mệnh đề trên dưới dạng: “Nếu…. thì….”
b. Hãy chứng minh mệnh đề đó.
Bài giải:
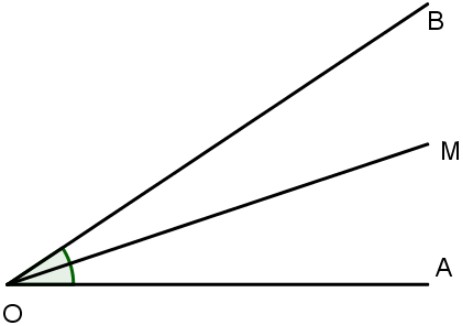
a. Nếu OM là tia phân giác của góc AOB thì:
\(\widehat {AOM} = \widehat {MOB} = \frac{1}{2}\widehat {AOB}\)
b. Chứng minh OM là phân giác của góc AOB nên:
\(\left. \begin{array}{l}\widehat {MOA} + \widehat {MOB} = \widehat {AOB}\\\widehat {MOA} = \widehat {MOB}\end{array} \right\}2\widehat {MOA} = \widehat {APB} \Rightarrow \widehat {MOA} = \frac{1}{2}\widehat {AOB}\)
Mà \(\widehat {MOA} = \widehat {MOB}\) nên \(\widehat {MOA} = \widehat {MOB} = \frac{1}{2}\widehat {AOB}\)
Ví dụ 3:
Cho mệnh đề sau: “C là một điểm nằm trên đoạn thẳng AB. Gọi M là trung điểm của đoạn AC, N là trung điểm của đoạn BC thế thì \(MN = \frac{1}{2}AB.\) Hãy chứng minh.
Bài giải:
Ta có M là trung điểm của đoạn AC nên M thuộc tia AC, tương tự N thuộc tia BC.
Hai tia CA, CB là hai tia đối nhau (do C nằm giữa AB) \( \Rightarrow \) C nằm giữa M và N ( Hình bên)

Lại có: \(\left. \begin{array}{l}MC = \frac{1}{2}AC\\NC = \frac{1}{2}BC\end{array} \right\} \Rightarrow MC + NC = \frac{1}{2}AC + \frac{1}{2}BC = \frac{1}{2}(AC + BC) = \frac{1}{2}AB\)
Hay \(MN = \frac{1}{2}AB\)
Ví dụ 4:
Chứng minh định lý: “Hai tia phân giác của hai góc kề bù tạo thành một góc vuông”.
Bài giải:

Cho \(\widehat {AOB}\) và \(\widehat {BOC}\) là hai góc kề bù. OM, ON lần lượt là các tia phân giác của \(\widehat {ACB}\) và \(\widehat {BOC.}\)
Chứng minh \(\widehat {MON} = {90^0}.\)
Ta có: OM là tia phân giác của góc AOB nên tia OM nằm giữa hai tia OA và OB và \(\widehat {MOB} = \frac{1}{2}AOB.\)
Tương tự ON là tia phân giác của góc BOC nên ON nằm giữa hai tia OB và OC và \(\widehat {BON} = \frac{1}{2}BOC.\)
Lại có: \(\widehat {AOB}\) và \(\widehat {BOC}\) là hai góc kề bù nên tia OB nằm giữa hai tia OA và OC \( \Rightarrow \) OB nằm giữa hai tia OM và ON nên:
\(\widehat {MON} = \widehat {MOB} + \widehat {BON} = \frac{1}{2}\left( {\widehat {AOB} + \widehat {BOC}} \right) = \frac{1}{2} – {180^0} = {90^0}\)
Dưới đây là phần Hướng dẫn trả lời các câu hỏi có trong bài học cho các bạn tham khảo. Các bạn hãy đọc kỹ câu hỏi trước khi trả lời nhé!
Câu hỏi
1. Trả lời câu hỏi 1 trang 99 sgk Toán 7 tập 1
Ba tính chất ở bài 6 là ba định lí. Em hãy phát biểu lại ba định lí đó.
Trả lời:
Ta có : ba định lí là:
– Hai đường thẳng phân biệt cùng vuông góc với nột đường thẳng thứ ba thì chúng song song với nhau.
– Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
– Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.
2. Trả lời câu hỏi 2 trang 100 sgk Toán 7 tập 1
a) Hãy chỉ ra giả thiết và kết luận của định lí: “Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau”.
b) Vẽ hình minh họa định lí trên và viết, giả thiết kết luận bằng kí hiệu.
Trả lời:
Ta có :
a) Giả thiết : Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba.
Kết luận : chúng song song với nhau.
b) Hình vẽ minh họa:

Giả thiết: $a//c ; b//c$.
Kết luận: $a//b$.
Dưới đây là Hướng dẫn giải bài 49 50 trang 101 sgk toán 7 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 7 kèm bài giải chi tiết bài 49 50 trang 101 sgk toán 7 tập 1 của bài §7. Định lí trong chương I – Đường thẳng vuông góc. Đường thẳng song song cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
1. Giải bài 49 trang 101 sgk Toán 7 tập 1
Hãy chỉ ra giả thiết và kết luận của các định lí sau:
a) Nếu một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song.
b) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau.
Bài giải:
a) Giả thiết: Một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau.
Kết luận: Hai đường thẳng đó song song.
b) Giả thiết: Một đường thẳng cắt hai đường thẳng song song.
Kết luận: Hai góc so le trong bằng nhau.
2. Giải bài 50 trang 101 sgk Toán 7 tập 1
a) Hãy viết kết luận của định lí sau bằng cách điền vào chỗ trống (…):
Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì …
b) Vẽ hình minh họa định lí đó và viết giả thiết, kết luận bằng kí hiệu.
Bài giải:
a) Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
b) Định lí được minh họa bằng hình vẽ sau:

Giả thiết và kết luận của định lí trên được ghi bằng kí hiệu như sau:
$GT: a \perp c; b \perp c$
$KL: a // b$.

Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 7 khác
- Để học tốt môn Vật lí lớp 7
- Để học tốt môn Sinh học lớp 7
- Để học tốt môn Ngữ văn lớp 7
- Để học tốt môn Lịch sử lớp 7
- Để học tốt môn Địa lí lớp 7
- Để học tốt môn Tiếng Anh lớp 7
- Để học tốt môn Tiếng Anh lớp 7 thí điểm
- Để học tốt môn Tin học lớp 7
- Để học tốt môn GDCD lớp 7
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 7 với giải bài 49 50 trang 101 sgk toán 7 tập 1!
“Bài tập nào khó đã có giaibaisgk.com“
