Nội Dung
Hướng dẫn giải Bài §9. Vẽ đoạn thẳng cho biết độ dài, chương I – Đoạn thẳng, sách giáo khoa toán 6 tập một. Nội dung bài giải bài 53 54 55 56 57 58 59 trang 124 sgk toán 6 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 6.
Lý thuyết
1. Vẽ đoạn thẳng trên tia
Ví dụ 1:
Trên tia $Ox$, hãy vẽ đoạn thẳng $OM$ có độ dài bằng $2cm.$
Bài giải:
Cách vẽ: Mút O đã biết. Ta vẽ mút M như sau:
Đặt cạnh của thước nằm trên tia Ox sao cho vạch số 0 của thước trùng với gốc O của tia
Vạch số 2 (cm) của thước sẽ cho ta điểm M. Đoạn thẳng OM là đoạn thẳng phải vẽ.
Nhận xét: Trên tia Ox bao giờ cũng vẽ được một và chỉ một điểm M sao OM = a (đơn vị dài).
Ví dụ 2:
Cho đoạn thẳng AB (h.55). Hãy vẽ đoạn thẳng CD sao cho CD = AB.
Bài giải:

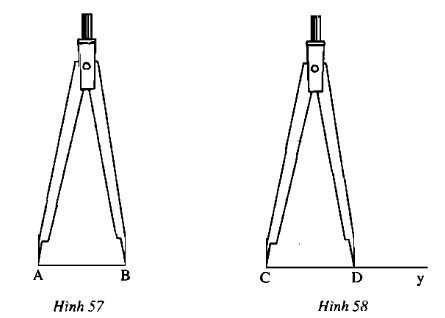
Vẽ một tia Cy bất kì (h.56). Khi đó, ta đã biết mút C của đoạn thẳng CD. Ta vẽ mút D như sau:
– Đặt compa sao cho một mũi nhọn trùng với mút A, mũi kia trùng với mút B của đoạn thẳng AB cho trước.
– Giữ độ mở của compa không đổi, đặt compa sao cho một mũi nhọn trùng với góc C của tia Cy, mũi kia nằm trên tia vẽ cho ta mút D và CD là đoạn thẳng phải vẽ.
2. Vẽ hai đoạn thẳng trên tia
Ví dụ 3:
Trên tia Ox, hãy vẽ hai đoạn thẳng OM và ON biết OM = 2cm, ON = 3cm. Trong ba điểm O, M, N điểm nào giữa hai điểm còn lại?
Bài giải:
Sau khi vẽ hai điểm M và N (h.59) ta thấy điểm M nằm giữa hai điểm O và N (vì 2cm < 3cm).

Nhận xét: Trên tia Ox, OM = a, ON = b (h.60), nếu 0 < a < b thì điểm M nằm giữa hai điểm O và N.

Dưới đây là Hướng dẫn giải bài 53 54 55 56 57 58 59 trang 124 sgk toán 6 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học kèm bài giải chi tiết bài 53 54 55 56 57 58 59 trang 124 sgk toán 6 tập 1 của bài §9. Vẽ đoạn thẳng cho biết độ dài trong chương I – Đoạn thẳng cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 53 trang 124 sgk Toán 6 tập 1
Trên tia $Ox$ vẽ hai đoạn thẳng $OM$ và $ON$ sao cho $OM = 3cm, ON = 6cm$. Tính $MN$. So sánh $OM$ và $MN.$
Bài giải:

– Tính $MN$:
So sánh độ dài của hai đoạn thẳng $OM$ và $ON$, ta thấy $OM < ON$. Do đó $M$ nằm giữa hai điểm $O$ và $N$. Ta có:
$OM + MN = ON$
$⇒ MN = ON – OM = 6 – 3 = 3.$
Vậy $MN = 3cm.$
– So sánh $OM$ và $MN$:
Ta có:
$\left.\begin{matrix} OM = 3cm\\ MN = 3cm\end{matrix}\right\}$ $⇒ OM = MN.$
2. Giải bài 54 trang 124 sgk Toán 6 tập 1
Trên tia $Ox$ vẽ ba đoạn thẳng $OA, OB, OC$ sao cho $OA = 2cm, OB = 5cm, OC = 8cm$. So sánh $BC$ và $BA.$
Bài giải:

So sánh độ dài của hai đoạn thẳng $OB$ và $OC$:
Ta thấy $OB < OC$. Do đó $B$ nằm giữa hai điểm $O$ và $C$. Ta có:
$OB + BC = OC$
$⇒ BC = OC – OB = 8 – 5 = 3.$
Vậy $BC = 3cm.$ (1)
Tương tự ta thấy: $OA < OB$ nên $A$ nằm giữa hai điểm $O$ và $B$, ta có:
$OA + AB = OB $
$⇒ AB = OB – OA = 5 – 2 = 3$
Vậy $AB = 3cm$. (2)
Từ (1) và (2) suy ra $AB = BC.$
3. Giải bài 55 trang 124 sgk Toán 6 tập 1
Gọi $A, B$ là hai điểm trên tia $Ox$. Biết $OA = 8cm, AB = 2cm$, tính $OB$? Bài toán có mấy đáp số?
Bài giải:
Có hai trường hợp:
– Trường hợp điểm $B$ nằm giữa hai điểm $O$ và $A$.

Điểm $B$ nằm giữa hai điểm $O$ và $A$, ta có:
$OB + BA = OA$
$⇒ OB = OA – BA = 8 – 2 = 6.$
Vậy $OB = 6cm.$
– Trường hợp $A$ nằm giữa hai điểm $O$ và $B$.

Vì $A$ nằm giữa hai điểm $O$ và $B$ nên ta có:
$OA + AB = OB$
$⇒ OB = 8 + 2 = 10$
Vậy $OB = 10 cm.$
Bài toán có hai đáp số: $OB = 6cm$, hoặc $OB = 10cm.$
4. Giải bài 56 trang 124 sgk Toán 6 tập 1
Cho đoạn thẳng $AB$ dài $4cm$. Trên tia $AB$ lấy điểm $C$ sao cho $AC = 1cm.$
a) Tính $CB.$
b) Lấy điểm $D$ thuộc tia đối của tia $BC$ sao cho $BD = 2cm$. Tính $CD$?
Bài giải:
a) Theo đề bài, $AC < AB$ nên $C$ nằm giữa hai điểm $A$ và $B.$

Ta có $AC + CB = AB$
$⇒ CB = AB – AC = 4 – 1 = 3$
Vậy $CB = 3cm.$
b) Theo đề bài, điểm $B$ là gốc của hai tia đối nhau $BC$ và $BD$ nên $B$ nằm giữa hai điểm $C$ và $D$.
![]()
Ta có $CD = CB + BD = 3 + 2 = 5$
Vậy $CD = 5cm.$
5. Giải bài 57 trang 124 sgk Toán 6 tập 1
Đoạn thẳng $AC$ dài $5cm$. Điểm $B$ nằm giữa $A$ và $C$ sao cho $BC = 3cm.$
a) Tính $AB$.
b) Trên tia đối của tia $BA$ lấy điểm $D$ sao cho $BD = 5cm$. So sánh $AB$ và $CD$.
Bài giải:
a) Theo đề bài, điểm $B$ nằm giữa $A$ và $C$ nên ta có:
![]()
$AB + BC = AC$
$⇒ AB = AC – BC = 5 – 3 = 3$
Vậy $AB = 2cm.$
b) Theo đề bài, $BC < BD$ nên điểm $B$ nằm giữa hai điểm $C$ và $D$.

Ta có $BC + CD = BD$
$⇒ CD = BD – BC = 5 – 3 = 2.$
Vậy $CD = 2cm$
Do đó $AB = CD = 2cm.$
6. Giải bài 58 trang 124 sgk Toán 6 tập 1
Vẽ đoạn thẳng $AB$ dài $3,5cm$. Nói cách vẽ.
Bài giải:
Có 2 cách vẽ:
– Chỉ dùng thước kẻ:

+ Vẽ tia $Ax$ bất kì.
+ Đặt cạnh thước (phần có vạch đo kích thước) nằm trên tia $Ax$ sao cho vạch số $0$ của thước trùng với gốc $A$ của tia.
+ Vạch số $3,5cm$ của thước sẽ cho ta điểm $B$. Đoạn thẳng $AB$ là đoạn thẳng cần vẽ.
– Dùng thước kẻ và compa:

+ Vẽ đường thẳng $a$ bất kì.
+ Trên đường thẳng $a$ lấy một điểm $A$ bất kì. Dùng compa quay một vòng tròn tâm $A$, bán kính $3,5cm.$
+ Đường tròn sẽ cắt đường thẳng $a$ tại $2$ điểm. Hai điểm này sẽ là điểm $B$ cần tìm (bạn chọn lấy điểm nào cũng được).
7. Giải bài 59 trang 124 sgk Toán 6 tập 1
Trên tia $Ox$ cho ba điểm $M, N, P$ biết $OM = 2cm, ON = 3cm, OP = 3,5cm$. Hỏi trong ba điểm $M, N, P$ thì điểm nào nằm giữa hai điểm còn lại? Vì sao?
Bài giải:

Theo đề bài, trên tia $Ox$:
$OM < ON$ nên $M$ nằm giữa $O$ và $N$.
Ta có $OM + MN = ON$
$⇒ MN = ON – OM = 3 – 2 = 1$
Vậy $MN = 1cm$
$OM < OP$ nên $M$ nằm giữa $O$ và $P$.
Ta có $OM + MP = OP$
$⇒ MP = OP – OM = 3,5 – 2 = 1,5$
Vậy $MP = 1,5cm$
Trên tia $Mx$ ta có $MN < MP$ nên điểm $N$ nằm giữa hai điểm $M$ và $P.$
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 6 khác
- Để học tốt môn Vật lí lớp 6
- Để học tốt môn Sinh học lớp 6
- Để học tốt môn Ngữ văn lớp 6
- Để học tốt môn Lịch sử lớp 6
- Để học tốt môn Địa lí lớp 6
- Để học tốt môn Tiếng Anh lớp 6
- Để học tốt môn Tiếng Anh lớp 6 thí điểm
- Để học tốt môn Tin học lớp 6
- Để học tốt môn GDCD lớp 6
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 6 với giải bài 53 54 55 56 57 58 59 trang 124 sgk toán 6 tập 1!
“Bài tập nào khó đã có giaibaisgk.com“
