Nội Dung
Bài Ôn tập Chương IV – Hàm số \(y = ax^2 (a ≠ 0)\). Phương trình bậc hai một ẩn, sách giáo khoa toán 9 tập hai. Nội dung bài giải bài 54 55 56 57 58 59 60 61 62 63 64 65 66 trang 63 64 sgk toán Hướng dẫn giải 9 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần đại số có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 9.
Lý thuyết
1. Đồ thị hàm số \(y=ax^2 (a\neq 0)\)
Đồ thị hàm số \(y=ax^2 (a\neq 0)\) là tập hợp gồm tất cả các điểm \(M(x_{M}; ax_{M}^{2})\). Để xác định một điểm thuộc đồ thị, ta lấy một giá trị của x làm hoành độ và thay vào phương trình \(y=ax^2\) để tìm ra giá trị tung độ.
2. Phương trình bậc hai
Phương trình bậc hai một ẩn (gọi tắt là phương trình bậc hai) là phương trình có dạng \(ax^2+bx+c=0\)
Trong đó, x là ẩn; các hệ số a, b, c là các số cho trước và \(a\neq 0\)
3. Công thức nghiệm của phương trình bậc hai
Với phương trình \(ax^2+bx+c=0 (a\neq 0)\) và biệt thức \(\Delta =b^2-4ac\):
\(\Delta>0\) thì phương trình có 2 nghiệm phân biệt:
\(x_{1}=\frac{-b+\sqrt{\Delta }}{2a}\); \(x_{2}=\frac{-b-\sqrt{\Delta }}{2a}\)
\(\Delta=0\) thì phương trình có nghiệm kép \(x=x_{1}=x_{2}=-\frac{b}{2a}\)
\(\Delta<0\) phương trình vô nghiệm.
4. Công thức nghiệm thu gọn
Với các phương trình bậc hai \(ax^2+bx+c=0(a\neq 0)\) và \(b=2b’\), \(\Delta ‘=b’^2-ac\) thì:
Nếu \(\Delta ‘>0\) thì phương trình có hai nghiệm phân biệt
\(x_{1}=\frac{-b’+\sqrt{\Delta ‘}}{a}; x_{2}=\frac{-b’-\sqrt{\Delta ‘}}{a}\)
Nếu \(\Delta ‘=0\) thì phương trình có nghiệm kép \(x=\frac{-b’}{a}\)
Nếu \(\Delta ‘<0) thì phương trình vô nghiệm.
5. Định lí Vi ét và ứng dụng
Phương trình bậc hai \(ax^2+bx+c=0 (a\neq 0)\) có 2 nghiệm phân biệt
\(x_1=\frac{-b+\sqrt{\Delta }}{2a}; x_2=\frac{-b-\sqrt{\Delta }}{2a}\)
Ta có: \(x_1+x_2=\frac{-2b+\sqrt{\Delta }-\sqrt{\Delta }}{2a}=-\frac{b}{a}\)
\(x_1.x_2=\frac{b^2-\Delta }{4a^2}=\frac{4ac}{4a^2}=\frac{c}{a}\)
Định lý Vi-ét: Nếu \(x_1;x_2\) là hai nghiệm của phương trình \(ax^2+bx+c=0 (a\neq 0)\) thì:
\(x_1+x_2=-\frac{b}{a}\) và \(x_1.x_2=\frac{c}{a}\)
Tổng quát:
– Nếu phương trình \(ax^2+bx+c=0 (a\neq 0)\) có \(a+b+c=0\) thì phương trình có một nghiệm là \(x_1=1\) và nghiệm kia là \(x_2=\frac{c}{a}\).
– Nếu phương trình \(ax^2+bx+c=0 (a\neq 0)\) có \(a-b+c=0\) thì phương trình có một nghiệm là \(x_1=-1\) và nghiệm kia là \(x_2=-\frac{c}{a}\).
6. Các phương trình quy về phương trình bậc hai (phương trình trùng phương, phương trình có ẩn ở mẫu, phương trình tích…)
a) Phương trình trùng phương
Phương trình trùng phương là phương trình có dạng: \(ax^4+bx^2+c=0 (a\neq 0)\)
b) Phương trình chứa ẩn ở mẫu
Các bước để giải phương trình chứa ẩn ở mẫu đã học ở lớp 8
– Bước 1: Tìm điều kiện xác định của phương trình
– Bước 2: Quy đồng hai vế rồi khử mẫu
– Bước 3: Giải phương trình vừa nhận được
– Bước 4: So sánh điều kiện ban đầu rồi kết luận nghiệm
c) Phương trình tích
Nhắc lại kiến thức đã học ở lớp dưới: Biến đổi phương trình về dạng \(A.B.C…..=0\) rồi suy ra hoặc \(A=0\) hoặc \(B=0\) hoặc…..
7. Giải toán bằng phương pháp lập phương trình
Để giải bài toán bằng cách lập phương trình, chúng ta làm theo các bước sau:
– Bước 1: Lập phương trình.
+ Chọn ẩn và đặt điều kiện cho ẩn.
+ Biểu đạt các đại lượng khác nhau theo ẩn.
+ Dựa vào đề bài toán, lập phương trình theo dạng đã học.
– Bước 2: Giải phương trình.
– Bước 3: So sánh kết quả tìm được và chọn nghiệm thích hợp.
8. Tóm tắt các kiến thức cần nhớ
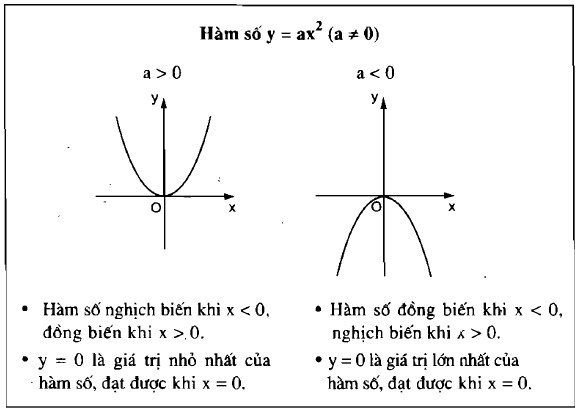

Dưới đây là Hướng dẫn giải bài 54 55 56 57 58 59 60 61 62 63 64 65 66 trang 63 64 sgk toán 9 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập Ôn tập chương IV
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần đại số 9 kèm bài giải chi tiết bài 54 55 56 57 58 59 60 61 62 63 64 65 66 trang 63 64 sgk toán 9 tập 2 của Bài Ôn tập Chương IV – Hàm số \(y = ax^2 (a ≠ 0)\). Phương trình bậc hai một ẩn cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 54 trang 63 sgk Toán 9 tập 2
Vẽ đồ thị của hàm số \(\displaystyle y = {1 \over 4}{x^2}\) và \(\displaystyle y = – {1 \over 4}{x^2}\) trên cùng một hệ trục tọa độ
a) Qua điểm \(B(0; 4)\) kẻ đường thẳng song song với trục Ox. Nó cắt đồ thị của hàm số \(\displaystyle y = {1 \over 4}{x^2}\) tại hai điểm M và M’. Tìm hoành độ của M và M’.
b) Tìm trên đồ thị của hàm số \(\displaystyle y = – {1 \over 4}{x^2}\) điểm N có cùng hoành độ với M, điểm N’ có cùng hoành độ với M’. Đường thẳng NN’ có song song với Ox không? Vì sao? Tìm tung độ của N và N’ bằng hai cách:
– Ước lượng trên hình vẽ:
– Tính toán theo công thức.
Bài giải:
♦ Vẽ đồ thị hàm số: \(\displaystyle y = {1 \over 4}{x^2}\) và \(\displaystyle y = – {1 \over 4}{x^2}\)
– Tập xác định \(D = R\)
– Bảng giá trị:
| $x$ | -4 | -2 | 0 | 2 | 4 |
| y = $\frac{1}{4}$$x^2$ | 4 | 1 | 0 | 1 | 4 |
| y = -$\frac{1}{4}$$x^2$ | -4 | -1 | 0 | -1 | -4 |
– Đồ thị hàm số \(\displaystyle y = {1 \over 4}{x^2}\) và \(\displaystyle y = – {1 \over 4}{x^2}\) là các Parabol có đỉnh là gốc tọa độ O và nhận Oy làm trục đối xứng. Đồ thị hàm số \(\displaystyle y = {1 \over 4}{x^2}\) nằm trên trục hoành, đồ thị hàm số \(\displaystyle y = – {1 \over 4}{x^2}\) nằm dưới trục hoành.

a) Đường thẳng qua \(B(0; 4)\) song song với \(Ox\) có dạng: y = 4.
Phương trình hoành độ giao điểm của đường thẳng y = 4 và đồ thị hàm số \(\displaystyle y = {1 \over 4}{x^2}\) là:
\(\dfrac{1}{4}{x^2} = 4 \Leftrightarrow {x^2} = 16 \Leftrightarrow x = \pm 4\)
Từ đó ta có hoành độ của \(M\) là \(x = 4\), của \(M’\) là \(x = – 4\).
b) Trên đồ thị hàm số \(\displaystyle y = – {1 \over 4}{x^2}\) ta xác định được điểm \(N\) và \(N’\) có cùng hoành độ với \(M, M’\). Ta được đường thẳng \(NN’//Ox\)
Tìm tung độ của \(N, N’\)
– Ước lượng trên hình vẽ được tung độ của \(N\) là \(y = – 4\); của \(N’\) là \(y = -4\)
– Tính toán theo công thức:
Điểm \(N(4;y)\). Thay \(x = 4\) vào \(\displaystyle y = – {1 \over 4}{x^2}\) nên \(\displaystyle y = – {1 \over 4}{.4^2} = – 4\)
Điểm \(N’(-4;y)\). Thay \(x = – 4\) vào \(\displaystyle y = – {1 \over 4}{x^2}\) nên \(\displaystyle y = – {1 \over 4}.{( – 4)^2} = – 4\)
Vậy tung độ của \(N, N’\) cùng bằng \(-4\).
2. Giải bài 55 trang 63 sgk Toán 9 tập 2
Cho phương trình \(x^2 – x – 2 = 0\)
a) Giải phương trình
b) Vẽ hai đồ thị \(y = x^2\) và \(y = x + 2\) trên cùng một hệ trục tọa độ.
c) Chứng tỏ rằng hai nghiệm tìm được trong câu a) là hoành độ giao điểm của hai đồ thị.
Bài giải:
a) Giải phương trình: \(x^2 – x – 2 = 0\)
\(\Delta = (-1)^2– 4.1.(-2) = 1 + 8 > 0\)
\(\sqrt\Delta= \sqrt9 = 3\)
\(\Rightarrow {x_1} = -1; {x_2}= 2\)
b) Vẽ đồ thị hàm số
♦ Hàm số \(y = x^2\)
Bảng giá trị:
| $x$ | -2 | -1 | 0 | 1 | 2 |
| $y = x^2$ | 4 | 1 | 0 | 1 | 4 |
♦ Hàm số \(y = x + 2\)
Cho \(x = 0 ⇒ y = 2\) được điểm \(A(0;2)\)
Cho \(x = -2 ⇒ y = 0\) được điểm \(B(-2;0)\)
Đồ thị hàm số:

c) Ta có phương trình hoành độ giao điểm của hai đồ thị là:
\({x^2} = x + 2 \Leftrightarrow {x^2} – x – 2 = 0\) có \(a – b + c = 1 – \left( { – 1} \right) + \left( { – 2} \right) = 0\) nên có hai nghiệm \({x_1} = – 1;{x_2} = 2.\)
Điều này chứng tỏ rằng đường thẳng cắt đồ thị parapol tại hai điểm có hoành độ lần lượt là \(x = -1; x= 2\). Hai giá trị này cũng chính là nghiệm của phương trình \(x^2 – x – 2 = 0\) ở câu a).
3. Giải bài 56 trang 63 sgk Toán 9 tập 2
Giải các phương trình:
a) \(3{{\rm{x}}^4} – 12{{\rm{x}}^2} + 9 = 0\)
b) \(2{{\rm{x}}^4} + 3{{\rm{x}}^2} – 2 = 0\)
c) \({x^4} + 5{{\rm{x}}^2} + 1 = 0\)
Bài giải:
a) \(3{{\rm{x}}^4} – 12{{\rm{x}}^2} + 9 = 0\)
Đặt \(t = {x^2}\left( {t \ge 0} \right)\)
Ta có phương trình:
\(\eqalign{
& 3{t^2} – 12t + 9 = 0 \cr
& \Leftrightarrow {t^2} – 4t + 3 = 0 \cr} \)
Phương trình có \(a + b + c = 0\) nên có hai nghiệm \({t_1} = 1; {t_2} = 3\) (đều thỏa mãn)
Với \({t_1} = 1 \Rightarrow {x^2} = 1 \Leftrightarrow x = \pm 1\)
Với \({t_2} = 3 \Rightarrow {x^2} = 3 \Leftrightarrow x = \pm \sqrt 3\)
Vậy phương trình đã cho có 4 nghiệm phân biêt.
b) \(2{{\rm{x}}^4} + 3{{\rm{x}}^2} – 2 = 0\)
Đặt \(t = {x^2}\left( {t \ge 0} \right)\)
Ta có phương trình :
\(\eqalign{
& 2{t^2} + 3t – 2 = 0 \cr
& \Delta = 9 + 16 = 25 \Rightarrow \sqrt \Delta = 5 \cr
& \Rightarrow {t_1} = {{ – 3 + 5} \over 4} = {1 \over 2}(TM);{t_2} = – 2(loại) \cr}\)
Với \(\displaystyle t = {1 \over 2} \Rightarrow {x^2} = {1 \over 2} \\\displaystyle \Leftrightarrow x = \pm \sqrt {{1 \over 2}} = \pm {{\sqrt 2 } \over 2}\)
Vậy phương trình đã cho có 2 nghiệm phân biệt.
c) \({x^4} + 5{{\rm{x}}^2} + 1 = 0\)
Đặt \(t = {x^2}\left( {t \ge 0} \right)\)
Ta có phương trình :
\(t^2 + 5t + 1 = 0\)
\(\Delta = 25 – 4 = 21\)
\(\eqalign{
& \Rightarrow {t_1} = {{ – 5 + \sqrt {21} } \over 2} < 0(loại) \cr
& {t_2} = {{ – 5 – \sqrt {21} } \over 2} < 0(loại) \cr} \)
Vậy phương trình vô nghiệm
4. Giải bài 57 trang 63 sgk Toán 9 tập 2
Giải các phương trình:
a) \(5{{\rm{x}}^2} – 3{\rm{x}} + 1 = 2{\rm{x}} + 11\)
b) \(\displaystyle {{{x^2}} \over 5} – {{2{\rm{x}}} \over 3} = {{x + 5} \over 6}\)
c) \(\displaystyle {x \over {x – 2}} = {{10 – 2{\rm{x}}} \over {{x^2} – 2{\rm{x}}}}\)
d) \(\displaystyle {{x + 0,5} \over {3{\rm{x}} + 1}} = {{7{\rm{x}} + 2} \over {9{{\rm{x}}^2} – 1}}\)
e) \(2\sqrt 3 {x^2} + x + 1 = \sqrt 3 \left( {x + 1} \right)\)
f) \({x^2} + 2\sqrt 2 x + 4 = 3\left( {x + \sqrt 2 } \right)\)
Bài giải:
a) Ta có:
\(\eqalign{
& 5{{\rm{x}}^2} – 3{\rm{x}} + 1 = 2{\rm{x}} + 11 \cr
& \Leftrightarrow 5{{\rm{x}}^2} – 5{\rm{x}} – 10 = 0 \cr
& \Leftrightarrow {x^2} – x – 2 = 0 \cr}\)
Phương trình có \(a – b + c = 1 + 1 – 2 = 0\) nên có 2 nghiệm \({x_1}= -1; {x_2}= 2\)
b) Ta có:
\(\eqalign{
& {{{x^2}} \over 5} – {{2{\rm{x}}} \over 3} = {{x + 5} \over 6} \cr
& \Leftrightarrow 6{{\rm{x}}^2} – 20{\rm{x}} = 5{\rm{x}} + 25 \cr
& \Leftrightarrow 6{{\rm{x}}^2} – 25{\rm{x}} – 25 = 0 \cr
& \Delta = {25^2} + 4.6.25 = 1225 \cr
& \sqrt \Delta = 35 \Rightarrow {x_1} = 5;{x_2} = – {5 \over 6} \cr} \)
Vậy phương trình có 2 nghiệm phân biệt \({x_1} = 5;{x_2} = – {5 \over 6}\)
c) \(\displaystyle {x \over {x – 2}} = {{10 – 2{\rm{x}}} \over {{x^2} – 2{\rm{x}}}}\) ĐKXĐ: \(x ≠ 0; x ≠ 2\)
\(\eqalign{
& \Rightarrow {x^2} = 10 – 2{\rm{x}} \cr
& \Leftrightarrow {x^2} + 2{\rm{x}} – 10 = 0 \cr
& \Delta ‘ = 1 + 10 = 11 \cr
& \Rightarrow {x_1} = – 1 + \sqrt {11} (TM) \cr
& {x_2} = – 1 – \sqrt {11} (TM) \cr} \)
Vậy phương trình đã cho có 2 nghiệm phân biệt \({x_1} = – 1 + \sqrt {11},{x_2} = – 1 – \sqrt {11}\)
d) \(\displaystyle {{x + 0,5} \over {3{\rm{x}} + 1}} = {{7{\rm{x}} + 2} \over {9{{\rm{x}}^2} – 1}}\) ĐKXĐ: \(x \ne \pm {1 \over 3}\)
\(\eqalign{
& \Rightarrow {{2{\rm{x}} + 1} \over {3{\rm{x}} + 1}} = {{14{\rm{x}} + 4} \over {9{{\rm{x}}^2} – 1}} \cr
& \Leftrightarrow \left( {2{\rm{x}} + 1} \right)\left( {3{\rm{x}} – 1} \right) = 14{\rm{x}} + 4 \cr
& \Leftrightarrow 6{{\rm{x}}^2} + x – 1 = 14{\rm{x}} + 4 \cr
& \Leftrightarrow 6{{\rm{x}}^2} – 13{\rm{x}} – 5 = 0 \cr
& \Delta = {( – 13)^2} – 4.6.( – 5) = 289 \cr
& \sqrt \Delta = \sqrt {289} = 17 \cr
& \Rightarrow {x_1} = {5 \over 2}(TM) \cr
& {x_2} = – {1 \over 3}(loại) \cr} \)
Vậy phương trình đã cho có 1 nghiệm duy nhất: \(\displaystyle {x_1} = {5 \over 2}\)
e) Ta có:
\(\begin{array}{l}
2\sqrt 3 {x^2} + x + 1 = \sqrt 3 \left( {x + 1} \right)\\
\Leftrightarrow 2\sqrt 3 {x^2} – \left( {\sqrt 3 – 1} \right)x + 1 – \sqrt 3
\end{array}\)
\(\begin{array}{l}
\Delta = {\left( {\sqrt 3 – 1} \right)^2} – 8\sqrt 3 \left( {1 – \sqrt 3 } \right)\\
\Delta = 3 – 2\sqrt 3 + 1 – 8\sqrt 3 + 24\\
= 28 – 10\sqrt 3 \\
= {5^2} – 2.5.\sqrt 3 + {\left( {\sqrt 3 } \right)^2}\\
= {\left( {5 – \sqrt 3 } \right)^2}
\end{array}\)
\(\begin{array}{l}
{x_1} = \dfrac{{\sqrt 3 – 1 – 5 + \sqrt 3 }}{{4\sqrt 3 }} = \dfrac{{1 – \sqrt 3 }}{2}\\
{x_2} = \dfrac{{\sqrt 3 – 1 + 5 – \sqrt 3 }}{{4\sqrt 3 }} = \dfrac{{\sqrt 3 }}{3}
\end{array}\)
Vậy phương trình đã cho có 2 nghiệm phân biệt.
f) Ta có:
\(\eqalign{
& {x^2} + 2\sqrt 2 x + 4 = 3\left( {x + \sqrt 2 } \right) \cr
& \Leftrightarrow {x^2} + \left( {2\sqrt 2 – 3} \right)x + 4 – 3\sqrt 2 = 0 \cr
& \Delta = 8 – 12\sqrt 2 + 9 – 16 + 12\sqrt 2 = 1 \cr
& \sqrt \Delta = 1 \cr
& \Rightarrow {x_1} = {{3 – 2\sqrt 2 + 1} \over 2} = 2 – \sqrt 2 \cr
& {x_2} = {{3 – 2\sqrt 2 – 1} \over 2} = 1 – \sqrt 2 \cr} \)
Vậy phương trình đã cho có 2 nghiệm phân biệt.
5. Giải bài 58 trang 63 sgk Toán 9 tập 2
Giải các phương trình
a) \(1,2{{\rm{x}}^3} – {x^2} – 0,2{\rm{x}} = 0\)
b) \(5{{\rm{x}}^3} – {x^2} – 5{\rm{x}} + 1 = 0\)
Bài giải:
a) \(1,2{{\rm{x}}^3} – {x^2} – 0,2{\rm{x}} = 0\)
\( \Leftrightarrow x\left( {1,2{{\rm{x}}^2} – x – 0,2} \right) = 0\)
\(\Leftrightarrow \left[ \matrix{x = 0 \hfill \cr1,2{{\rm{x}}^2} – x – 0,2 = 0(*) \hfill \cr} \right.\)
Giải (*): \(1,2x^2 – x – 0,2 = 0\)
Ta có: \(a + b + c = 1,2 + (-1) + (-0,2) = 0\)
Vậy (*) có 2 nghiệm: \(\displaystyle {x_1}= 1\); \(\displaystyle {x_2} = {{ – 0,2} \over {1,2}} = – {1 \over 6}\)
Vậy phương trình đã cho có 3 nghiệm: \(\displaystyle {x_1} = 0;{x_2} = 1;{x_3} = – {1 \over 6}\)
b) \(5{{\rm{x}}^3} – {x^2} – 5{\rm{x}} + 1 = 0\)
\(⇔ x^2(5x – 1) – (5x – 1) = 0\)
\(⇔ (5x – 1)(x^2– 1) = 0\)
\( \displaystyle \Leftrightarrow \left[ \matrix{5{\rm{x}} – 1 = 0 \hfill \cr {x^2} – 1 = 0 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{x = \dfrac{1}{5} \hfill \cr x = \pm 1 \hfill \cr} \right.\)
Vậy phương trình đã cho có 3 nghiệm: \(\displaystyle {x_1} = {1 \over 5};{x_2} = – 1;{x_3} = 1\)
6. Giải bài 59 trang 63 sgk Toán 9 tập 2
Giải các phương trình bằng cách đặt ẩn phụ:
a) \(2{\left( {{x^2} – 2{\rm{x}}} \right)^2} + 3\left( {{x^2} – 2{\rm{x}}} \right) + 1 = 0\)
b) \({\left( {x + {1 \over x}} \right)^2} – 4\left( {x + {1 \over x}} \right) + 3 = 0\)
Bài giải:
a) Đặt \({x^2} – 2x = t\), ta thu được phương trình \(2{t^2} + 3t + 1 = 0\)
Phương trình trên có \(a – b + c = 2 – 3 + 1 = 0\) nên có hai nghiệm \(t = – 1;t = – \dfrac{1}{2}.\)
– Với \(t = – 1 \Rightarrow {x^2} – 2x = – 1\\ \Leftrightarrow {x^2} – 2x + 1 = 0\\ \Leftrightarrow {\left( {x – 1} \right)^2} = 0 \Leftrightarrow x = 1\)
– Với \(t = – \dfrac{1}{2} \Rightarrow {x^2} – 2x = – \dfrac{1}{2}\\ \Leftrightarrow {x^2} – 2x + 1 = \dfrac{1}{2} \Leftrightarrow {\left( {x – 1} \right)^2} = \dfrac{1}{2}\)
\( \Leftrightarrow \left[ \begin{array}{l}x – 1 = \dfrac{{\sqrt 2 }}{2}\\x – 1 = – \dfrac{{\sqrt 2 }}{2}\end{array} \right. \\ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{2 + \sqrt 2 }}{2}\\x = \dfrac{{2 – \sqrt 2 }}{2}\end{array} \right.\)
Vậy phương trình đã cho có ba nghiệm \(x = 1;x = \dfrac{{2 + \sqrt 2 }}{2};x = \dfrac{{2 – \sqrt 2 }}{2}\)
b) ĐK: \(x \ne 0.\)
Đặt \(x + \dfrac{1}{x} = t\), ta thu được phương trình \({t^2} – 4t + 3 = 0\)
Phương trình trên có \(a + b + c = 1 + \left( { – 4} \right) + 3 = 0\) nên có hai nghiệm \(t = 1;t = 3.\)
– Với \(t = 1 \Rightarrow x + \dfrac{1}{x} = 1 \Rightarrow {x^2} – x + 1 = 0\) .
Xét \(\Delta = {\left( { – 1} \right)^2} – 4.1.1 = – 3 < 0\) nên phương trình vô nghiệm.
– Với \(t = 3 \Rightarrow x + \dfrac{1}{x} = 3\\ \Rightarrow {x^2} – 3x + 1 = 0\, (*)\)
Phương trình (*) có \(\Delta = {\left( { – 3} \right)^2} – 4.1.1 = 5 > 0\) nên có hai nghiệm \(\left[ \begin{array}{l}x = \dfrac{{3 + \sqrt 5 }}{2}\\x = \dfrac{{3 – \sqrt 5 }}{2}\end{array} \right.\) (thỏa mãn)
Vậy phương trình đã cho có hai nghiệm \(x = \dfrac{{3 + \sqrt 5 }}{2};x = \dfrac{{3 – \sqrt 5 }}{2}\) .
7. Giải bài 60 trang 64 sgk Toán 9 tập 2
Với mỗi phương trình sau, đã biết một nghiệm (ghi kèm theo), hãy tìm nghiệm kia:
a) \(\displaystyle 12{{\rm{x}}^2} – 8{\rm{x}} + 1 = 0;{x_1} = {1 \over 2}\)
b) \(2{{\rm{x}}^2} – 7{\rm{x}} – 39 = 0;{x_1} = – 3\)
c) \({x^2} + x – 2 + \sqrt 2 = 0;{x_1} = – \sqrt 2 \)
d) \({x^2} – 2m{\rm{x}} + m – 1 = 0;{x_1} = 2\)
Bài giải:
a) \(\displaystyle 12{{\rm{x}}^2} – 8{\rm{x}} + 1 = 0;{x_1} = {1 \over 2}\)
Ta có: \(\displaystyle {x_1}{x_2} = {1 \over {12}} \Leftrightarrow {1 \over 2}{x_2} = {1 \over {12}} \Leftrightarrow {x_2} = {1 \over 6}\)
b) \(2{{\rm{x}}^2} – 7{\rm{x}} – 39 = 0;{x_1} = – 3\)
Ta có: \(\displaystyle {x_1}.{x_2} = {{ – 39} \over 2} \Leftrightarrow – 3{{\rm{x}}_2} = {{ – 39} \over 2}\\ \Leftrightarrow \displaystyle {x_2} = {{13} \over 2}\)
c) \({x^2} + x – 2 + \sqrt 2 = 0;{x_1} = – \sqrt 2 \)
Ta có:
\(\eqalign{
& {x_1}.{x_2} = \sqrt 2 – 2 \cr
& \Leftrightarrow – \sqrt 2 .{x_2} = \sqrt 2 – 2 \cr
& \Leftrightarrow {x_2} = {{\sqrt 2 – 2} \over { – \sqrt 2 }} = {{\sqrt 2 \left( {1 – \sqrt 2 } \right)} \over { – \sqrt 2 }} = \sqrt 2 – 1 \cr} \)
d) \({x^2} – 2m{\rm{x}} + m – 1 = 0\, \, (1);{x_1} = 2\)
Vì \({x_1} = 2\) là một nghiệm của pt (1) nên
\(2^2- 2m.2 + m – 1 = 0\)
\(⇔ m = 1\)
Khi \(m = 1\) ta có: \({x_1}{x_2} = m – 1\) (hệ thức Vi-ét)
\(⇔ 2.{x_2}= 0\) (vì \({x_1} = 2\) và \(m = 1\))
\(⇔ {x_2}= 0\)
8. Giải bài 61 trang 64 sgk Toán 9 tập 2
Tìm hai số u và v trong mỗi trường hợp sau:
a) \(u + v = 12\); \(uv = 28\) và \(u > v\)
b) \(u + v = 3; uv = 6\)
Bài giải:
a) \(u + v = 12; uv = 28\) và \(u > v\)
Ta có: \({12^2} – 4.28 = 32 > 0\)
Nên \(u\) và \(v\) là hai nghiệm của phương trình:
\(x^2 – 12x + 28 = 0\)
\(\Delta’= 36 – 28 = 8\)
\( \Rightarrow {x_1} = 6 + 2\sqrt 2 ;{x_2} = 6 – 2\sqrt 2 \)
Vì \(6 + 2\sqrt 2 > 6 – 2\sqrt 2\) nên suy ra \(u = 6 + 2\sqrt 2 ;v = 6 – 2\sqrt 2\)
b) \(u + v = 3; uv = 6\)
Ta có: \({3^2} – 4.6 = – 15 < 0\)
Nên \(u\) và \(v\) không có giá trị nào thỏa mãn đầu bài.
9. Giải bài 62 trang 64 sgk Toán 9 tập 2
Cho phương trình \(7x^2 + 2(m – 1)x – m^2= 0\)
a) Với giá trị nào của \(m\) thì phương trình có nghiệm?
b) Trong trường hợp phương trình có nghiệm, dùng hệ thức Vi-ét, hãy tính tổng các bình phương hai nghiệm của phương trình theo \(m\).
Bài giải:
Xét phương trình \(7x^2 + 2(m – 1)x – m^2 = 0\) (1) có \(a=7\ne 0\)
a) Phương trình (1) có nghiệm khi \(\Delta’ ≥ 0\)
Ta có: \(\Delta’ = (m – 1)^2 – 7(-m^2) = (m – 1)^2 + 7m^2 ≥ 0\) với mọi \(m\)
Vậy phương trình (1) luôn luôn có nghiệm với mọi giá trị của \(m\)
b) Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình (1)
Theo Hệ thức Viet ta có:
\(\left\{ \begin{array}{l}
{x_1} + {x_2} = – \dfrac{2(m-1)}{7}\\
{x_1}.{x_2} = \dfrac{- m^2}{7}
\end{array} \right.\)
Ta có:
\(\begin{array}{l}
x_1^2 + x_2^2=x_1^2 + x_2^2+2x_1x_2-2x_1x_2 \\= {\left( {{x_1} + {x_2}} \right)^2} – 2{x_1}{x_2}\\
= {\left[ {\dfrac{{ – 2\left( {m – 1} \right)}}{7}} \right]^2} – 2.\dfrac{{ – {m^2}}}{7}\\
= \dfrac{{4\left( {{m^2} – 2m + 1} \right)}}{{49}} + \dfrac{{2{m^2}}}{7}\\
= \dfrac{{4{m^2} – 8m + 4 + 14{m^2}}}{{49}}\\
= \dfrac{{18{m^2} – 8m + 4}}{{49}}
\end{array}\)
Vậy \(\displaystyle x_1^2 + x_2^2 = {{18{m^2} – 8m + 4} \over {49}}\) .
10. Giải bài 63 trang 64 sgk Toán 9 tập 2
Sau hai năm, số dân của một thành phố tăng từ \(2 000 000\) người lên \(2 020 050\) người. Hỏi trung bình mỗi năm dân số của thành phố đó tăng bao nhiêu phần trăm?
Bài giải:
Gọi tỉ lệ tăng dân số trung bình mỗi năm là \(x\) % \((x > 0)\).
Sau một năm dân số của thành phố là:
\(\displaystyle 2 000 000 + 2 000 000 . {x \over {100}}= 2 000 000 + 20 000x\) (người)
Sau hai năm, dân số của thành phố là:
\(\displaystyle 2000000 +20 000x + (2000 000 + 20 000x). {x \over {100}}\)
\(= 2000 000 + 40 000x + 200x^2\) (người)
Ta có phương trình:
\(2 000 000 + 40 000x + 200x^2= 2 020 050\)
\(⇔ 4x^2 + 800x – 401 = 0\)
\(\Delta’ = 400^2 – 4(-401) = 160 000 + 1 604\)
\(= 161 604 > 0\)
\(\sqrt\Delta’= \sqrt{161 604} = 402\)
Vậy phương trình có 2 nghiệm:
\(\displaystyle {x_1} = {{ – 400 + 402} \over 4} = 0,5(TM)\)
\(\displaystyle {x_2} = {{ – 400 – 402} \over 4} = – 200,5 < 0\) (loại)
Tỉ lệ tăng dẫn số trung bình hàng năm của thành phố là \(0,5\) %
11. Giải bài 64 trang 64 sgk Toán 9 tập 2
Bài toán yêu cầu tìm tích của một số dương với một số lớn hơn nó 2 đơn vị, nhưng bạn Quân nhầm đầu bài lại tính tích của một số dương với một số bé hơn nó 2 đơn vị. Kết quả của bạn Quân là 120. Hỏi nếu làm đúng đầu bài đã cho thì kết quả phải là bao nhiêu?
Bài giải:
Gọi \(x\) là số dương mà đầu bài cho, \(x >0\)
Bạn Quân đã chọn số \((x – 2)\) để nhân với \(x\).
Theo đề bài, ta có: \(x(x – 2) = 120\) hay \(x^2 – 2x – 120 = 0\)
Phương trình trên có \(\Delta’=(-1)^2-1.(-120)=121>0\)
Suy ra \(x = 1+\sqrt {121}=12\) (thỏa mãn) hoặc \(x=1-\sqrt {121}=-10\) (loại)
Nên số đầu bài cho là \(12\)
Theo đầu bài yêu cầu tìm tích của \(x\) với \(x +2\)
Vậy kết quả đúng phải là: \(12.14 = 168\)
12. Giải bài 65 trang 64 sgk Toán 9 tập 2
Một xe lửa đi từ Hà Nội vào Bình Sơn (Quảng Ngãi). Sau đó 1 giờ, một xe lửa khác đi từ Bình Sơn ra Hà Nội với vận tốc lớn hơn vận tốc của xe lửa thứ nhất là 5km/h. Hai xe gặp nhau tại một ga ở chính giữa quãng đường. Tìm vận tốc của mỗi xe, giả thiết rằng quãng đường Hà Nội – Bình Sơn dài 900km.
Bài giải:
Gọi \(x\) (km/h) là vận tốc của xe lửa thứ nhất. Điều kiện \(x > 0\).
Khi đó vận tốc của xe lửa thứ hai là \(x + 5\) (km/h).
Đến khi gặp nhau tại chính giữa quang đường thì mỗi xe đều đi được \(900:2=450\) km.
Thời gian xe lửa thứ nhất đi từ Hà Nội đến chỗ gặp nhau là: \(\displaystyle {{450} \over x}\) (giờ)
Thời gian xe lửa thứ hai đi từ Bình Sơn đến chỗ gặp nhau là: \(\displaystyle {{450} \over {x + 5}}\) (giờ)
Vì xe lửa thứ hai đi sau \(1\) giờ, nghĩa là thời gian đi đến chỗ gặp nhau ít hơn xe thứ nhất \(1\) giờ. Ta có phương trình:
\(\dfrac{{450}}{x} – \dfrac{{450}}{{x + 5}} = 1\)
\(\begin{array}{l}
\Leftrightarrow 450\left( {x + 5} \right) – 450x = x\left( {x + 5} \right)\\
\Leftrightarrow 450x + 2250 – 450x = {x^2} + 5x\\
\Leftrightarrow {x^2} + 5x – 2250 = 0\\
\Delta = {5^2} – 4.\left( { – 2250} \right) = 9025 > 0,\sqrt \Delta = 95
\end{array}\)
Từ đó ta có: \({x_1} = 45\) (nhận); \({x_2} = -50\) (loại)
Vậy: Vận tốc của xe lửa thứ nhất là \(45\) km/h
Vận tốc của xe lửa thứ hai là \(50\) km/h.
13. Giải bài 66 trang 64 sgk Toán 9 tập 2
Cho tam giác $ABC$ có $BC = 16cm$, đường cao $AH = 12 cm$. Một hình chữ nhật $MNPQ$ có đỉnh $M$ thuộc cạnh $AB$, đỉnh $N$ thuộc cạnh $AC$ còn hai đỉnh $P$ và $Q$ thuộc cạnh $BC$ (h.17). Xác định vị trí của điểm $M$ trên cạnh $AB$ sao cho diện tích của hình chữ nhật đó bằng 36cm2.

Bài giải:
Gọi \(x\) (cm) là độ dài của đoạn \(AK\). Điều kiện \(0 < x < 12\)
Vì \(∆ABC\) đồng dạng \(∆AMN\) nên
\(\eqalign{
& {{MN} \over {BC}} = {{AM} \over {AB}} = {{AK} \over {AH}} = {x \over {12}} \cr
& \Rightarrow MN = {{16x} \over {12}} = {{4{\rm{x}}} \over 3} \cr} \)
Ta có: \(MQ = KH = 12 – x\)
Do đó diện tich hình chữ nhật \(MNPQ\) là: \(\displaystyle \left( {12 – x} \right){{4{\rm{x}}} \over 3}\)
Ta có phương trình:
\(\displaystyle \left( {12 – x} \right){{4{\rm{x}}} \over 3} = 36 \Leftrightarrow {x^2} – 12{\rm{x}} + 27 = 0\)
Phương tình trên có \( \Delta’=(-6)^2-1.27=9>0\)
Suy ra \({x} = 9\) (nhận) hoặc \({x} = 3\) (nhận)
Vậy độ dài của đoạn \(AK = 3cm\) hoặc \(9cm\). Suy ra \( \dfrac {AM}{AB}=\dfrac {1}{4}\) hoặc \( \dfrac {AM}{AB}=\dfrac {3}{4}\)
Khi đó \(M\) sẽ có hai vị trí trên \(AB\) nhưng diện tích hình chữ nhật \(MNPQ\) luôn bằng \(36\) cm2
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 9 khác
- Để học tốt môn Vật lí lớp 9
- Để học tốt môn Sinh học lớp 9
- Để học tốt môn Ngữ văn lớp 9
- Để học tốt môn Lịch sử lớp 9
- Để học tốt môn Địa lí lớp 9
- Để học tốt môn Tiếng Anh lớp 9
- Để học tốt môn Tiếng Anh lớp 9 thí điểm
- Để học tốt môn Tin học lớp 9
- Để học tốt môn GDCD lớp 9
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với giải bài 54 55 56 57 58 59 60 61 62 63 64 65 66 trang 63 64 sgk toán 9 tập 2!
“Bài tập nào khó đã có giaibaisgk.com“
