Hướng dẫn Giải bài 61 62 63 64 trang 91 92 sgk Toán 9 tập 2

Nội Dung

Hướng dẫn giải Bài §8. Đường tròn ngoại tiếp. Đường tròn nội tiếp, Chương III – Góc với đường tròn, sách giáo khoa toán 9 tập hai. Nội dung bài giải bài 61 62 63 64 trang 91 92 sgk toán 9 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 9.

Lý thuyết

1. Định nghĩa

a) Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác và đa giác được gọi là đa giác nội tiếp đường tròn.

b) Đường tròn tiếp xúc với tất cả các cạnh của một đa giác được gọi là đường tròn nội tiếp đa giác và đa giác được gọi là đa giác ngoại tiếp đường tròn.

2. Định lí

Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.

Tâm của hai đường tròn này trùng nhau và được gọi là tâm của đa giác đều

Dưới đây là phần Hướng dẫn trả lời các câu hỏi có trong bài học cho các bạn tham khảo. Các bạn hãy đọc kỹ câu hỏi trước khi trả lời nhé!

Câu hỏi

Trả lời câu hỏi trang 91 sgk Toán 9 tập 2

a) Vẽ đường tròn tâm O bán kính R = 2cm.

b) Vẽ một lục giác đều ABCDEF có tất cả các đỉnh nằm trên đường tròn (O).

c) Vì sao tâm O cách đều các cạnh của lục giác đều ? Gọi khoảng cách này là r.

d) Vẽ đường tròn (O; r).

Trả lời:

a) Vẽ đường tròn tâm O bán kính R = 2cm.

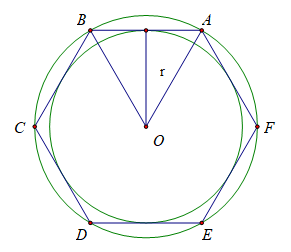
b) Cách vẽ lục giác đều có tất cả các đỉnh nằm trên đường tròn (O)

Vẽ các dây cung AB = BC = CD = DE = EF = FA = R = 2 cm

c) Vì các dây cung AB = BC = CD = DE = EF = FA bằng nhau nên khoảng cách từ O đến các dây là bằng nhau

Dưới đây là Hướng dẫn giải bài 61 62 63 64 trang 91 92 sgk toán 9 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 9 kèm bài giải chi tiết bài 61 62 63 64 trang 91 92 sgk toán 9 tập 2 của Bài §8. Đường tròn ngoại tiếp. Đường tròn nội tiếp trong Chương III – Góc với đường tròn cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 61 62 63 64 trang 91 92 sgk toán 9 tập 2

1. Giải bài 61 trang 91 sgk Toán 9 tập 2

a) Vẽ đường tròn tâm $O$, bán kính $2cm$.

b) Vẽ hình vuông nội tiếp đường tròn $(O)$ ở câu a)

c) Tính bán kính $r$ của đường tròn nội tiếp hình vuông ở câu b) rồi vẽ đường tròn $(O;r)$.

Bài giải:

a) Chọn điểm $O$ làm tâm, mở compa có độ dài $2cm$ vẽ đường tròn tâm $O$, bán kính $2cm$: $(O; 2cm).$

Vẽ bằng eke và thước thẳng.

b) Vẽ đường kính $AC$ và $BD$ vuông góc với nhau. Nối $A$ với $B$, $B$ với $C$, $C$ với $D$, $D$ với $A$ ta được tứ giác $ABCD$ là hình vuông nội tiếp đường tròn $(O;2cm)$

c) Kẻ $OH \bot AD.$

Khi đó ta có $OH$ là bán kính $r$ của đường tròn nội tiếp hình vuông $ABCD$.

Ta có: $\Delta OAD$ là tam giác vuông cân tại $O$ lại có $OH$ là đường cao $\Rightarrow \, H$ là trung điểm của $AB \Rightarrow OH=AH=HB.$

$ \Rightarrow r = OH = AH.$

Áp dụng định lý Pi-ta-go cho tam giác vuông $OHD$ ta có:

$OH^2+AH^2=OA^2$ $\Leftrightarrow {r^2} + {r^2} = {2^2} \Rightarrow 2{r^2} = 4 \Rightarrow r = \sqrt 2 (cm).$

Vẽ đường tròn $(O;\sqrt2cm)$. Đường tròn này nội tiếp hình vuông, tiếp xúc bốn cạnh hình vuông tại các trung điểm của mỗi cạnh.

2. Giải bài 62 trang 91 sgk Toán 9 tập 2

a) Vẽ tam giác $ABC$ cạnh $a = 3cm$.

b) Vẽ đường tròn $(O;R)$ ngoại tiếp tam giác đều $ABC$. Tính $R$.

c) Vẽ đường tròn $(O;r)$ nội tiếp tam giác đều $ABC$. Tính $r$.

d) Vẽ tiếp tam giác đều $IJK$ ngoại tiếp đường tròn $(O;R)$.

Bài giải:

a) Vẽ tam giác đều $ABC$ có cạnh bằng $3cm$ (dùng thước có chia khoảng và compa).

b) Gọi $A’;B’;C’$ lần lượt là trung điểm của $BC;AC;AB.$

Tâm $O$ của đường tròn ngoại tiếp tam giác đều $ABC$ là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác $AA’;BB’;CC’$ của tam giác đều $ABC$).

Tính $AA’$:

Xét tam giác $AA’C$ vuông tại $A’$ có $AC=3;A’C=\dfrac{3}{2}$, theo định lý Pytago ta có $AC^2=AA’^2+A’C^2$$\Rightarrow AA’^2=3^2-\dfrac {3^2}{4}=\dfrac {9}{4} \Rightarrow AA’=\dfrac {3\sqrt {3}}{2}$

Ta có bán kính đường tròn ngoại tiếp tam giác ABC là $R= OA =$ $\dfrac{2}{3}$$AA’$ = $\dfrac{2}{3}$. $\dfrac{3\sqrt{3}}{2}$ = $\sqrt3 (cm)$.

c) Đường tròn nội tiếp $(O;r)$ tiếp xúc ba cạnh của tam giác đều $ABC$ tại các trung điểm $A’, B’, C’$ của các cạnh.

Ta có: $r = OA’ = $$\dfrac{1}{3}$$ AA’$ =$\dfrac{1}{3}$ $\dfrac{3\sqrt{3}}{2}$ = $\dfrac{\sqrt{3}}{2}(cm).$

d) Vẽ các tiếp tuyến với đường tròn $(O;R)$ tại $A,B,C$. Ba tiếp tuyến này cắt nhau tại $I, J, K$. Ta có $∆IJK$ là tam giác đều ngoại tiếp $(O;R)$.

3. Giải bài 63 trang 92 sgk Toán 9 tập 2

Vẽ các hình lục giác đều, hình vuông, hình tam giác đều cùng nội tiếp đường tròn $(O;R)$ rồi tính cạnh của các hình đó theo $R$.

Bài giải:

Để vẽ được hình như bài 63, chúng ta cần xác định độ lớn góc ở tâm, suy ra số đo cung bị chắn.

Vẽ đường tròn (O;R)

Trên đường tròn lấy điểm B sao cho góc AOB bằng 60 độ, lần lượt lấy C, D, E, F cũng tương tự vậy

Ta vẽ được lục giác ABCDEF đều: $\small AB=R$

Ta nhận thấy rằng AD là đường kính của đường tròn, vậy hình vuông sẽ đi qua A và D

Lấy điểm G trên đường tròn sao cho góc AOG bằng 90 độ, lúc đó, góc GOD cũng bằng 90 độ, và góc DOI cũng vậy

Ta vẽ được hình vuông AGDI: $\small AG=R\sqrt{2}$

Trên đường tròn, lấy điểm E sao cho góc COE bằng 120 độ.

Ta vẽ được tam giác ACE đều: $\small AC=R\sqrt{3}$

4. Giải bài 64 trang 92 sgk Toán 9 tập 2

Trên đường tròn bán kính R, lần lượt đặt cùng một chiều, kể từ điểm A, ba cung AB, BC, CD sao cho $\small sd\widehat{AB}=60^o$, $\small sd\widehat{BC}=90^o$ và $\small sd\widehat{CD}=120^o$.

a) Tứ giác ABCD là hình gì?

b) Chứng minh rằng hai đường chéo của tứ giác ABCD vuông góc với nhau.

c) Tính độ dài các cạnh của tứ giác ABCD theo R.

Bài giải:

Với bài tập 64 này, chúng ta sẽ sử dụng tính chất của tứ giác nội tiếp, các tam giác cân, vuông cân,… để giải quyết bài toán

a) Ta có tam giác AOB cân tại O và có góc AOB bằng 60 độ nên:

Tam giác AOB đều

$\Rightarrow \widehat{ABO}=60^o$

Mặc khác, tam giác BOC là tam giác vuông cân:

$\Rightarrow \widehat{OBC}=\widehat{OCB}=45^o$

$\Rightarrow \widehat{ABC}=60^o+45^o=105^o$

Xét tam giác OCD cân tại O có góc COD bằng 120 độ:

$\Rightarrow \widehat{OCD}=30^o$

$\Rightarrow \widehat{BCD}=30^o+45^o=75^o$

Vậy ta có:

$\widehat{BCD}+\widehat{ABC}=75^o+105^o=180^o$

Hai góc này ở vị trí trong cùng phía nên AB//CD

Vậy ABCD là hình thang

Mặc khác tứ giác ABCD là tứ giác nội tiếp nên:

ABCD là hình thang cân! (hình thang nội tiếp đường tròn chắc chắn là hình thang cân)

b) Gọi H là giao điểm của AC và BD

Xét tam giác OAC cân tại O, ta có:

$\widehat{OAC}=\widehat{OCA}=\frac{180^o-150^o}{2}=15^o$

Tương tự đối với tam giác BOD cân tại O, ta có:

$\widehat{OBD}=\widehat{ODB}=\frac{180^o-150^o}{2}=15^o$

$\Rightarrow \widehat{BAH}=\widehat{ABH}=45^o$

Vậy tam giác ABH vuông cân tại H

$\Rightarrow AC\perp BD$

c) Ta có tam giác AOB đều

$\Rightarrow AB=R$

Tam giác OBC và OAD là các tam giác cùng vuông cân tại O

$\Rightarrow BC=AD=R\sqrt{2}$

Tam giác OCD cân tại O có góc ở đình bằng 120 độ

$\Rightarrow CD=R\sqrt{3}$

Bài trước:

Luyện tập: Giải bài 56 57 58 59 60 trang 89 90 sgk Toán 9 tập 2

Bài tiếp theo:

Giải bài 65 66 67 68 69 trang 94 95 sgk Toán 9 tập 2

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với giải bài 61 62 63 64 trang 91 92 sgk toán 9 tập 2!

“Bài tập nào khó đã có giaibaisgk.com“