Luyện tập: Giải bài 56 57 58 59 60 trang 89 90 sgk Toán 9 tập 2

Nội Dung

Luyện tập Bài §7. Tứ giác nội tiếp, Chương III – Góc với đường tròn, sách giáo khoa toán 9 tập hai. Nội dung bài giải bài 56 57 58 59 60 trang 89 90 sgk toán 9 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 9.

Lý thuyết

1. Khái niệm

Một tứ giác có bốn đỉnh cùng nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (hay tứ giác nội tiếp).

2. Định lí

Trong một tứ giác nội tiếp, tổng số đo hai góc đối nhau bằng 180⁰

3. Định lí đảo

Nếu một tứ giác có tổng số đo hai góc đối nhau bằng 180⁰thì tứ giác đó nội tiếp được đường tròn.

Dưới đây là Hướng dẫn giải bài 56 57 58 59 60 trang 89 90 sgk toán 9 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Luyện tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 9 kèm bài giải chi tiết bài 56 57 58 59 60 trang 89 90 sgk toán 9 tập 2 của Bài §7. Tứ giác nội tiếp. Số đo cung trong Chương III – Góc với đường tròn cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 56 57 58 59 60 trang 89 90 sgk toán 9 tập 2

1. Giải bài 56 trang 89 sgk Toán 9 tập 2

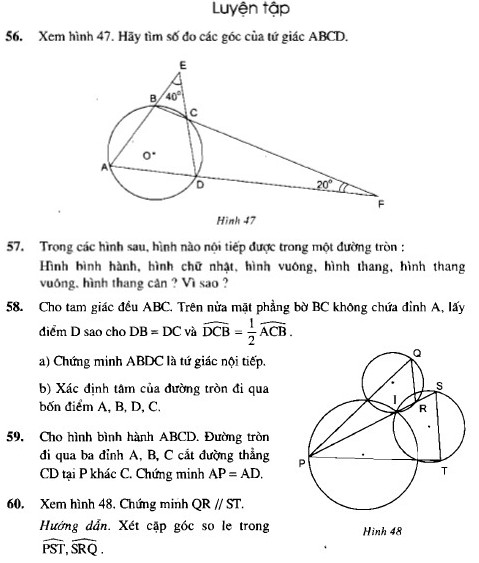
Xem hình 47. Hãy tìm số đo các góc của tứ giác $ABCD.$

Bài giải:

Ta có $\widehat{BCE} = \widehat{DCF}$ (hai góc đối đỉnh)

Đặt $x = \widehat{BCE} = \widehat{DCF}$. Theo tính chất góc ngoài tam giác, ta có:

$\widehat{ABC}= x+40^0$ (góc ngoài của $\Delta BCE$.) (1)

$\widehat{ADC}=x +20^0$ (góc ngoài của $\Delta DCF$.) (2)

Lại có $\widehat{ABC} +\widehat{ADC}=180^0.$ (hai góc đối diện tứ giác nội tiếp). (3)

Từ (1), (2), (3) suy ra: $180^0 =2x + 60^0 \Rightarrow x = 60^0.$

Hay $ \widehat{BCE} = \widehat{DCF}=60^0. $

Từ (1), ta có: $\widehat{ABC}=60^0 +40^0 =100^0.$

Từ (2), ta có: $\widehat{ADC} = 60^0+20^0 = 80^0.$

$\widehat{BCD}= 180^0 – \widehat{BCE} $ (hai góc kề bù)

$\Rightarrow\widehat{BCD} = 120^0$

$\widehat{BAD} = 180^0 – \widehat{BCD}$ (hai góc đối diện của tứ giác nội tiếp)

$\Rightarrow \widehat{BAD}= 180^0– 120^0= 60^0.$

2. Giải bài 57 trang 89 sgk Toán 9 tập 2

Trong các hình sau, hình nào nội tiếp được một đường tròn:

Hình bình hành, hình chữ nhật, hình vuông, hình thang, hình thang vuông, hình thang cân ? Vì sao?

Bài giải:

– Hình bình hành nói chung không nội tiếp được đường tròn vì tổng hai góc đối diện không bằng $180^0$.

– Trường hợp riêng của hình bình hành là hình chữ nhật (hay hình vuông) thì nội tiếp đường tròn vì tổng hai góc đối diện là $90^0 + 90^0= 180^0.$

– Hình thang nói chung và hình thang vuông không nội tiếp được đường tròn, cụ thể đó là tổng hai góc đối chưa chắc bằng 180 độ.

– Hình thang cân $ABCD \, (BC= AD)$ có hai góc ở mỗi đáy bằng nhau: $\widehat{A}= \widehat{B},$ $\widehat{C} =\widehat{D}$

Vì $AD // CD$ nên $\widehat{A} +\widehat{D} = 180^0$ (hai góc trong cùng phía), suy ra $\widehat{A} +\widehat{C} =180^0$.

Vậy hình thang cân luôn có tổng hai góc đối diện bằng $180^0$ nên là tứ giác nội tiếp.

3. Giải bài 58 trang 90 sgk Toán 9 tập 2

Cho tam giác đều $ABC.$ Trên nửa mặt phẳng bờ $BC$ không chứa đỉnh $A,$ lấy điểm $D$ sao cho $DB = DC$ và $\widehat{DCB}=\dfrac{1}{2}\widehat{ACB}.$

a) Chứng minh $ABDC$ là tứ giác nội tiếp.

b) Xác định tâm của đường tròn đi qua bốn điểm $A,\, B,\, D, \,C$.

Bài giải:

a) Theo giả thiết, $\widehat{DCB}=\frac{1}{2}\widehat{ACB} = \dfrac{1}{2} .60^0= 30^0.$

$\widehat{ACD}=\widehat{ACB} +\widehat{BCD}$ (tia $CB$ nằm giữa hai tia $CA,\, CD$)

$\Rightarrow$$\widehat{ACD}=60^0+ 30^0=90^0$ (1)

Do $DB = CD$ nên $∆BDC$ cân tại $D$ $\Rightarrow \widehat{DBC} = \widehat{DCB} = 30^0$

Từ đó $\widehat{ABD}= 30^0+60^0=90^0$ (2)

Từ (1) và (2) có $\widehat{ACD}+ \widehat{ABD}=180^0$ nên tứ giác $ABDC$ là tứ giác nội tiếp.

b) Vì $\widehat{ABD} = 90^0$ nên $AD$ là đường kính của đường tròn ngoại tiếp tứ giác $ABDC,$ do đó tâm đường tròn ngoại tiếp tứ giác $ABDC$ là trung điểm $AD.$

4. Giải bài 59 trang 90 sgk Toán 9 tập 2

Cho hình bình hành $ABCD.$ Đường tròn đi qua ba đỉnh $A, \, B, \, C$ cắt đường thẳng $CD$ tại $P$ khác $C.$ Chứng minh $AP = AD.$

Bài giải:

Do tứ giác $ABCP$ nội tiếp nên ta có:

$\widehat{BAP} + \widehat{BCP} = 180^0.$ (1)

Ta lại có: $\widehat{ABC}+ \widehat{BCP}= 180^0$ (hai góc trong cùng phía do $CD//AB$). (2)

Từ (1) và (2) suy ra: $\widehat{BAP}= \widehat{ABC}.$

Vậy $ABCP$ là hình thang cân, suy ra $AP = BC.$ (3)

Mà $BC = AD$ (hai cạnh đối của hình bình hành) (4)

Từ (3) và (4) suy ra $AP = AD$ (đpcm).

5. Giải bài 60 trang 90 sgk Toán 9 tập 2

Xem hình 48. Chứng minh $QR // ST$.

Bài giải:

Ta có tứ giác ISTM nội tiếp đường tròn nên theo tính chất góc ngoài của tứ giác, ta có: $\widehat{PST}=\widehat{IMP}$

Mặc khác, tứ giác PMIN cũng là tứ giác nội tiếp, theo tính chất góc ngoài, ta có: $\widehat{IMP}=\widehat{INQ}$

Lại sử dụng tính chất góc ngoài đối với tứ giác QSIN nội tiếp trong một đường tròn: $\widehat{INQ}=\widehat{QST}$

Từ các điều trên, ta có thể suy ra: $\widehat{PST}=\widehat{QST}$

Mà hai góc này ở vị trí so le trong nên ta có điều cần chứng minh: $ST//QR$

Bài trước:

Giải bài 53 54 55 trang 89 sgk Toán 9 tập 2

Bài tiếp theo:

Giải bài 61 62 63 64 trang 91 92 sgk Toán 9 tập 2

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với giải bài 56 57 58 59 60 trang 89 90 sgk toán 9 tập 2!

“Bài tập nào khó đã có giaibaisgk.com“