Nội Dung
Luyện tập 1 Bài §18. Bội chung nhỏ nhất, chương I – Ôn tập và bổ túc về số tự nhiên, sách giáo khoa toán 6 tập một. Nội dung bài giải bài 152 153 154 155 trang 59 60 sgk toán 6 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần số học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 6.
Lý thuyết
1. Bội chung
Ví dụ: Nhận xét rằng, các số 0, 6, 12, 18,… vừa là bội của 3 vừa là bội của 6, khi đó ta nói “chúng là bội chung của 3 và 6”.
Từ đó, ta có định nghĩa:
Cho hai số $a$ và $b$. Nếu có một số $d$ thoả mãn: \(d\,\, \vdots \,\,a\) và \(d\,\, \vdots \,\,b\) thì d được gọi là bội chung của $a$ và $b$.
Tập hợp các bội của hai số $a$ và $b$ được kí hiệu là $BC(a, b)$
Chú ý:
Nếu \(x \in BC(a,b,c,…)\) thì \(x\,\, \vdots \,\,a,\,x\,\, \vdots \,\,b,\,x\,\, \vdots \,\,c,…\)
\(BC(a,b) = B(a)\,\, \cap \,\,B(b)\)
2. Bội chung nhỏ nhất
Ví dụ: Ta có
$B(6) = ${$0, 6, 12, 18, 24, 30,…$}
$B(8) = ${$0, 8, 16, 24, 32, 45,…$}
\( \Rightarrow \) BC(6, 8) = {0, 24, 48,…}
Khi đó, số nhỏ nhất khác 0 trong tập hợp $BC(6, 8)$ là $24$. Ta nói $24$ là bội chung nhỏ nhất của $6$ và $8$.
Từ đó, ta có định nghĩa:
Bội chung nhỏ nhất của $a, b$ là số nhỏ nhất khác $0$ trong tập hợp các bội chung của $a, b$. Kí hiệu $BCNN(a, b)$.
Nhận xét:
– $BCNN(a, 1) = a.$
– $BCNN(a, b, 1) = BCNN(a, b).$
– Mọi bội chung của $a$ va $b$ đều là $BCNN(a, b).$
3. Cách tìm BCNN
Bài toán: Tìm $BCNN(a, b, c,…)$
Phương pháp giải:
Ta thực hiện theo ba bước sau:
– Bước 1: Phân tích các số ra thừa số nguyên tố.
– Bước 2: Chọn ra các thừa số chung và riêng.
– Bước 3: Lập tính các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
Chú ý: Ta có thể tìm BCNN bằng cách tính sau:
$ƯCLN(a, b) . BCNN(a,b) = a.b$
Ví dụ: Hãy xác định:
a. BCNN(8,18,28)
b. BCNN(9, 26)
c. BCNN(150, 25, 75)
Bài giải:
Ta lần lượt thực hiện:
– Phân tích các số ra thừa số nguyên tố:
a. Ta có:
\(\begin{array}{l}8 = {2^3}\\18 = {2.3^2}\\28 = {2^2}.7\end{array}\)
– Chọn ra các thừa số nguyên tố chung và riêng: 2, 3, 7.
– Thừa số 2 có số mũ lớn nhất là 3, 3 có số mũ lớn nhất là 2 và 7 có số mũ lớn nhất là 1.
– Khi đó:
\(BCNN\left( {8,{\rm{ }}18,{\rm{ }}28} \right) = {2^3}{.3^2}.7 = 504\)
b. Nhận xét rằng:
ƯCLN(8, 19) = 1
Do đó, suy ra:
BCNN(9, 26) = 9 . 26 = 243.
c. Nhận xét rằng:
\(\begin{array}{l}150\,\,\, \vdots \,\,\,25\\150\,\,\, \vdots \,\,\,75\end{array}\)
Do đó, suy ra:
BCNN(150, 25, 75) = 150
Chú ý:
– Nếu (a, b) = 1 thì BCNN(a, b) = a.b
– Nếu \(a \vdots b\) và \(a \vdots c\) thì BCNN(a,b,c,…)=a.
– Muốn tìm bội chung của các số đã cho ta có thể tìm các bội của BCNN của các số đó.
Dưới đây là Hướng dẫn giải bài 152 153 154 155 trang 59 60 sgk toán 6 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Luyện tập 1
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần số học 6 kèm bài giải chi tiết bài 152 153 154 155 trang 59 60 sgk toán 6 tập 1 của bài §18. Bội chung nhỏ nhất trong chương I – Ôn tập và bổ túc về số tự nhiên cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
1. Giải bài 152 trang 59 sgk Toán 6 tập 1
Tìm số tự nhiên $a$ nhỏ nhất khác $0$, biết rằng $a⋮15$ và $a⋮18$.
Bài giải:
Số tự nhiên $a$ nhỏ nhất khác $0$ chia hết cho cả $15$ và $18$, chính là $BCNN (15, 18)$
Ta có: $15 = 3 . 5$; $18 = 2 . 3^2$
⇒ $BCNN (15, 18) = 2 . 3^2 . 5 = 90$.
Vậy số tự nhiên $a = 90$.
2. Giải bài 153 trang 59 sgk Toán 6 tập 1
Tìm các bội chung nhỏ hơn $500$ của $30$ và $45.$
Bài giải:
Ta có: $30 = 2 . 3 . 5$; $45 = 3^2 . 5$
⇒ $BCNN (30, 45) = 2 . 3^2 . 5 = 90$.
⇒ $BC(90) = ${$90, 180, 270, 360, 450, 540,…$}
Do đó các bội chung nhỏ hơn $500$ của $30$ và $45$ là: $90, 180, 270, 360, 450$.
3. Giải bài 154 trang 59 sgk Toán 6 tập 1
Học sinh lớp $6C$ khi xếp hàng $2$, hàng $3$, hàng $4$, hàng $8$ đều vừa đủ hàng. Biết số học sinh lớp đó trong khoảng từ $35$ đến $60$. Tính số học sinh lớp $6C.$
Bài giải:
Khi học sinh lớp $6C$ xếp hàng $2$, hàng $3$, hàng $4$, hàng $8$ đều đủ hàng có nghĩa là số học sinh lớp $6C$ là bội chung của $2, 3, 4, 8.$
⇒ $BCNN(2, 3, 4, 8) = 2^3 . 3 = 24$.
Ta biết rằng mỗi bội của $24$ cũng là một bội chung của $2, 3, 4, 8$. Nên ta sẽ tìm $BC(24) =$ {$24, 48, 72,…$}
Ở đây số học sinh của lớp $6C$ trong khoảng từ $35$ đến $60$, nên chỉ có $BC(24) = 48$ mới thỏa mãn điều kiện.
Vậy lớp $6C$ có $48$ học sinh.
4. Giải bài 155 trang 60 sgk Toán 6 tập 1
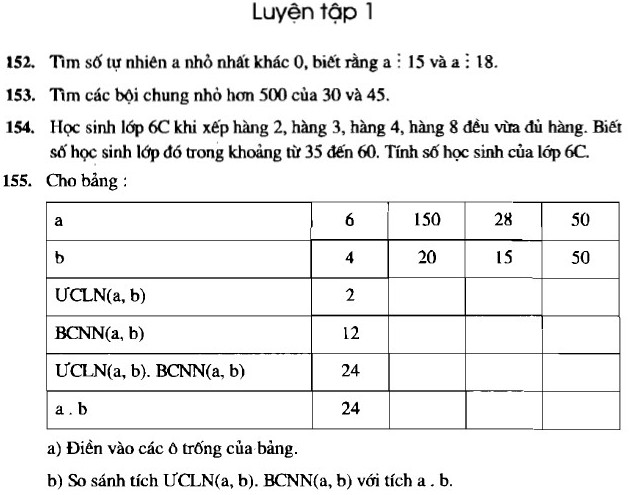
Cho bảng:

a) Điền vào các ô trống của bảng.
b) So sánh tích $ƯCLN (a, b) . BCNN (a, b)$ với tích $a . b$
Bài giải:
a) Ta có:
+) \(150=2.3.5^2\) \(20=2^2.5\)
⇒ \(ƯCLN(a,b)=2.5=10\)
⇒ \(BCNN(a,b)=2^2.3.5^2=300\)
⇒ \(ƯCLN(a,b).BCNN(a,b) = 3000\)
⇒ \(a.b=150.20=3000\)
+) \(28=2^2.7\) \(15=3.5\)
⇒ \(ƯCLN(a,b)=1\)
⇒ \(BCNN(a,b)=2^2.3.5.7=420\)
⇒ \(ƯCLN(a,b).BCNN(a,b) = 420\)
⇒ \(a.b=28.15=420\)
+) \(50=2.5^2\)
⇒ \(ƯCLN(a,b)=50\)
⇒ \(BCNN(a,b)=50\)
⇒ \(ƯCLN(a,b).BCNN(a,b) = 2500\)
⇒ \(a.b=50.50=2500\)
Ta có bảng kết quả:
|
$a$ |
6 |
150 |
28 |
50 |
|
$b$ |
4 |
20 |
15 |
50 |
|
$ƯCLN (a, b)$ |
2 |
10 |
1 |
50 |
|
$BCNN (a, b)$ |
12 |
300 |
420 |
50 |
|
$ƯCLN(a, b) . BCNN (a, b)$ |
24 |
3000 |
420 |
2500 |
|
$a . b$ |
24 |
3000 |
420 |
2500 |
b) Từ kết quả của bảng trên ta có:
$ƯCLN (a, b) . BCNN (a, b) = a . b$
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 6 khác
- Để học tốt môn Vật lí lớp 6
- Để học tốt môn Sinh học lớp 6
- Để học tốt môn Ngữ văn lớp 6
- Để học tốt môn Lịch sử lớp 6
- Để học tốt môn Địa lí lớp 6
- Để học tốt môn Tiếng Anh lớp 6
- Để học tốt môn Tiếng Anh lớp 6 thí điểm
- Để học tốt môn Tin học lớp 6
- Để học tốt môn GDCD lớp 6
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 6 với giải bài 152 153 154 155 trang 59 60 sgk toán 6 tập 1!
“Bài tập nào khó đã có giaibaisgk.com“
