Luyện tập: Giải bài 35 36 37 trang 126 sgk Toán 9 tập 2

Nội Dung

Luyện tập Bài §3. Hình cầu. Diện tích hình cầu và thể tích hình cầu, Chương IV – Hình trụ – Hình nón – Hình cầu, sách giáo khoa toán 9 tập hai. Nội dung bài giải bài 35 36 37 trang 126 sgk toán 9 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 9.

Lý thuyết

1. Hình cầu

Khi quay nửa đường tròn tâm O, bán kính R một vòng quanh đường kính AB cố định, ta được một hình cầu.

2. Cắt hình cầu bởi một mặt phẳng

Bất cứ một mặt phẳng nào cắt qua mặt cầu, ta đều nhận được mặt cắt là hình tròn

Bất cứ một mặt phẳng nào cắt qua tâm mặt cầu, ta đều nhận được mặt cắt là hình tròn có diện tích lớn nhất (vì bán kính lớn nhất)

3. Diện tích mặt cầu

Nhắc lại kiến thức đã học ở lớp dưới, ta có công thức sau:

$S=4\pi R^2=\pi d^2$ (với R là bán kính, d là đường kính của mặt cầu)

4. Thể tích mặt cầu

Công thức tính thể tích mặt cầu:

$V=\frac{4}{3}\pi R^3$

Dưới đây là Hướng dẫn giải bài 35 36 37 trang 126 sgk toán 9 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Luyện tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 9 kèm bài giải chi tiết bài 35 36 37 trang 126 sgk toán 9 tập 2 của Bài §3. Hình cầu. Diện tích hình cầu và thể tích hình cầu trong Chương IV – Hình trụ – Hình nón – Hình cầu cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 35 36 37 trang 126 sgk toán 9 tập 2

1. Giải bài 35 trang 126 sgk Toán 9 tập 2

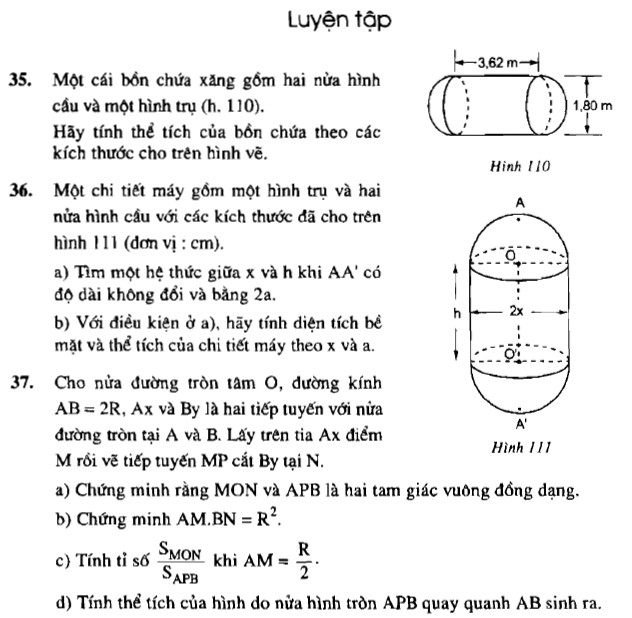
Một cái bồn chứa xăng gồm hai cửa hình cầu và hình trụ (h110)

Hãy tính thể tích của bồn chưa theo kích thước cho trên hình vẽ.

Bài giải:

Thể tích cần tính gồm thể tích một hình trụ và thể tích một hình cầu với:

– Bán kính đáy của hình trụ là $0,9m$, chiều cao là $3,62m$.

– Bán kính của hình cầu là $0,9 m$

Thể tích của hình trụ là:

${V_{trụ}} = {\rm{ }}\pi {r^2}h{\rm{ }} = {\rm{ }}3,14{\rm{ }}{\left( {0,9} \right)^2}.3,62 = 9,215{\rm{ }}({m^3})$

Thể tích của hình cầu là:

${V_{cầu}} = {4 \over 3}\pi {R^3} = {4 \over 3}.3,14.{(0,9)^3} = 3,055({m^3})$

Thể tích của bồn chứa xăng:

$V = {V_{trụ}} + {\rm{ }}{V_{cầu}} = {\rm{ }}9,215{\rm{ }} + {\rm{ }}3,055{\rm{ }} = {\rm{ }}12,27({m^3})$

2. Giải bài 36 trang 126 sgk Toán 9 tập 2

Một chi tiết máy gồm một hình trù và hai nửa hình cầu với các kích thước đã cho trên hình 111 (đơn vị: cm)

a) Tìm một hệ thức giữa $x$ và $h$ khi $AA’$ có độ dài không đổi và bằng $2a$.

b) Với điều kiện ở a) hãy tính diện tích bề mặt và thể tích của chi tiết theo $x$ và $a$.

Bài giải:

a) Từ hình 111, ta thấy đường kính của 2 nửa hình cầu là $2x$ ⇒ bán kính mỗi nửa cầu là $x$.

Do đó: $AA’=OA +OO’+O’A’=x+h+x=2x+h$

⇒ $2a=2x+h$

b) Diện tích cần tính gồm diện tích xung quanh của hình trụ có bán kính đáy là $x$, chiều cao là $h$ và diện tích mặt cầu có bán kính là $x$.

Diện tích xung quanh của hình trụ: ${S_{trụ}} = {\rm{ }}2\pi xh$

Diện tích mặt cầu:${S_{cầu}} = {\rm{ }}4\pi {x^2}$

Diện tích bề mặt của chi tiết máy là:

$S{\rm{ }} = {\rm{ }}{S_{trụ}} + {S_{cầu}}$

$= 2\pi xh{\rm{ }} + 4\pi {x^{2}} = 2\pi x\left( {h + 2x} \right){\rm{ }} = {\rm{ }}4\pi ax$

Thể tích cần tìm gồm thể tích hình trụ và thể tích hình cầu. Ta có:

${V_{trụ}}{\rm{ }} = \pi {x^2}h$

${V_{cầu}} = {4 \over 3}\pi {x^3}$

Nên thể tích của chi tiết máy là:

$V = {V_{trụ}} + {V_{cầu}} = \pi {x^2}h + {4 \over 3}\pi {x^3}$

$= 2\pi {x^2}(a – x) + {4 \over 3}\pi {x^3} = 2\pi {x^2}\left( {a – {1 \over 3}x} \right)$

3. Giải bài 37 trang 126 sgk Toán 9 tập 2

Cho nửa đường tròn tâm $O$, đường kính $AB = 2R$, $Ax$ và $By$ là hai tiếp tuyến với nửa đường tròn tại $A$ và $B$. Lấy trên tia $Ax$ điểm $M$ rồi vẽ tiếp tuyến $MP$ cắt $By$ tại $N$.

a) Chứng minh rằng $MON$ và $APB$ là hai tam giác vuông đồng dạng.

b) Chứng minh rằng $AM.BN = R^2$

c) Tính tỉ số $\frac{S_{MON}}{S_{APB}}$khi $AM$ = $\frac{R}{2}$

d) Tính thể tích của hình do nửa hình tròn $APB$ quay quanh $AB$ sinh ra.

Bài giải:

a) Ta có $OM$, $ON$ lần lượt là tia phân giác của $\widehat {AOP}$ và $\widehat {BOP}$ (tính chất hai tiếp tuyến cắt nhau)

Mà $\widehat {AOP}$ kề bù $\widehat {BOP}$ nên suy ra $OM$ vuông góc với $ON$. (tính chất 2 tiếp tuyến của hai góc kề bù thì vuông góc với nhau)

Vậy $∆MON$ vuông tại $O$ ⇒ $\widehat{MON}=90^{\circ}$

Ta có: Tứ giác $AOPM$ nội tiếp một đường tròn vì có $\widehat{MAP}$ + $\widehat{MPO}$ = $180^0$ (2 góc vuông do Ax và MP là 2 tiếp tuyến của (O) tại A và P).

⇒ $\widehat{PMO}$ = $\widehat{PAO}$ (cùng chắn cung $OP$ trong đường tròn đường kính OM).

Xét hai tam giác $MON$ và $APB$ có:

$\widehat{MON}=\widehat{APB} (=90^{\circ})$

$\widehat{PMO}$ = $\widehat{PAO}$ (cmt)

⇒ $\Delta MON \sim \Delta APB $ (g.g)

b)Ta có: $AM = MP, BN = NP$ (1) (tính chất hai tiếp tuyến cắt nhau)

Tam giác vuông $MON$ có $OP$ là đường cao nên: $MP.PN = OP^2$ (Hệ thúc lượng trong tam giác vuông) (2)

Từ (1) và (2) suy ra $AM.BN = {OP^2} = {R^2}$

c) Ta có: $\Delta MON \sim \Delta APB$ (cmt)

⇒ $\frac{MN}{AB}=\frac{OM}{AP}=\frac{ON}{PB}$ (các cạnh tương ứng tỉ lệ) (3)

Ta có: $S_{MON}=\frac{1}{2}.OM.ON$

$S_{APN}=\frac{1}{2}.AP.PB$

⇒ $\frac{S_{MON}}{S_{APN}}=\frac{OM.ON}{AP.PB}=\frac{OM}{AP}.\frac{ON}{PB}$

Thay (3) vào ta có: $\frac{S_{MON}}{S_{APN}}=(\frac{MN}{AB})^{2}=\frac{MN^{2}}{AB^{2}}$

Khi $AM$ = $\frac{R}{2}$ thì từ $AM.BN = {R^{2{\rm{ }}}}$ suy ra $BN = 2R$

Do đó $MN = MP + PN = AM + BN$ = $\frac{R}{2}$ + $2R$ = $\frac{5R}{2}$

Suy ra $MN^2$ = $\frac{25R^2}{4}$

Vậy $\frac{S_{MON}}{S_{APB}}$ = $\frac{ \frac{25R^2}{4}}{(2R)^2}= \frac{25}{16}$

d) Nửa hình tròn $APB$ quay quanh đường kính $AB = 2R$ sinh ra một hình cầu có bán kính $R$.

Vậy thể tích hình câu được sinh ra là: $V$ = $\frac{4}{3}$$πR^3$

Bài trước:

Giải bài 30 31 32 33 34 trang 124 125 sgk Toán 9 tập 2

Bài tiếp theo:

Trả lời câu hỏi 1 2 trang 128 sgk Toán 9 tập 2

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 9 với giải bài 35 36 37 trang 126 sgk toán 9 tập 2!

“Bài tập nào khó đã có giaibaisgk.com“