Nội Dung
Luyện tập Bài §6. Tam giác cân, chương II – Tam giác, sách giáo khoa toán 7 tập một. Nội dung bài giải bài 50 51 52 trang 127 128 sgk toán 7 tập 1 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 7.
Lý thuyết
1. Định nghĩa
Tam giác cân là tam giác có hai cạnh bằng nhau.
2. Tính chất
– Trong một tam giác cân hai góc ở đáy bằng nhau.
– Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân
– Tam giác vuông cân là tam giác vuông hai cạnh góc vuông bằng nhau.
3. Tam giác đều
Định nghĩa: Tam giác đều là tam giác có ba cạnh bằng nhau.
Hệ quả:
– Trong tam giác đều, mỗi góc bằng \({60^0}\)
– Nếu một tam giác có ba góc bằng nhau thì tam giác đó là tam giác đều.
– Nếu một tam giác cân có một góc bằng \({60^0}\) thì tam giác đó là tam giác đều.
Dưới đây là Hướng dẫn giải bài 50 51 52 trang 127 128 sgk toán 7 tập 1. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Luyện tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần hình học 7 kèm bài giải chi tiết bài 50 51 52 trang 127 128 sgk toán 7 tập 1 của bài §6. Tam giác cân trong chương II – Tam giác cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:
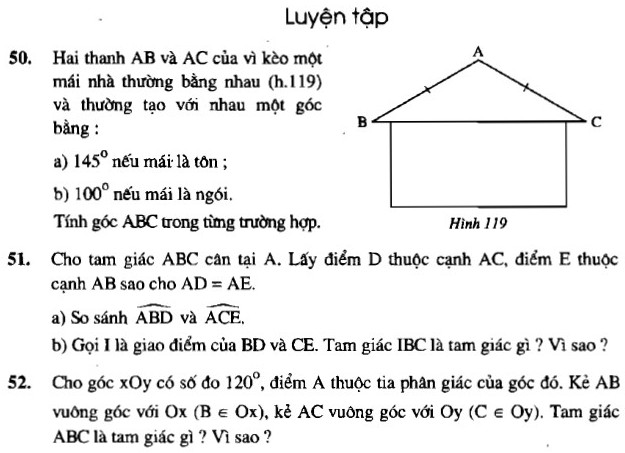
1. Giải bài 50 trang 127 sgk Toán 7 tập 1
Hai thanh AB và AC của vỉ kèo một mái nhà thường bằng nhau (h.119) và thường tạo với nhau một góc bằng:
a) $145^0$ nếu mái là tôn.
b) $100^0$ nếu mái là ngói.
Tính góc $ABC$ trong từng trường hợp.

Bài giải:
a) Ta có $AB = AC$ nên tam giác $ABC$ cân tại $A$.
Khi đó $\widehat{A}$ = $145^0$
Suy ra $\widehat{B}$ = $\widehat{C}$
Trong tam giác $ABC$ có:
$\widehat{B}$ + $\widehat{B}$ + $\widehat{C}$ = $180^0$ (định lí tổng ba góc của một tam giác)
Hay $\widehat{A}$ + 2$\widehat{B}$ = $180^0$
⇒ 2$\widehat{B}$ = $180^0$ – $\widehat{A}$ = $180^0$ – $145^0$ = $35^0$.
⇒ $\widehat{B}$ = $17,5^0$.
Vậy $\widehat{B}$ = $\widehat{C}$ = $17,5^0$.
b) Tương tự, ta cũng có tam giác $ABC$ cân tại $A$, $\widehat{B}$ = $\widehat{C}$.
Nhưng lúc này $\widehat{A}$ = $100^0$.
Nên 2$\widehat{B}$ = $180^0$ – $\widehat{A}$ = $180^0$ – $100^0$ = $80^0$.
⇒ $\widehat{B}$ = $40^0$.
Vậy $\widehat{B}$ = $\widehat{C}$ = $40^0$.
2. Giải bài 51 trang 128 sgk Toán 7 tập 1
Cho tam giác $ABC$ cân tại $A$. Lấy điểm $D$ thuộc cạnh $AC$, điểm $E$ thuộc cạnh $AB$ sao cho $AD = AE$.
a) So sánh $\widehat{ABD}$ và $\widehat{ACE}$.
b) Gọi $I$ là giao điểm của $BD$ và $CE$. Tam giác $IBC$ là tam giác gì? Vì sao?
Bài giải:


a) Xét hai tam giác $ADB$ và $AEC$ có:
$AB = AC$ (vì tam giác ABC cân tại A).
$\widehat{A}$ chung.
$AD = AE (gt)$
Vậy $\Delta ADB = \Delta AEC (c-g-c)$
Suy ra $\widehat{ABD}$ = $\widehat{ACE}$.
b) Ta có
$\widehat{DBC}$ = $\widehat{ABC}$ – $\widehat{ABD}$ (1)
$\widehat{ECB}$ = $\widehat{ACB}$ – $\widehat{ACE}$ (2)
Mà $\widehat{ABC}$ = $\widehat{ACB}$ (tam giác ABC cân tại A) (3)
$\widehat{ABD}$ = $\widehat{ACE}$ (cmt) (4)
Từ (1), (2), (3), (4) suy ra $\widehat{DBC}$ = $\widehat{ECB}$.
Do đó tam giác $IBC$ cân tại $I$.
3. Giải bài 52 trang 128 sgk Toán 7 tập 1
Cho góc $xOy$ có số đo $120^0$, điểm $A$ thuộc tia phân giác của góc đó. Kẻ $AB$ vuông góc với $Ox$ (B $\in$ Ox), kẻ $AC$ vuông góc với $Oy$ (C $\in$ Oy). Tam giác $ABC$ là tam giác gì? Vì sao?
Bài giải:

Ta có:
$\widehat{A_1}$ = $90^0$ – $\widehat{O_1}$ (hai góc phụ nhau)
$\widehat{A_2}$ = $90^0$ – $\widehat{O_2}$ (hai góc phụ nhau)
Mà $\widehat{O_1}$ = $\widehat{O_2}$ (OA là tia phân giác $\widehat{xOy}$)
Nên $\widehat{A_1}$ = $\widehat{A_2}$.
Xét hai tam giác $AOB$ và $AOC$ có:
$\widehat{A_1}$ = $\widehat{A_2}$ (cmt)
Cạnh $OA$ chung.
$\widehat{O_1}$ = $\widehat{O_2}$ (OA là tia phân giác $\widehat{xOy}$)
Vậy $\Delta$ AOB = $\Delta$ AOC (g-c-g)
Suy ra $AB = AC$.
Do đó tam giác $ABC$ cân. (1)
Ta có:
$\widehat{A_1}$ = $90^0$ – $\widehat{O_1}$ = $90^0$ – $\frac{\widehat{O}}{2}$
= $90^0$ – $\frac{\widehat{120^0}}{2}$ = $30^0$
$\widehat{A_2}$ = $90^0$ – $\widehat{O_2}$ = $90^0$ – $\frac{\widehat{O}}{2}$
= $90^0$ – $\frac{\widehat{120^0}}{2}$ = $30^0$
⇒ $\widehat{A}$ = $\widehat{A_1}$ + $\widehat{A_2}$
= $30^0$ + $30^0$ = $60^0$ (2)
Từ (1) và (2) suy ra tam giác $ABC$ là tam giác đều.
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 7 khác
- Để học tốt môn Vật lí lớp 7
- Để học tốt môn Sinh học lớp 7
- Để học tốt môn Ngữ văn lớp 7
- Để học tốt môn Lịch sử lớp 7
- Để học tốt môn Địa lí lớp 7
- Để học tốt môn Tiếng Anh lớp 7
- Để học tốt môn Tiếng Anh lớp 7 thí điểm
- Để học tốt môn Tin học lớp 7
- Để học tốt môn GDCD lớp 7
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 7 với giải bài 50 51 52 trang 127 128 sgk toán 7 tập 1!
“Bài tập nào khó đã có giaibaisgk.com“
