Nội Dung
Hướng dẫn giải Bài Ôn tập chương III – Tam giác đồng dạng, sách giáo khoa toán 8 tập hai. Nội dung bài giải bài 56 57 58 59 60 61 trang 92 sgk toán 8 tập 2 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần hình học có trong SGK toán để giúp các em học sinh học tốt môn toán lớp 8.
Lý thuyết
1. Đoạn thẳng tỉ lệ
a) Định nghĩa
AB, CD tỉ lệ với A’B’, C’D’ $\Leftrightarrow \frac{AB}{CD}=\frac{A’B’}{C’D’}$.
b) Tính chất
$\frac{{AB}}{{CD}} = \frac{{A’B’}}{{C’D’}} \Leftrightarrow \left\{ \begin{array}{l}AB.C’D’ = A’B’.CD\\\frac{{AB \pm CD}}{{CD}} = \frac{{A’B’ \pm C’D’}}{{C’D’}}\\\frac{{AB}}{{CD}} = \frac{{A’B’}}{{C’D’}} = \frac{{AB \pm A’B’}}{{CD \pm C’D’}}\end{array} \right.$
2. Định lí Ta-lét thuận và đảo
Cho tam giác ABC (h.61)
${\rm{a//BC}} \Rightarrow \left[ \begin{array}{l}\frac{{{\rm{AB’}}}}{{{\rm{AB}}}}{\rm{ = }}\frac{{{\rm{AC’}}}}{{{\rm{AC}}}}\\\frac{{{\rm{AB’}}}}{{{\rm{BB’}}}}{\rm{ = }}\frac{{{\rm{AC’}}}}{{{\rm{CC’}}}}\\\frac{{{\rm{BB’}}}}{{{\rm{AB}}}}{\rm{ = }}\frac{{{\rm{CC’}}}}{{{\rm{AC}}}}\end{array} \right.$

3. Hệ quả của định lí Ta-lét
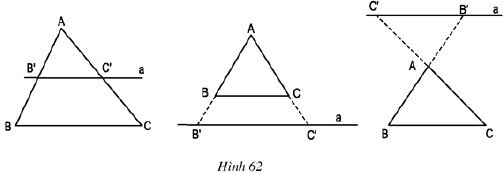
Cho tam giác ABC
$a//BC \Rightarrow \frac{AB’}{AB}=\frac{AC’}{AC}=\frac{B’C’}{BC}$
4. Tính chất của đường phân giác trong tam giác
AD là tia phân giác của góc BAC, AE là tia phân giác của góc BAx (h. 63)
Ta có: $\frac{AB}{AC}=\frac{DB}{DC}=\frac{EB}{EC}$

5. Tam giác đồng dạng
a) Định nghĩa
$\Delta A’B’C’ \sim \Delta ABC$ (tỉ số đồng dạng k)
$\Leftrightarrow \left\{ \begin{array}{l}\widehat {{\rm{A’}}}{\rm{ = }}\widehat {\rm{A}}{\rm{;}}\widehat {{\rm{B’}}}{\rm{ = }}\widehat {\rm{B}}{\rm{;}}\widehat {{\rm{C’}}}{\rm{ = }}\widehat {\rm{C}}\\\frac{{A’B’}}{{AB}} = \frac{{B’C’}}{{BC}} = \frac{{C’A’}}{{CA}} = k\end{array} \right.$
b) Tính chất

$\frac{h}{h’}=k$ (h’; h tương ứng là đường cao của tam giác A’B’C’ và tam giác ABC)
$\frac{p’}{p}=k;\,\ \frac{S’}{S}=k^2$ (p’; p tương ứng là chu vi của tam giác A’B’C’ và tam giác ABC; S’, S tương ứng là diện tích của tam giác A’B’C’ và tam giác ABC)
6. Liên hệ giữa các trường hợp đồng dạng và các trường hợp bằng nhau của hai tam giác ABC và A’B’C’

7. Các trường hợp đồng dạng của hai tam giác vuông ABC và A’B’C’ ($\widehat{A’}=\widehat{A}=90^0$)

a) $\frac{{A’B’}}{{AB}} = \frac{{A’C’}}{{AC}}\Rightarrow \Delta A’B’C’ \sim \Delta ABC$
b) $\widehat{B’}=\widehat{B}\Rightarrow \Delta A’B’C’ \sim \Delta ABC$ hoặc $\widehat{C’}=\widehat{C}\Rightarrow \Delta A’B’C’ \sim \Delta ABC$
c) $\frac{{A’B’}}{{AB}} = \frac{{B’C’}}{{BC}}\Rightarrow \Delta A’B’C’ \sim \Delta ABC$
Dưới đây là Hướng dẫn giải bài 56 57 58 59 60 61 trang 92 sgk toán 8 tập 2. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần đại số 8 kèm bài giải chi tiết bài 56 57 58 59 60 61 trang 92 sgk toán 8 tập 2 của Bài Ôn tập chương III – Tam giác đồng dạng cho các bạn tham khảo. Nội dung chi tiết câu trả lời từng câu hỏi các bạn xem dưới đây:

1. Giải bài 56 trang 92 sgk Toán 8 tập 2
Xác định tỉ số của hai đoạn thẳng \(AB\) và \(DC\) trong các trường hợp sau:
a) \(AB = 5cm, CD = 15 cm;\)
b) \(AB = 45 dm, CD = 150 cm;\)
c) \(AB = 5CD.\)
Bài giải:
a) \(AB = 5cm\) và \(CD = 15cm\)
\( \Rightarrow \dfrac{{AB}}{{CD}} = \dfrac{5}{{15}} = \dfrac{1}{3}\)
b) \(AB = 45dm = 450cm\) và \(CD = 150 cm\)
\( \Rightarrow \dfrac{{AB}}{{CD}} = \dfrac{{450}}{{150}} = 3\)
c) \(AB = 5CD\) \( \Rightarrow \dfrac{{AB}}{{CD}} = \dfrac{{5CD}}{{CD}} = 5\)
2. Giải bài 57 trang 92 sgk Toán 8 tập 2
Cho tam giác \(ABC (AB < AC)\). Vẽ đường cao \(AH\), đường phân giác \(AD\), đường trung tuyến \(AM\). Có nhận xét gì về vị trí của ba điểm \(H, D, M\).
Bài giải:

Nhận xét: \(D\) luôn nằm giữa \(H\) và \(M\).
Chứng minh:
\(AD\) là đường phân giác của \(∆ABC\).
\(\Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{DB}}{{DC}}\) (tính chất đường phân giác của tam giác)
Mà \(AB < AC\) (giả thiết)
\( \Rightarrow DB < DC\) \( \Rightarrow DB + DC < DC + DC\)
\( \Rightarrow BD + DC < 2DC\) hay \(BC < 2DC\)
\( \Rightarrow DC >\dfrac{{BC}}{2}\)
Mà \(MC = \dfrac{{BC}}{2}\) (\(M\) là trung điểm của \(BC\))
\( \Rightarrow DC > MC\) \( \Rightarrow M \) nằm giữa \(D\) và \(C\) (1)
Mặt khác: \(\widehat {CAH} = {90^0} – \hat C\) (\(∆CAH\) vuông tại \(H\))
\(\hat A + \hat B + \hat C = {180^0}\) (tổng 3 góc ∆ABC)
\( \Rightarrow \widehat {CAH} = \dfrac{{\widehat A + \widehat B + \widehat C}}{2} – \widehat C\)
\( \Rightarrow \widehat {CAH} = \dfrac{{\widehat A}}{2} + \dfrac{{\widehat B}}{2} – \dfrac{{\widehat C}}{2}\)\(\, = \dfrac{{\widehat A}}{2} + \dfrac{{\widehat B – \widehat C}}{2}\)
Vì \(AB < AC\) \( \Rightarrow \widehat C < \widehat B \Rightarrow \widehat B – \widehat C > 0\)
Do đó: \(\widehat {CAH} > \dfrac{{\widehat A}}{2}\) hay \(\widehat {CAH} > \widehat {CAD}\)
\( \Rightarrow \) Tia \(AD\) nằm giữa hai tia \(AH\) và \(AC\)
Do đó \(D\) nằm giữa hai điểm \(H\) và \(C\) (2)
Từ (1) và (2) suy ra \(D\) nằm giữa \(H\) và \(M.\)
3. Giải bài 58 trang 92 sgk Toán 8 tập 2
Cho tam giác cân \(ABC (AB = AC)\), vẽ các đường cao \(BH, CK\) (H.66).
a) Chứng minh \(BK = CH\).
b) Chứng minh \(KH//BC\).
c) Cho biết \(BC = a, AB = AC = b\). Tính độ dài đoạn thẳng \(HK\).
Hướng dẫn câu c):
– Vẽ thêm đường cao \(AI\), xét hai tam giác đồng dạng \(IAC\) và \(HBC\) rồi tính \(CH\).
– Tiếp theo, xét hai tam giác đồng dạng \(AKH\) và \(ABC\) rồi tính \(HK\).

Bài giải:

a) Xét hai tam giác vuông \(BKC\) và \(CHB\) có:
\(\widehat {KBC} = \widehat {HCB}\) (\(∆ABC\) cân tại \(A\))
\(BC\) là cạnh chung
\( \Rightarrow ∆BKC = ∆CHB\) (cạnh huyền – góc nhọn)
\( \Rightarrow BK = CH\) (2 cạnh tương ứng)
b) Ta có : \(AK = AB – BK, AH = AC – HC\) (gt)
Mà \(AB = AC\) (\(∆ABC\) cân tại \(A\))
\(BK = CH\) (chứng minh trên)
\( \Rightarrow AK = AH\)
Do đó : \(\dfrac{{AK}}{{AB}} = \dfrac{{AH}}{{AC}}\) \( \Rightarrow KH // BC\) (định lí Ta lét đảo)
c) \(BH\) cắt \(CK\) tại \(M\)
\( \Rightarrow M\) là trực tâm của \(∆ABC\) (định nghĩa trực tâm)
\( \Rightarrow AM ⊥ BC\) tại \(I\) (tính chất trực tâm)
Ta có : \(∆AIC ∽ ∆BHC \,(g-g)\) vì \(\left\{ {\matrix{{\widehat I = \widehat H = {{90}^0}} \cr {\widehat C\;chung} \cr} } \right.\)
\( \Rightarrow \dfrac{{IC}}{{HC}} = \dfrac{{AC}}{{BC}}\) (tính chất hai tam giác đồng dạng)
hay \({{{a \over 2}} \over {HC}} = {b \over a} ⇒ HC = {{{a^2}} \over {2b}}\)
⇒ \(AH = b – {{{a^2}} \over {2b}} = {{2{b^2} – {a^2}} \over {2b}}\)
Mà HK // BC ⇒ \({{HK} \over {BC}} = {{AH} \over {AC}} ⇒ HK = {{BC.AH} \over {AC}}\)
⇒ \(HK = {a \over b}\left( {{{2{b^2} – {a^2}} \over {2b}}} \right) = {{2a{b^2} – {a^2}} \over {2{b^2}}}\)
4. Giải bài 59 trang 92 sgk Toán 8 tập 2
Hình thang \(ABCD \,(AB//CD)\) có \(AC\) và \(BD\) cắt nhau tại \(O, AD\) và \(BC\) cắt nhau tại \(K\). Chứng minh rằng \(OK\) đi qua trung điểm của các cạnh \(AB\) và \(CD\).
Bài giải:

Qua \(O\) kẻ đường thẳng song song với \(AB, CD\) cắt \(AD, BC\) lần lượt tại \(E, F\).
Ta có: \(OE // DC\) (gt)
\( \Rightarrow \dfrac{{OE}}{{DC}} = \dfrac{{AO}}{{AC}}\left( 1 \right)\) (hệ quả của định lí TaLet)
\(OF // DC\) (gt)
\( \Rightarrow \dfrac{{OF}}{{DC}} = \dfrac{{BO}}{{BD}}\left( 2 \right)\) (hệ quả của định lí TaLet)
\(AB // DC\) (gt)
\( \Rightarrow \dfrac{{OA}}{{OC}} = \dfrac{{OB}}{{OD}}\) (hệ quả của định lí TaLet)
\(\eqalign{
& \Rightarrow {{OC} \over {OA}} = {{OB} \over {OD}} \cr
& \Rightarrow {{OC} \over {OA}} + 1 = {{OD} \over {OB}} + 1 \cr
& \Rightarrow {{OC + OA} \over {OA}} = {{OD + OB} \over {OB}} \cr
& \Rightarrow {{AC} \over {OA}} = {{BD} \over {OB}} \cr
& \Rightarrow {{OA} \over {AC}} = {{OB} \over {BD}}\,\,\,\,(3) \cr} \)
Từ (1), (2) và (3) ta có:
\(\dfrac{{OE}}{{DC}} = \dfrac{{OF}}{{DC}} \Rightarrow OE = OF\)
Ta có: \(AB//EF\) (gt) áp dụng hệ quả của định lí TaLet ta có:
\(\begin{array}{l}
\Rightarrow \dfrac{{AN}}{{EO}} = \dfrac{{KN}}{{K{\rm{O}}}};\,\dfrac{{BN}}{{F{\rm{O}}}} = \dfrac{{KN}}{{K{\rm{O}}}}\\
\Rightarrow \dfrac{{AN}}{{EO}} = \dfrac{{BN}}{{F{\rm{O}}}} \\\text{Mà } EO=FO\\ \Rightarrow AN = BN
\end{array}\)
\( \Rightarrow \) \(N\) là trung điểm của \(AB.\)
Tương tự ta có: \(EF // DC\) (gt) áp dụng hệ quả của định lí TaLet ta có:
\(\begin{array}{l}
\Rightarrow \dfrac{{EO}}{{DM}} = \dfrac{{KO}}{{K{\rm{M}}}};\,\dfrac{{FO}}{{C{\rm{M}}}} = \dfrac{{KO}}{{K{\rm{M}}}}\\
\Rightarrow \dfrac{{EO}}{{DM}} = \dfrac{{FO}}{{C{\rm{M}}}}\\\text{Mà }EO=FO\\ \Rightarrow DM = CM
\end{array}\)
\( \Rightarrow M\) là trung điểm của \(CD\).
Vậy \(OK\) đi qua trung điểm của các cạnh \(AB\) và \(CD\).
5. Giải bài 60 trang 92 sgk Toán 8 tập 2
Cho tam giác vuông \(ABC\), và đường phân giác \(BD\) (\(D\) thuộc cạnh \(AC\)).
a) Tính tỉ số \(\dfrac{{A{\rm{D}}}}{{C{\rm{D}}}}\) .
b) Cho biết độ dài \(AB = 12,5 cm\). Hãy tính chu vi và diện tích của tam giác \(ABC\).
Bài giải:

a) Xét tam giác \(BCA\) vuông tại \(A\) (gt) có:
\(\begin{array}{l}
\widehat {ACB} + \widehat {ABC} = {90^0}\\
\Rightarrow \widehat {ABC} = {90^0} – \widehat {ACB} \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;= {90^0} – {30^0} = {60^0}
\end{array}\)
Trên tia đối của tia \(AB\) lấy điểm \(B’\) sao cho \(AB = AB’\) (1)
Xét hai tam giác vuông \(ABC\) và \(AB’C\) có:
\(AC\) chung (gt)
\(AB = AB’\) (gt)
\( \Rightarrow \Delta ABC = \Delta AB’C\) (cạnh góc vuông – cạnh góc vuông)
\( \Rightarrow BC = B’C\) (2 cạnh tương ứng)
\( \Rightarrow \Delta BB’C\) cân tại \(C\).
Lại có \(\widehat {ABC} = {60^0}\) nên suy ra \(\Delta BB’C\) đều (dấu hiệu nhận biết tam giác đều) (2)
Từ (1) và (2) \( \Rightarrow \dfrac{{AB}}{{BC}} = \dfrac{1}{2}\)
Vì \(BD\) là đường phân giác của \(\Delta ABC\) nên:
\(\dfrac{{DA}}{{DC}} = \dfrac{{BA}}{{BC}} = \dfrac{1}{2}\)
b) \(∆ABC\) vuông tại \(A\) nên áp dụng định lí Pitago ta có:
\(\eqalign{
& A{C^2} = B{C^2} – A{B^2},\,BC = 2AB \cr
& \Rightarrow A{C^2} = 4A{B^2} – A{B^2} = 3A{B^2} \cr
& \Rightarrow AC = \sqrt {3A{B^2}} = AB\sqrt 3 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 12,5\sqrt 3 \approx 21,65\,cm \cr} \)
Gọi \(p\) là chu vi \(∆ABC\)
\( \Rightarrow p = AB + BC + CA\)
\( \Rightarrow p = 3AB + AC = 3.12,5 + 12,5\sqrt 3 \)
\( \Rightarrow p = 12,5 (3+\sqrt 3 ) \approx 59,15\left( {cm} \right)\)
\({S_{ABC}} = \dfrac{1 }{ 2}AB.AC \approx 135,31(c{m^2})\)
6. Giải bài 61 trang 92 sgk Toán 8 tập 2
Tứ giác \(ABCD\) có \(AB = 4cm, BC = 20 cm\), \(CD = 25 cm, DA = 8cm\), đường chéo \(BD = 10cm\).
a) Nêu cách vẽ tứ giác \(ABCD\) có kích thước đã cho ở trên.
b) Các tam giác \(ABD\) và \(BDC\) có đồng dạng với nhau không? Vì sao?
c) Chứng minh rằng \(AB // CD\).
Bài giải:

a) Cách vẽ:
– Vẽ \(ΔBDC\):
+ Vẽ \(DC = 25cm\)
+ Vẽ cung tròn tâm \(D\) có bán kính \(10cm\) và cung tròn tâm \(C\) có bán kính \(20cm\). Giao điểm của hai cung tròn là \( B\).
– Vẽ điểm A: Vẽ cung tròn tâm \(B\) có bán kính \( 4cm\) và cung tròn tâm \(D\) có bán kính \( 8cm\). Giao điểm của hai cung tròn này là điểm \(A\).
Vậy là ta đã vẽ được tứ giác \(ABCD\) thỏa mãn điều kiện đề bài.
b) Ta có: \(\dfrac{{AB}}{{BD}} = \dfrac{4}{{10}} = \dfrac{2}{5};\) \(\dfrac{{BD}}{{DC}} = \dfrac{{10}}{{25}} = \dfrac{2}{5};\) \(\dfrac{{AD}}{{BC}} = \dfrac{8}{{20}} = \dfrac{2}{5}\)
\( \Rightarrow \dfrac{{AB}}{{BD}} = \dfrac{{BD}}{{DC}} = \dfrac{{AD}}{{BC}}\)
\(\Rightarrow \Delta AB{\rm{D}} \backsim \Delta B{\rm{D}}C\left( {c – c – c} \right)\)
c) \(∆ABD∽ ∆BDC\) (chứng minh trên)
\(\Rightarrow \widehat {ABD} = \widehat {BDC}\), mà hai góc ở vị trí so le trong.
\(\Rightarrow AB // DC\) hay \(ABCD\) là hình thang.
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 8 khác
- Để học tốt môn Vật lí lớp 8
- Để học tốt môn Sinh học lớp 8
- Để học tốt môn Ngữ văn lớp 8
- Để học tốt môn Lịch sử lớp 8
- Để học tốt môn Địa lí lớp 8
- Để học tốt môn Tiếng Anh lớp 8
- Để học tốt môn Tiếng Anh lớp 8 thí điểm
- Để học tốt môn Tin học lớp 8
- Để học tốt môn GDCD lớp 8
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 8 với giải bài 56 57 58 59 60 61 trang 92 sgk toán 8 tập 2!
“Bài tập nào khó đã có giaibaisgk.com“
