Hướng dẫn Giải bài 1 2 3 4 5 6 7 8 9 10 trang 39 40 sgk Hình học 12

Nội Dung

Hướng dẫn giải Bài §1. Khái niệm về mặt tròn xoay, Chương II. Mặt nón, mặt trụ, mặt cầu, sách giáo khoa Hình học 12. Nội dung bài giải bài 1 2 3 4 5 6 7 8 9 10 trang 39 40 sgk Hình học 12 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập hình học có trong SGK để giúp các em học sinh học tốt môn toán lớp 12.

Lý thuyết

1. Mặt nón – Hình nón – Khối nón

a) Mặt nón

Trong không gian cho hai đường thẳng $\Delta$ và $l$ cắt nhau tại O sao cho $(\widehat{\Delta ,l})=\alpha \, (0^{\circ}< \alpha < 90^{\circ}).$
Cho $l$ quay quanh $\Delta$ ta được mặt nón tròn xoay có:

$d$ là đường sinh.

$\Delta$ trục của mặt nón.

$O=l\cap \Delta$ đỉnh của mặt nón.

$2\alpha :$ góc ở đỉnh.

b) Hình nón

Cắt mặt nón tròn xoay đỉnh O, trục $\Delta$ bởi mặt phẳng (P) sao cho $(P)\perp \Delta ,O\notin (P).$

Hình giới hạn bởi mặt nón, mặt phẳng (P) được gọi là hình nón.

c) Khối nón

Khối nón tròn xoay là phần không gian giới hạn bởi hình nón tròn xoay kể cả hình nón đó.

d) Công thức tính diện tích và thể tích liên quan đến hình nón, khối nón

Cho hình nón có đường sinh $l$, bán kính đáy $R$, chiều cao $h$, ta có các công thức sau:

Thể tích khối nón: $V_{Khối \, \, nón}=\frac{1}{3}.S.h=\frac{1}{3}.\pi .R^{2}.h$.

Diện tích xung quanh hình nón: $S_{xq}=\pi Rl$.

Diện tích toàn phần hình nón: $S_{tp}=\pi Rl+\pi R^{2}$.

2. Mặt trụ – Hình trụ – Khối trụ

a) Mặt trụ

Trong không gian, cho đường thẳng $l$ song song và cách đường thẳng $\Delta$ một khoảng R.

Cho $l$ quay quanh $\Delta$ ta được một mặt tròn xoay được gọi là mặt trụ tròn xoay có:

$l$ là đường sinh.

$\Delta$ là trục mặt trụ.

$R$ là bán kính mặt trụ.

b) Hình trụ

Xét hình chữ nhật OABO’.

Cho đường gấp khúc OABO’ quay quanh OO’ ta được hình trụ tròn xoay:

OA: Bán kính đường tròn đáy.

AB: đường sinh.

c) Khối trụ

Khối trụ tròn xoay là phần không gian giới hạn bởi hình trụ tròn xoay kể cả hình trụ đó.

d) Các công thức tính toán liên quan đển hình trụ, khối trụ

Thể tích khối trụ: $V=\pi .R^2.h$ $=S_đáy.h$.

Diện tích xung quanh hình trụ: $S_{xq}=2\pi .R.h$.

Diện tích toàn phân hình trụ: $S_{tp}=2\pi .R.h+2\pi R^2$.

Trong đó: R: bán kính đáy; h: chiều cao (khoảng cách giữa hai đáy = OO’).

Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong phần hoạt động của học sinh trên lớp sgk Hình học 12.

Câu hỏi

1. Trả lời câu hỏi 1 trang 31 sgk Hình học 12

Hãy nêu tên một số đồ vật có hình dạng là các mặt tròn xoay.

Trả lời:

Một số đồ vật có hình dạng là các mặt tròn xoay: cái nón, lọ hoa, cái ốc, cuộn dây điện

2. Trả lời câu hỏi 2 trang 35 sgk Hình học 12

Cắt mặt xung quanh của một hình nón tròn xoay dọc theo một đường sinh rồi trải ra trên mặt phẳng ta được một nửa hình tròn bán kính $R$. Hỏi hình nón đó có bán kính r của đường tròn đáy và góc ở đỉnh của hình nón bằng bao nhiêu?

Trả lời:

Cắt mặt xung quanh của một hình nón tròn xoay dọc theo một đường sinh rồi trải ra trên mặt phẳng ta được một nửa hình tròn bán kính $R$ ⇒ đường sinh có độ dài bằng $R$ và chu vi đường tròn đáy bằng nửa chu vi đường tròn bán kính $R$.

$ \Rightarrow r = {R \over 2}$

Ta có: $\sin \widehat {{A_1}} = {r \over 1} = {r \over R} = {1 \over 2} \Rightarrow \widehat {{A_1}} = {30^0}$

Suy ra, góc ở đỉnh hình chóp: $\widehat A = 2\widehat {{A_1}} = {2.30^0} = {60^0}$

3. Trả lời câu hỏi 3 trang 38 sgk Hình học 12

Cho hình lập phương $ABCD.A’B’C’D’$ cạnh $a$. Tính diện tích xung quanh của hình trụ và thể tích của khối trụ có hai đáy là hai hình tròn ngoại tiếp hai hình vuông $ABCD và A’B’C’D’$.

Trả lời:

Biểu diễn đường tròn ngoại tiếp hình vuông $ABCD$ cạnh $a$ như hình vẽ

Khi đó: Tâm đường tròn là giao điểm $2$ đường chéo.

Bán kính đường tròn:

$r = IA = {{a\sqrt 2 } \over 2}$

Diện tích đường tròn là: $\pi {r^2} = {{{\pi a^2}} \over 2}$

⇒ diện tích xung quanh của hình trụ thỏa mãn đề bài (l = a) là:

${S_{xq}} = 2\pi rl = 2\pi a{{\sqrt 2 } \over 2}a = \pi {a^2}{{\sqrt 2 }}$

Diện tích khối trụ thỏa mãn đề bài (h = a) là:

$V = B.h = {{{\pi a^2}} \over 2}a = {{{\pi a^3}} \over 2}$

Dưới đây là Hướng dẫn giải bài 1 2 3 4 5 6 7 8 9 10 trang 39 40 sgk Hình học 12. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập hình học 12 kèm bài giải chi tiết bài 1 2 3 4 5 6 7 8 9 10 trang 39 40 sgk Hình học 12 của Bài §1. Khái niệm về mặt tròn xoay trong Chương II. Mặt nón, mặt trụ, mặt cầu cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 6 7 8 9 10 trang 39 40 sgk Hình học 12

1. Giải bài 1 trang 39 sgk Hình học 12

Cho đường tròn tâm $O$ bán kính $r$ nằm trên mặt phẳng $(P)$. Từ những điểm $M$ thuộc đường tròn này ta kẻ những đường thẳng vuông góc với $(P)$. Chứng minh rằng những đường thẳng như vậy nằm trên một mặt trụ tròn xoay. Hãy xác định trục và bán kính của mặt trụ đó.

Bài giải:

Gọi $d$ là đường thẳng vuông góc với mặt phẳng $(P)$ tại tâm $O$ của đường tròn $(T)$.

Từ điểm $M$ trên đường tròn $(T)$, vẽ đường thẳng $∆$ vuông góc với mặt phẳng $(P)$.

Khi đó đường thẳng $∆ // d$ và luôn cách $d$ một khoảng bằng $r.$

Đường thẳng $∆$ thuộc mặt trụ tròn xoay có trục là đường thẳng $d$ và bán kính $r$.

2. Giải bài 2 trang 39 sgk Hình học 12

Trong mỗi trường hợp sau đây, hãy gọi tên các hình tròn xoay hoặc khối tròn xoay sinh ra bởi:

a) Ba cạnh của hình chữ nhật khi quay quanh đường thẳng chứa cạnh thứ tư.

b) Ba cạnh của một tam giác cân khi quay quanh trục đối xứng của nó.

c) Một tam giác vuông kể cả các điểm trong của tam giác vuông đó khi quay quanh đường thẳng chứa một cạnh góc vuông.

d) Một hình chữ nhật kể cả các điểm trong của hình chữ nhật đó khi quay quanh đường thẳng chứa một cạnh.

Bài giải:

Theo định nghĩa ta thấy kết quả:

a) Khi xoay ba cạnh của hình chữ nhật khi quay quanh đường thẳng chứa cạnh thứ tư ta được hình trụ tròn xoay có đường cao là cạnh thứ tư còn bán kính hình trụ bằng độ dài của cạnh kề với cạnh thứ tư đó.

Ví dụ: Khi xoay ba cạnh của hình chữ nhật $ABCD$ quanh cạnh $CD$ ta đươc hình trụ tròn xoay có đường cao $CD$ và bán kính đáy $AD.$

b) Khi xoay ba cạnh của một tam giác cân khi quay quanh trục đối xứng nó ta được hình nón tròn xoay có chiều cao bằng chiều cao của tam giác cân, còn bán kính đáy bằng một nửa độ dài cạnh đáy của tam giác cân đó.

Ví dụ: Tam giác $ABC$ cân tại $A$ có trục đối xứng $AH$. Khi quay tam giác $ABC$ quanh $AH$ ta được hình nón có đường cao $Ah$ và bán kính đáy bằng $\frac{BC}{2}$.

c) Khi xoay một tam giác vuông kể cả các điểm trong của tam giác vuông đó khi quay quanh đường thẳng chứa một cạnh góc vuông ta được khối nón tròn xoay.

d) Khi xoay một hình chữ nhật kể cả các điểm trong của hình chữ nhật đó khi quay quanh đường thẳng chứa một cạnh ta được khối trụ tròn xoay.

3. Giải bài 3 trang 39 sgk Hình học 12

Một hình nón có đường cao $h = 20cm$, bán kính đáy $r = 25cm$.

a) Tính diện tích xung quanh của hình nón đã cho.

b) Tính thể tích của khối nón được tạo thành bởi hình nón đó.

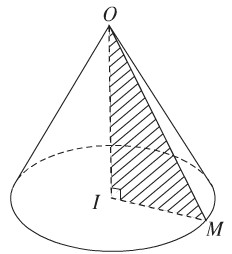
c) Một thiết diện đi qua đỉnh của hình nón và khoảng cách từ tâm của đáy đến mặt phẳng thiết diện là 12cm. Tính diện tích thiết diện đó.

Bài giải:

a) Giả sử $SA = l$ là độ dài đường sinh, $SH = h$ là chiều cao hình nón.

Trong tam giác vuông $SOA$ ta có:

$SA^{2}=SO^{2}+OA^{2}=h^{2}+r^{2}=20^{2}+25^{2}=1025$

⇒ $SA=\sqrt{1025}$

Diện tích xung quanh hình nón là:

$S_{xq}=π.r.l=π.25\sqrt{1025}≈2514,5(cm^{2})$

b) Thể tích khối nón là:

$V=\frac{1}{3}π.r^{2}.h=\frac{1}{3}π.25^{2}.20≈13083,3(cm^{3})$

c) Giả sử thiết diện SAB đi qua đỉnh S cắt đường tròn đáy tại A và B. Gọi I là trung điểm cỉa dây cung AB. Từ tâm O của đáy vẽ OH vuông góc với SI.

Ta có: $\left\{\begin{matrix}AB\perp OI & \\ AB\perp SO & \end{matrix}\right.⇒ AB\perp (SOI)$

⇒ $AB\perp OH$

Mà: $\left\{\begin{matrix}OH\perp AH & \\ OH\perp SI & \end{matrix}\right.⇒ OH\perp (SAB)$

⇒ $OH=12(cm)$

Xét tam giác vuông SOI, có: $\frac{1}{OH^{2}}=\frac{1}{OI^{2}}+\frac{1}{OS^{2}}$

⇒ $\frac{1}{OI^{2}}=\frac{1}{OH^{2}}-\frac{1}{OS^{2}}$

⇒ $\frac{1}{OI^{2}}=\frac{1}{12^{2}}-\frac{1}{20^{2}}$

⇒ $OI=15(cm)$

Xét tam giác vuông AOI, có: $AI^{2}=OA^{2}-OI^{2}=25^{2}-15^{2}=20^{2}$

⇒ $AI=20(cm)$

Mặt khác: $SI.OH=SO.OI ⇒ SI=\frac{SO.OI}{OH}$

⇒ $SI=\frac{20.15}{12}=15(cm)$

⇒ Diện tích thiết diện $SAB$ là:

$S_{SAB}=\frac{1}{2}SI.AB=25.20=500(cm^{2})$

4. Giải bài 4 trang 39 sgk Hình học 12

Trong không gian cho hai điểm $A, B$ cố định và có độ dài $AB = 20 cm$,. Gọi $d$ là một đường thẳng thay đổi luôn luôn đi qua $A$ và cách $B$ một khoảng bằng $10 cm$. Chứng tỏ rằng đường thẳng $d$ luôn luôn nằm trên một mặt nón, hãy xác định trục và góc ở đỉnh của mặt nón đó.

Bài giải:

Kẻ $BH\perp d ⇒ BH = 10cm$

Ta có: $\sin \alpha =\frac{BH}{AB}=\frac{1}{2}$

⇒ $\alpha =30^{\circ}$

Vậy đường thẳng d luôn thuộc mặt nón nhận đường thẳng $AB$ làm trục và có góc ở đỉnh bằng:

$2\alpha =2.30^{\circ}=60^{\circ}$

5. Giải bài 5 trang 39 sgk Hình học 12

Một hình trụ có bán kính đáy $r = 5cm$ và có khoảng cách giữa hai đáy bằng $7 cm$.

a) Tính diện tích xung quanh của hình trụ và thể tích của khối trụ được tạo nên.

b) Cắt khối trụ bởi một mặt phẳng song song với trục và cách trục $3 cm$. Hãy tính diện tích của thiết diện được tạo nên.

Bài giải:

a) Theo đầu bài, hình trụ có chiều cao $h = 7 cm$ và bán kính đáy $r = 5 cm$.

Vậy diện tích xung quanh bằng: $S_{xq}= 2πrh = 140π$($cm^2$)

Thể tích của khối trụ là: $V = πr^2h = 175π$ ($cm^3$)

b) Thiết diện là hình chữ nhật có một cạnh bằng chiều cao của hình trụ bằng $7 cm$. Giả sử thiết diện là $ABB_1A_1$. Ta có $AA_1 = 7 cm$.

Gọi H là trung điểm của AB ta có: $d\left( {O;\left( {AB{B_1}{A_1}} \right)} \right) = OH = 3cm$.

Do tam giác $OAH$ vuông tại $H$ (quan hệ vuông góc giữa đường kính và dây cung) nên áp dụng định lí Pitago ta có: $AH^2 = OA^2 – OH^2 = 25 – 9 = 16$.

$\Rightarrow AH = 4 cm \Leftrightarrow AB = 8 cm$.

Vậy diện tích của thiết diện là: $S=AB.AA_1=8.7=56$ ($cm^2$).

6. Giải bài 6 trang 39 sgk Hình học 12

Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều cạnh $2a$.

Tính diện tích xung quanh và thể tích của hình nón đó.

Bài giải:

Theo đề bài, đường kính của hình tròn đáy của nón bằng $2a$. Vậy bán kính $R = a$ và độ dài đường sinh cua hình nón $l = 2a$.

Suy ra chiều cao của hình nón là:

$h = \sqrt {{l^2} – {r^2}} = \sqrt {4{a^2} – {a^2}} = a\sqrt 3 $

Vậy diện tích xung quanh của hình nón là:

$S_{xq} = πRl = π.a.2a=2a^2π$

Thể tích khối nón là:

$V = {1 \over 3}\pi {r^2}.h = {1 \over 3}\pi {a^2}.a\sqrt 3 = {{\pi {a^3}\sqrt 3 } \over 3}$

7. Giải bài 7 trang 39 sgk Hình học 12

Một hình trụ có bán kính $r$ và chiều cao $h = r\sqrt3$.

a) Tính diện tích xung quanh và diện tích toàn phần của hình trụ.

b) Tính thể tích khối trụ tạo nên bởi hình trụ đã cho.

c) Cho hai điểm $A$ và $B$ lần lượt nằm trên hai đường tròn đáy sao cho góc giữa đường thẳng $AB$ và trục của hình trụ bằng $30^0$. Tính khoảng cách giữa đường thẳng $AB$ và trục của hình trụ.

Bài giải:

Để giải quyết tốt bài toán này, các bạn chỉ cần nhớ công thức tính diện tích xung quanh và thể tích khối trụ.

a) Diện tích xung quanh của hình trụ là:

$S_{xq} = 2π.r.h = 2\sqrt{3}.π.r^{2}$ (đvdt)

Diện tích toàn phần của hình trụ là:

$S_{tp} = 2π.r.h + 2π.r^{2} = 2\sqrt{3}π.r^{2} + 2π.r^{2} = 2(\sqrt{3} + 1)π.r^{2}$ (đvtt)

b) Thể tích khối trụ tạo nên bởi hình trụ đã cho là:

$V_{trụ} = π.R^{2}.h = \sqrt{3}π. r^{3}$ (đvtt)

c) Giả sử trục của hình trụ là $O_1O_2$ và $A$ nằm trên đường tròn tâm $O_1$, $B$ nằm trên đường tròn tâm $O_2$; $I$ là trung điểm của $O_1O_2$ , $J$ là trung điểm của $AB$.

Ta chứng minh $IJ$ là đường vuông góc chung của $O_1O_2$ và $AB$.

Hạ $BB_1$ vuông góc với đáy, $J_1$ là hình chiếu vuông góc của $J$ xuống đáy.

Dễ thấy $J_1$ là trung điểm của $AB_1$ (định lí đường trung bình của tam giác).

Ta có: $\left\{ \begin{array}{l}{O_1}{J_1} \bot A{B_1}\\{O_1}{J_1} \bot B{B_1}\end{array} \right. \Rightarrow {O_1}{J_1} \bot \left( {AB{B_1}} \right)$.

Mà $IJ//{O_1}{J_1} \Rightarrow IJ \bot \left( {AB{B_1}} \right)$ $ \Rightarrow IJ \bot AB$.

$\left\{ \begin{array}{l}IJ//{O_1}{J_1}\\{O_1}{O_2} \bot {O_1}{J_1}\end{array} \right. \Rightarrow IJ \bot {O_1}{O_2}$.

Vậy IJ là đường vuông góc chung của $O_1O_2$ và $AB$ $ \Rightarrow d\left( {AB;{O_1}{O_2}} \right) = IJ$

Ta có: $BB_1$ // ${O_1}{O_2}$ $ \Rightarrow \widehat {\left( {AB;{O_1}{O_2}} \right)} = \widehat {\left( {AB;B{B_1}} \right)} = \widehat {AB{B_1}}$.

do vậy: $AB_1 = BB_1.tan 30^0$ = $ \frac{\sqrt{3}}{3}h = r$.

Xét tam giác vuông $O_1J_1A$ vuông tại $J_1$ ta có:

$ O_{1}J^{2}_{1}$ = $ O_{1}A^{2}$ – $ AJ^{2}_{1} =$ $ r^{2} – {\left( {{r \over 2}} \right)^2}=$ $ \frac{3}{4}r^{2}$ $ \Rightarrow {O_1}{J_1} = \frac{{r\sqrt 3 }}{2}$

Vậy khoảng cách giữa $AB$ và $O_1O_2$ là: $ \frac{\sqrt{3}}{2}r$.

8. Giải bài 8 trang 40 sgk Hình học 12

Một hình trụ có hai đáy là hai hình tròn $(O;r)$ và $(O’;r)$. Khoảng cách giữa hai đáy là $OO’ = r.\sqrt3$. Một hình nón có đỉnh là $O’$ và có đáy là hình tròn $(O;r)$.

a) Gọi $S_1$ là diện tích xung quanh của hình trụ và $S_2$ là diện tích xung quanh của hình nón, hãy tính tỷ số ${{{S_1}} \over {{S_2}}}$.

b) Mặt xung quanh của hình nón chia khối trụ thành hai phần, hãy tính tỷ số thể tích hai phần đó.

Bài giải:

a) Hình trụ có chiều cao $l = h = r\sqrt3$ và bán kính đáy $r$ nên diện tích xung quanh hình trụ là:

\[S_1 = 2πr.h = 2πr.r\sqrt3 = 2\sqrt3 πr^2\]

Với $M$ là một điểm bất kì thuộc đường tròn $(O)$ thì $O’M$ là một đường sinh của hình nón ta có:

$l’ = O’M = \sqrt {OO{‘^2} + O{M^2}} = \sqrt {3{r^2} + {r^2}} = 2r$

Hình nón có bán kính đáy $r$ và độ dài đường sinh $l=2r$ nên diện tích xung quanh hình nón là:

\[S_2 = πrl’= π.r.2r = 2πr^2\]

Vậy: ${{{S_1}} \over {{S_2}}} = {{2\sqrt 3 \pi {r^2}} \over {2\pi {r^2}}} = \sqrt 3 $

b) Mặt xung quanh của hình nón chia khối trụ thành hai phần: Phần dưới là khối nón và phần còn lại.

Gọi V là thể tích khối trụ ta có:

$V = \pi {r^2}h$

Gọi $V_1$ là thể tích khối nón ta có:

${V_1} = \frac{1}{3}\pi {r^2}h$

Gọi $V_2$ là thế tích phần còn lại ta có:

${V_2} = V – {V_1} = \pi {r^2}h – \frac{1}{3}\pi {r^2}h = \frac{2}{3}\pi {r^2}h$

Vậy tỉ số $\frac{{{V_1}}}{{{V_2}}} = \frac{{\frac{1}{3}\pi {r^2}h}}{{\frac{2}{3}\pi {r^2}h}} = \frac{1}{2}$.

9. Giải bài 9 trang 40 sgk Hình học 12

Cắt hình nón đỉnh $S$ bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng $a\sqrt2$.

a) Tính diện tích xuang quanh, diện tích đáy và thể tích của khối nón tương ứng.

b) Cho một dây cung $BC$ của đường tròn đáy hình nón sao cho mặt phẳng $(SBC)$ tạo với mặt phẳng chứa đáy hình nón một góc $60^0$. Tính diện tích tam giác $SBC$.

Bài giải:

a) Tam giác $SAB$ vuông cân tại S nên $SA = SB = a$.

Cạnh huyền chính bằng đường kính đáy do vậy bán kính đáy $r = \frac{a\sqrt{2}}{2}$, đường sinh $l = a$.

Gọi $h$ là độ dài đường cao của hình nón ta có: $h = \sqrt {{l^2} – {r^2}} = \sqrt {{a^2} – \frac{{{a^2}}}{2}} = \frac{{a\sqrt 2 }}{2}$.

Vậy $S_{xq} = πrl =$ $ \frac{\sqrt{2}}{2}\pi a^2$ ( đơn vị diện tích)

$S_{đáy}$ = $ \pi r^{2}$ = $ \pi \frac{a^{2}}{2}$ ( đơn vị diện tích);

$V$nón = $ \frac{1}{3}\pi r^{2}h$ $ = \frac{\sqrt{2}}{12}\pi a^{3}$ ( đơn vị thể tích)

b) Gọi tâm đáy là $O$ và trung điểm cạnh $BC$ là $M$ ta có: ${OM \bot BC}$ (quan hệ vuông góc giữa đường kính và dây cung).

Ta có:

\[\begin{array}{l}
\left\{ \begin{array}{l}
BC \bot OM\\
BC \bot SO
\end{array} \right. \Rightarrow BC \bot \left( {SOM} \right) \Rightarrow BC \bot SM\\
\left\{ \begin{array}{l}
\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\
SM \bot BC\\
OM \bot BC
\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SM;OM} \right)} = \widehat {SMO} = {60^0}
\end{array}\]

Ta có: $SM = \frac{{SO}}{{\sin 60}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{\frac{{\sqrt 3 }}{2}}} = \frac{{a\sqrt 6 }}{3}$.

$OM = SO.\cot 60 = \frac{{a\sqrt 2 }}{2}.\frac{1}{{\sqrt 3 }} = \frac{{a\sqrt 6 }}{6}$

Ta có $∆ OMB$ vuông ở $M$ nên $ BM^{2}= BO^{2} – OM^{2} = \frac{a^{2}}{3}$

Vậy $BM = \frac{a}{\sqrt{3}}\Rightarrow BC =2BM= \frac{2a}{\sqrt{3}}$.

Do đó $S = {{SM.BC}\over2}$ = $ \frac{\sqrt{2}}{3}a^{2}$ (đơn vị diện tích)

10. Giải bài 10 trang 40 sgk Hình học 12

Cho hình trụ có bán kính $r$ và có chiều cao cũng bằng $r$. Một hình vuông $ABCD$ có hai cạnh $AB$ và $CD$ lần lượt là các dây cung của hai đường tròn đáy, còn cạnh $BC$ và $AD$ không phải là đường sinh của hình trụ. Tính diện tích của hình vuông đó và cosin của góc giữa mặt phẳng chứa hình vuông và mặt phẳng đáy.

Bài giải:

Do tính chất đối xứng của $(ABCD)$ nên $(ABCD)$ cắt $OO’$ tại trung điểm $I$ của $OO’$. $I$ cũng là giao điểm của hai đường chéo $AC,BD$.

Xét tam giác vuông $IOB$ ta có: $IB^2=IO^2+OB^2$

$\Rightarrow IB=\sqrt {{{\left( {{r \over 2}} \right)}^2} + {r^2}} = {{r\sqrt 5 } \over 2}$

$\Rightarrow AC=BD=2IB=r\sqrt5$.

Do ABCD là hinh vuông nên $AB= \frac{{AC}}{{\sqrt 2 }}={{r\sqrt {10} } \over 2}$

Vậy $S_{ABCD}={AB}^2={{5{r^2}} \over 2}$.

Gọi $E$ là trung điểm của $AB$

$\Rightarrow OE\bot AB, IE\bot AB$.

$\Rightarrow \widehat {IEO}$ là góc giữa $(ABCD)$ và mặt đáy của hình trụ.

Ta có: $IE = \frac{1}{2}AD ={{r\sqrt {10} } \over 4}, OI={r\over 2}$.

Xét tam giác vuông IOE có: $OE = \sqrt {I{E^2} – O{I^2}} = \sqrt {{{\left( {\frac{{r\sqrt {10} }}{4}} \right)}^2} – {{\left( {\frac{r}{2}} \right)}^2}} = \frac{{r\sqrt 6 }}{4}$.

$cos\widehat {IEO}={{OE}\over {IE}}={\sqrt{15}\over5}$

Bài trước:

Ôn tập chương I: Giải bài tập trắc nghiệm 1 2 3 4 5 6 7 8 9 10 trang 27 28 sgk Hình học 12

Bài tiếp theo:

Giải bài 1 2 3 4 5 6 7 8 9 10 trang 48 49 sgk Hình học 12

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 12 với giải bài 1 2 3 4 5 6 7 8 9 10 trang 39 40 sgk Hình học 12!

“Bài tập nào khó đã có giaibaisgk.com“