Nội Dung
Hướng dẫn giải Bài §1. Giới hạn của dãy số, Chương IV. Giới hạn, sách giáo khoa Đại số và Giải tích 11. Nội dung bài giải bài 1 2 3 4 5 6 7 8 trang 121 122 sgk Đại số và Giải tích 11 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập đại số và giải tích có trong SGK để giúp các em học sinh học tốt môn toán lớp 11.
Lý thuyết
1. Giới hạn hữu hạn của dãy số
\( \bullet \) Dãy số \(({u_n})\) được gọi là có giới hạn bằng 0 khi n tiến ra dương vô cực nếu với mỗi số dương nhỏ tuỳ ý cho trước, mọi số hạng của dãy số , kể từ một số hạng nào đó trở đi, đều có giá tri tuyệt dối nhỏ hơn số dương đó. Kí hiệu: \(\mathop {\lim }\limits_{x \to + \infty } {u_n} = 0\) .Hay là: \(\mathop {\lim }\limits_{x \to 0} {u_n} = 0\) khi và chỉ khi với mọi \(\varepsilon > 0\) nhỏ tùy ý, luôn tồn tại số tự nhiên \({n_0}\) sao cho: \(\left| {{u_n}} \right| < \varepsilon ,{\rm{ }}\forall n > {n_0}\).
\( \bullet \)\(\mathop {\lim }\limits_{x \to + \infty } {u_n} = a \Leftrightarrow \mathop {\lim }\limits_{x \to + \infty } \left( {{u_n} – a} \right) = 0\), tức là: Với mọi \(\varepsilon > 0\) nhỏ tùy ý, luôn tồn tại số tự nhiên \({n_0}\) sao cho \(\left| {{u_n} – a} \right| < \varepsilon ,{\rm{ }}\forall n > {n_0}\).
Dãy số (un) có giới hạn là số thực gọi là dãy số có giới hạn hữu hạn.
Một số giới hạn đặc biệt:
\(\bullet \) \(\lim \frac{1}{{{n^k}}} = 0\) với \(k \in \mathbb{N}*\)
\(\bullet \) Nếu \(\left| q \right| < 1\) thì \(\mathop {\lim }\limits_{n \to + \infty } {q^n} = 0\)
\(\bullet \) Nếu \({u_n} = c\) (với \(c\) là hằng số) thì \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = \mathop {\lim }\limits_{n \to + \infty } c = c\)
Chú ý: Ta viết \(\lim {u_n} = a\) thay cho cách viết \(\mathop {\lim }\limits_{n \to + \infty } {u_n} = a\).
2. Một số định lí về giới hạn
Định lí 1: Nếu dãy số (un) thỏa \(\left| {{u_n}} \right| < {v_n}\) kể từ số hạng nào đó trở đi và \(\lim {v_n} = 0\) thì \(\lim {u_n} = 0\).
Định lí 2: Cho \(\lim {u_n} = a,{\rm{ }}\lim {v_n} = b\). Ta có:
\(\bullet \)\(\lim ({u_n} + {v_n}) = a + b\)
\(\bullet \)\(\lim ({u_n} – {v_n}) = a – b\)
\(\bullet \) \(\lim ({u_n}.{v_n}) = a.b\)
\(\bullet \) \(\lim \frac{{{u_n}}}{{{v_n}}} = \frac{a}{b}{\rm{ (}}b \ne 0)\)
\(\bullet \) Nếu \({u_n} \ge 0{\rm{ }}\forall n\) thì \(\lim \sqrt {{u_n}} = \sqrt a \)
3. Tổng của CSN lùi vô hạn
Cho CSN \(({u_n})\) có công bội q thỏa \(\left| q \right| < 1\). Khi đó tổng
\(S = {u_1} + {u_2} + … + {u_n} + ….\) gọi là tổng vô hạn của CSN và
\(S = \lim {S_n} = \lim \frac{{{u_1}(1 – {q^n})}}{{1 – q}} = \frac{{{u_1}}}{{1 – q}}\).
4. Giới hạn vô cực
\(\bullet \)\(\mathop {\lim }\limits_{n \to + \infty } {u_n} = + \infty \Leftrightarrow \) với mỗi số dương tuỳ ý cho trước , mọi số hạng của dãy số , kể từ một số hạng nào đó trở đi, đều lớn hơn số dương đó .
\(\bullet \)\(\mathop {\lim }\limits_{n \to + \infty } {u_n} = – \infty \Leftrightarrow \mathop {\lim }\limits_{n \to + \infty } \left( { – {u_n}} \right) = + \infty \).
Một số kết quả đặc biệt:
\(\bullet \)\(\lim {n^k} = + \infty \) với mọi \(k > 0\)
\(\bullet \) \(\lim {q^n} = + \infty \) với mọi \(q > 1\).
Một vài quy tắc tìm giới hạn vô cực:
Quy tắc 1: Nếu \(\lim {u_n} = \pm \infty \), \(\lim {v_n} = \pm \infty \) thì \(\lim ({u_n}.{v_n})\) được cho như sau:
| \(\lim {u_n}\) | \(\lim {v_n}\) | \(\lim ({u_n}{v_n})\) |
| \( + \infty \)
\( + \infty \) \( – \infty \) \( – \infty \) |
\( + \infty \)
\( – \infty \) \( + \infty \) \( – \infty \) |
\( + \infty \) \( – \infty \) \( – \infty \) \( + \infty \) |
Quy tắc 2: Nếu \(\lim {u_n} = \pm \infty \), \(\lim {v_n} = l\) thì \(\lim ({u_n}.{v_n})\) được cho như sau:
| \(\lim {u_n}\) | Dấu của \(l\) | \(\lim ({u_n}{v_n})\) |
| \( + \infty \)
\( + \infty \) \( – \infty \) \( – \infty \) |
\( + \)
\( – \) \( + \) \( – \) |
\( + \infty \) \( – \infty \) \( – \infty \) \( + \infty \) |
Quy tắc 3: Nếu \(\lim {u_n} = l\),\(\lim {v_n} = 0\) và \({v_n} > 0\) hoặc \({v_n} < 0\) kể từ một số hạng nào dó trở đi thì \(\lim \frac{{{u_n}}}{{{v_n}}}\) được coi như sau:
| Dấu của \(l\) | Dấu của \({v_n}\) | \(\lim \frac{{{u_n}}}{{{v_n}}}\) |
| \( + \infty \)
\( + \infty \) \( – \infty \) \( – \infty \) |
\( + \)
\( – \) \( + \) \( – \) |
\( + \infty \) \( – \infty \) \( – \infty \) \( + \infty \) |
Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong phần hoạt động của học sinh sgk Đại số và Giải tích 11.
Câu hỏi
1. Trả lời câu hỏi 1 trang 112 sgk Đại số và Giải tích 11
Cho dãy số (un) với un = $\dfrac{1}{n}$.
Biểu diễn \(({u_n})\) dưới dạng khai triển:
\(1,\,{1 \over 2};\,{1 \over 3};\,{1 \over 4};\,{1 \over 5};…..;{1 \over {100}}\)
Biểu diễn (un) trên trục số (h.46):

a) Nhận xét xem khoảng cách từ un tới 0 thay đổi như thế nào khi n trở nên rất lớn.
b) Bắt đầu từ số hạng un nào của dãy số thì khoảng cách từ un đến 0 nhỏ hơn $0,01? 0,001$?
Trả lời:
a) Khoảng cách từ \({u_n}\) tới 0 trở nên rất nhỏ (gần bằng 0) khi n trở nên rất lớn
b) Ta có: \(\dfrac{1}{n} < 0,01 \Leftrightarrow \dfrac{1}{n} < \dfrac{1}{{100}}\) \( \Leftrightarrow n > 100\).
Do đó từ số hạng thứ \(101\) thì khoảng cách từ \({u_n}\) đến \(0\) đều nhỏ hơn \(0,01\).
\(\dfrac{1}{n} < 0,001 \Leftrightarrow \dfrac{1}{n} < \dfrac{1}{{1000}}\) \( \Leftrightarrow n > 1000\).
Do đó từ số hạng thứ \(1001\) thì khoảng cách từ \({u_n}\) đến \(0\) đều nhỏ hơn \(0,001\).
2. Trả lời câu hỏi 2 trang 117 sgk Đại số và Giải tích 11
Có nhiều tờ giấy chồng nhau, mỗi tờ có bề dày là $0,1 mm$. Ta xếp chồng liên tiếp tờ này lên tờ khác (h.48). Giả sử có thể thực hiện việc xếp giấy như vậy một cách vô hạn.
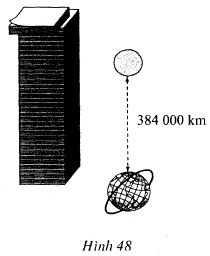
Gọi u1 là bề dày của một tờ giấy, u2 là bề dày của một xếp giấy gồm hai tờ, u3 là bề dày của một xếp giấy gồm ba tờ, …, un là bề dày của một xếp giấy gồm n tờ. Tiếp tục như vậy t được dãy số vô hạn (un).
Bảng sau đây cho biết bề dày (tính theo mm) của một số chồng giấy.

a) Quan sát bảng trên và nhận xét về giá trị của un khi $n$ tăng lên vô hạn.
b) Với $n$ như thế nào thì ta đạt được những chồng giấy có về dày lớn hơn khoảng cách từ Trái Đất tới Mặt Trăng? (Cho biết khoảng cách này ở một thời điểm xác định là $384000 km$ hay 384.109 mm)
Trả lời:
a) Giá trị của un rất lớn khi $n$ tăng lên vô hạn.
b) Ta có: \({u_n} > {384.10^9}\) \( \Leftrightarrow \dfrac{n}{{10}} > {384.10^9}\) \( \Leftrightarrow n > {384.10^{10}}\).
Vậy cần \(n > {384.10^{10}}\) tờ giấy để đạt được những chồng giấy có về dày lớn hơn khoảng cách từ Trái Đất tới Mặt Trăng.
Dưới đây là phần Hướng dẫn giải bài 1 2 3 4 5 6 7 8 trang 121 122 sgk Đại số và Giải tích 11. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập đại số và giải tích 11 kèm bài giải chi tiết bài 1 2 3 4 5 6 7 8 trang 121 122 sgk Đại số và Giải tích 11 của Bài §1. Giới hạn của dãy số trong Chương IV. Giới hạn cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 1 trang 121 sgk Đại số và Giải tích 11
Có \(1 kg\) chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian \(T = 24 000\) năm thì một nửa số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (\(T\) được gọi là chu kì bán rã).
Gọi \((u_n)\) là khối lượng chất phóng xạ còn sót lại sau chu kì thứ \(n\).
a) Tìm số hạng tổng quát \(u_n\) của dãy số \((u_n)\).
b) Chứng minh rằng \((u_n)\) có giới hạn là \(0\).
c) Từ kết quả câu b), chứng tỏ rằng sau một số năm nào đó khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với con người, cho biết chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn \(10^{-6}g\).
Bài giải:
a) Ta có: \(u_1=\frac{1}{2}\); \(u_2= \frac{1}{4}\); \(u_3=\frac{1}{8}\); … .
Từ đó ta dự đoán công thức \(u_n=\frac{1}{2^{n}}\) \(\forall n \ge 1\).
Điều này chứng minh đơn giản bằng quy nạp.
Hiển nhiên công thức trên đúng với \(n=1\).
Giả sử công thức đúng với mọi \(k \ge 1\), tức là có \(u_k=\frac {1} {2^k}\), ta chứng minh công thức đó đúng với mọi \(n=k+1\), tức là cần chứng minh: \(u_{k+1}=\frac {1} {2^{k+1}}\).
Ta có \({u_{k + 1}} = \frac{{{u_k}}}{2} = \frac{1}{{{2^k}}}:2 = \frac{1}{{{2^k}}}.\frac{1}{2} = \frac{1}{{{2^{k + 1}}}}\).
Vậy \({u_n} = \frac{1}{{{2^n}}}\,\,\forall n \in {N^*}\).
b) \(\lim {u_n} = \lim {\left( {{1 \over 2}} \right)^n} = 0\).
c) Đổi \(10^{-6}g = \frac{1}{10^{6}} . \frac{1}{10^{3}}kg = \frac{1}{10^{9}} kg\).
Muốn có \(u_n= \frac{1}{2^{n}}\) < \(\frac{1}{10^{9}}\), ta cần chọn \(n_0\) sao cho \({2^{{n_0}}} > {10^9}\). Suy ra \(n_0= 30\). Nói cách khác, sau chu kì thứ \(30\) (nghĩa là sau \(30.24000 = 720000\) (năm)), chúng ta không còn lo lắng về sự độc hại của khối lượng chất phóng xạ còn lại.
2. Giải bài 2 trang 121 sgk Đại số và Giải tích 11
Biết dãy số \((u_n)\) thỏa mãn \(|u_n-1| < \frac{1}{n^{3}}\) với mọi \(n\). Chứng minh rằng \(\lim u_n=1\).
Bài giải:
Vì \(\lim \frac{1}{n^{3}}\) = 0 nên |\(\frac{1}{n^{3}}\)| có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi.
Mặt khác, ta có \(|u_n-1| < \frac{1}{n^{3}}\) = |\(\frac{1}{n^{3}}\)| với mọi \(n\). Nếu \(|u_n-1|\) có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở đi, nghĩa là \(\lim (u_n-1) = 0\). Do đó \(\lim u_n= 1\).
Hoặc:
Ta có:
\(\left\{ \begin{array}{l}
\lim \frac{1}{{{n^3}}} = 0 \Rightarrow \lim \left| {{u_n} – 1} \right| \le 0\\
\left| {{u_n} – 1} \right| \ge 0 \Rightarrow \lim \left| {{u_n} – 1} \right| \ge 0
\end{array} \right. \) \(\Rightarrow \lim \left| {{u_n} – 1} \right| = 0 \Leftrightarrow \lim {u_n} = 1\)
3. Giải bài 3 trang 121 sgk Đại số và Giải tích 11
Tìm giới hạn sau:
a) \(\lim \frac{6n – 1}{3n +2}\);
b) \(\lim \frac{3n^{2}+n-5}{2n^{2}+1}\);
c) \(\lim \frac{3^{n}+5.4^{n}}{4^{n}+2^{n}}\);
d) \(\lim\frac{\sqrt{9n^{2}-n+1}}{4n -2}\).
Bài giải:
Ta có:
a) \(\lim \frac{6n – 1}{3n +2}\)
\(= \lim\frac{6 – \frac{1}{n}}{3 +\frac{2}{n}}\) = \(\frac{6}{3} = 2\).
b) \(\lim \frac{3n^{2}+n-5}{2n^{2}+1}\)
\( = \lim \frac{3 +\frac{1}{n}-\frac{5}{n^{2}}}{2+\frac{1}{n^{2}}}= \frac{3}{2}\).
c) \(\lim \frac{3^{n}+5.4^{n}}{4^{n}+2^{n}}\)
\(= \lim \frac{{\left( {{3 \over 4}} \right)^n}+5}{1+{\left( {{1 \over 2}} \right)^n}}=\frac{5}{1}\) = 5.
d) \(\lim \frac{\sqrt{9n^{2}-n+1}}{4n -2}\)
= \(\lim \frac{\sqrt{{n^2}\left( {9 – {1 \over n} + {1 \over {{n^2}}}} \right)}}{n(4-\frac{2}{n})}\)
= \(\lim \frac{\sqrt{9-\frac{1}{n}+\frac{1}{n^{2}}}}{4-\frac{2}{n}}\)
=\(\frac{\sqrt{9}}{4}\)= \(\frac{3}{4}\).
4. Giải bài 4 trang 122 sgk Đại số và Giải tích 11
Để trang hoàng cho căn hộ của mình, chú chuột Mickey quyết định tô màu một miếng bìa hình vuông cạnh bằng \(1\). Nó tô màu xám các hình vuông nhỏ được đánh dấu \(1, 2, 3, …, n, …\) trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó (h.51).
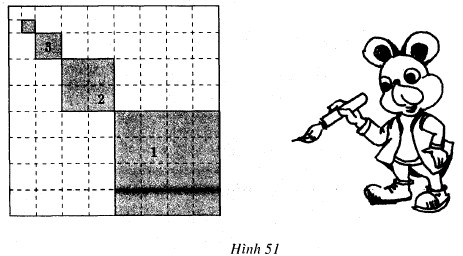
Giả sử quy trình tô màu của Mickey có thể tiến ra vô hạn.
a) Gọi \(u_n\) là diện tích của hình vuông màu xám thứ \(n\). Tính \(u_1, u_2, u_3\) và \(u_n\).
b) Tính \(\lim S_n\) với \(S_n= {u_{1}} + {u_{2}} + {u_{3}} + … + {u_{n}}\)
Bài giải:
a) Hình vuông thứ nhất có cạnh bằng \(\frac{1}{2}\) nên
\(u_1 =(\frac{1}{2}\))2 = \(\frac{1}{4}\).
Hình vuông thứ hai có cạnh bằng \(\frac{1}{4}\) nên \({u_2} = {\left( {{1 \over 4}} \right)^2} = {1 \over {{4^2}}}\).
Hình vuông thứ ba có cạnh bằng \(\frac{1}{8}\) nên \({u_3} = {\left( {{1 \over 8}} \right)^2} = {1 \over {{4^3}}}\)
Tương tự, ta có \(u_n=\frac{1}{4^{n}}\)
b) Dãy số \((u_n)\) là một cặp số nhân lùi vô hạn với \(u_1=\frac{1}{4}\) và \(q = \frac{1}{4}\). Do đó
\(\lim S_n=\frac{u_{1}}{1-q}= \frac{\frac{1}{4}}{1-\frac{1}{4}}=\frac{1}{3}\).
5. Giải bài 5 trang 122 sgk Đại số và Giải tích 11
Tính tổng \(S = -1 + \frac{1}{10}- \frac{1}{10^{2}} + … + \frac{(-1)^{n}}{10^{n-1}}+ …\)
Bài giải:
Các số hạng tổng lập thành cấp số nhân lùi vô hạn với \({u_1} = – 1\) và \(q = – {1 \over {10}}\)
Vậy \(S = -1 +\frac{1}{10} – \frac{1}{10^{2}}+ … + \frac{(-1)^{n}}{10^{n-1}} + … = \frac{u_{1}}{1-q} = \frac{-1}{1 – (-\frac{1}{10})} = \frac{-10}{11}\).
6. Giải bài 6 trang 122 sgk Đại số và Giải tích 11
Cho số thập phân vô hạn tuần hoàn \(a = 1, 020 020 …\) (chu kì là \(02\)). Hãy viết a dưới dạng một phân số.
Bài giải:
Ta có \(a = 1, 020 020 … = 1+ \frac{2}{100} + \frac{2}{100^{2}} + …+ \frac{2}{100^{n}}+ …\)
\(= 1 + \frac{\frac{2}{100}}{1-\frac{1}{100}}=1 + \frac{2}{99}=\frac{101}{99}.\)
Vì \(\frac{2}{100}\), \(\frac{2}{100^{2}}\), …, \(\frac{2}{100^{n}}\), … là một cấp số nhân lùi vô hạn có: \(u_1=\frac{2}{100}\), q = \(\frac{1}{100}\).
7. Giải bài 7 trang 122 sgk Đại số và Giải tích 11
Tính các giới hạn sau:
a) \(\lim({n^3} + {\rm{ }}2{n^2}-{\rm{ }}n{\rm{ }} + {\rm{ }}1)\);
b) \(\lim{\rm{ }}( – {n^2} + {\rm{ }}5n{\rm{ }}-{\rm{ }}2)\);
c) \(\lim (\sqrt{n^{2}-n}- n)\);
d) \(\lim (\sqrt{n^{2}-n} + n)\).
Bài giải:
Ta có:
a) \(\lim({n^3} + {\rm{ }}2{n^2}-{\rm{ }}n{\rm{ }} + {\rm{ }}1)= \lim n^3(1 + \frac{2}{n}-\frac{1}{n^{2}}+\frac{1}{n^{3}}) = +∞\)
b) \(\lim{\rm{ }}( – {n^2} + {\rm{ }}5n{\rm{ }}-{\rm{ }}2) = \lim n^2 ( -1 + \frac{5}{n}-\frac{2}{n^{2}}) = -∞\)
c) \(\lim (\sqrt{n^{2}-n} – n) = \lim \frac{(\sqrt{n^{2}-n}-n)(\sqrt{n^{2}-n}+n)}{\sqrt{n^{2}-n}+n}\)
\(= \lim \frac{n^{2}-n-n^{2}}{\sqrt{n^{2}-n}+n} = \lim \frac{-n}{\sqrt{{n^2}\left( {1 – {1 \over n}} \right)}+ n} = \lim \frac{-1}{\sqrt{1-\frac{1}{n}}+1} = \frac{-1}{2}\).
d) \(\lim (\sqrt{n^{2}-n} + n) = \lim \left( {\sqrt {{n^2}\left( {1 – {1 \over n}} \right)} + n} \right) \)
\(= \lim n.\left( {\sqrt {1 – {1 \over n}} + 1} \right)= +∞\).
8. Giải bài 8 trang 122 sgk Đại số và Giải tích 11
Cho hai dãy số \((u_n)\) và \((v_n)\). Biết \(\lim u_n= 3\), \(\lim v_n= +∞\).
Tính các giới hạn:
a) \(\lim \frac{3u_{n}-1}{u_{n}+ 1};\)
b) \(\lim \frac{v_{n}+ 2}{v^{2}_{n}-1}\).
Bài giải:
Ta có:
a) \(\lim \frac{3u_{n}-1}{u_{n}+ 1}= \frac{3.3-1}{3+ 1} = 2\);
b) \(\lim \frac{v_{n}+ 2}{v^{2}_{n}-1}= \frac{\frac{1}{v_{n}}+\frac{2}{v^{2}_{n}}}{1-\frac{1}{v^{2}_{n}}} = 0\).
Bài trước:
Bài tiếp theo:
Xem thêm:
- Các bài toán 11 khác
- Để học tốt môn Vật lí lớp 11
- Để học tốt môn Sinh học lớp 11
- Để học tốt môn Ngữ văn lớp 11
- Để học tốt môn Lịch sử lớp 11
- Để học tốt môn Địa lí lớp 11
- Để học tốt môn Tiếng Anh lớp 11
- Để học tốt môn Tiếng Anh lớp 11 thí điểm
- Để học tốt môn Tin học lớp 11
- Để học tốt môn GDCD lớp 11
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 11 với giải bài 1 2 3 4 5 6 7 8 trang 121 122 sgk Đại số và Giải tích 11!
“Bài tập nào khó đã có giaibaisgk.com“
