Giải bài 1 2 3 4 5 6 7 8 trang 168 169 sgk Đại số và Giải tích 11

Nội Dung

Hướng dẫn giải Bài §3. Đạo hàm của hàm số lượng giác, Chương V. Đạo hàm, sách giáo khoa Đại số và Giải tích 11. Nội dung bài giải bài 1 2 3 4 5 6 7 8 trang 168 169 sgk Đại số và Giải tích 11 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập đại số và giải tích có trong SGK để giúp các em học sinh học tốt môn toán lớp 11.

Lý thuyết

1. Đạo hàm của hàm số $y = sinx$

Hàm số $y=sin x$ có đạo hàm tại mọi $x \in \mathbb{R}$ và $\left( {\sin x} \right)’ = \cos x.$

Nếu $y=sin u$ và $u=u(x)$ thì $(sin u)’=u’. \cos u.$

2. Đạo hàm của hàm số $y = cosx$

Hàm số $y=\cos x$ có đạo hàm tại mọi $x \in \mathbb{R}$ và $\left( {\cos x} \right)’ =-\sin x.$

Nếu $y=\cos u$ và $u=u(x)$ thì $(cos u)’=-u’. \sin u.$

3. Đạo hàm của hàm số $y = tanx$

Hàm số $y=\tan x$ có đạo hàm tại mọi $x \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{R}$ và $\left( {\tan x} \right)’ = \frac{1}{{{{\cos }^2}x}}.$

Nếu $y=tan u$ và $u=u(x)$ thì $\left( {\tan u} \right)’ = \frac{{u’}}{{{{\cos }^2}u}}.$

4. Đạo hàm của hàm số $y = cotx$

Hàm số $y=\cot x$ có đạo hàm tại mọi $x \ne k\pi ,k \in \mathbb{R}$ và $\left( {\cot x} \right)’ = – \frac{1}{{{{\sin }^2}x}}.$

Nếu $y=\cot u$ và $u=u(x)$ thì $\left( {\cot x} \right)’ = – \frac{{u’}}{{{{\sin }^2}u}}$.

Bảng đạo hàm:

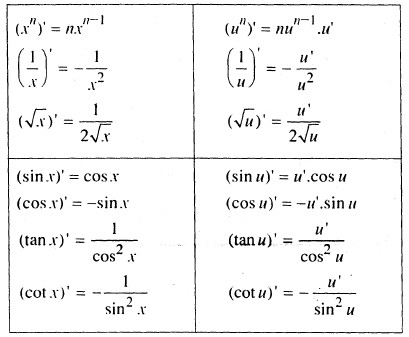
Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong phần hoạt động của học sinh sgk Đại số và Giải tích 11.

Câu hỏi

1. Trả lời câu hỏi 1 trang 163 sgk Đại số và Giải tích 11

Tính ${{\sin 0,01} \over {0,01}};\,\,{{\sin \,0,001} \over {0,001}}$ bằng máy tính bỏ túi.

Trả lời:

Ta có:

$\eqalign{
& {{\sin 0,01} \over {0,01}} \approx 0,999983 \cr
& {{\sin \,0,001} \over {0,001}} \approx 0,99999983 \cr} $

2. Trả lời câu hỏi 2 trang 165 sgk Đại số và Giải tích 11

Tính đạo hàm của hàm số: $y = \sin ({\pi \over 2} – x)$

Trả lời:

$y’ = (sin⁡ ({\pi \over 2} – x) )’$

Đặt $u = {\pi \over 2} – x$ thì $u’ = -1$

⇒ $y’ = u’ cos⁡u = -1 cos⁡({\pi \over 2} – x) = -sin⁡x$

(do $cos⁡({\pi \over 2} – x) = sin⁡x$ ).

3. Trả lời câu hỏi 3 trang 166 sgk Đại số và Giải tích 11

Tính đạo hàm của hàm số:

$f(x) = {{\sin \,x} \over {\cos \,x}}\,(x \ne {\pi \over 2} + k\pi ;\,k \in Z)$

Trả lời:

Ta có:

$\eqalign{
& f'(x) = ({{\sin \,x} \over {\cos \,x}}) ‘= {{(\sin \,x)’\cos \,x – \sin \,x.(\cos \,x)’} \over {\cos {\,^2}x}} \cr
& = {{\cos {\,^2}x + {{\sin }^2}x} \over {\cos {\,^2}x}} = {1 \over {\cos {\,^2}x}} \cr} $

4. Trả lời câu hỏi 4 trang 167 sgk Đại số và Giải tích 11

Tính đạo hàm của hàm số:

$y = tan ({\pi \over 2} – x)$ với $x ≠ kπ, k ∈ Z$

Trả lời:

Đặt $u = {\pi \over 2} – x$ thì $u’ = -1$

⇒ $y’ = {{u’} \over {{{\cos }^2}u}} = {{ – 1} \over {{{\cos }^2}u}} $

$= {{ – 1} \over {{{\cos }^2}({\pi \over 2} – x)}} = {{ – 1} \over {{{\sin }^2}x}}$

(do $cos⁡({\pi \over 2} – x) = sin⁡x$)

Dưới đây là phần Hướng dẫn giải bài 1 2 3 4 5 6 7 8 trang 168 169 sgk Đại số và Giải tích 11. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập đại số và giải tích 11 kèm bài giải chi tiết bài 1 2 3 4 5 6 7 8 trang 168 169 sgk Đại số và Giải tích 11 của Bài §3. Đạo hàm của hàm số lượng giác trong Chương V. Đạo hàm cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 6 7 8 trang 168 169 sgk Đại số và Giải tích 11

1. Giải bài 1 trang 168 sgk Đại số và Giải tích 11

Tìm đạo hàm của các hàm số sau:

a) $y = \frac{x-1}{5x-2}$

b) $y = \frac{2x+3}{7-3x}$

c) $y = \frac{x^{2}+2x+3}{3-4x}$

d) $y = \frac{x^{2}+7x+3}{x^{2}-3x}$

Bài giải:

a) $y = \frac{x-1}{5x-2}$

$ y’=\frac{\left ( x-1 \right )’.\left ( 5x-2 \right )-\left ( x-1 \right ).\left ( 5x-2 \right )’}{\left ( 5x-2 \right )^{2}}$

$y’ =\frac{(5x-2)-\left ( x-1 \right ).5}{\left ( 5x-2 \right )^{2}}$

$y’ =\frac{3}{\left ( 5x-2 \right )^{2}}$.

b) $y = \frac{2x+3}{7-3x}$

$ y’=\frac{\left ( 2x+3 \right )’.\left ( 7-3x \right )-\left ( 2x+3 \right ).\left ( 7-3x \right )’}{\left ( 7-3x \right )^{2}}$

$y’= \frac{2\left ( 7-3x \right )-\left ( 2x+3 \right ).\left ( -3 \right )}{\left ( 7-3x \right )^{2}}$

$y’= \frac{23}{\left ( 7-3x \right )^{2}}$.

c) $y = \frac{x^{2}+2x+3}{3-4x}$

$ y’=\frac{\left ( x^{2}+2x+3 \right )’.\left ( 3-4x \right )-\left ( x^{2} +2x+3\right ).\left ( 3-4x \right )’}{\left ( 3-4x \right )^{2}}$

$y’= \frac{\left ( 2x+2 \right ).\left ( 3-4x \right )-\left ( x^{2}+2x+3 \right ).(-4)}{(3-4x)^{2}}$

$y’ =\frac{-2(2x^{2}-3x-9)}{(3-4x)^{2}}$.

d) $y = \frac{x^{2}+7x+3}{x^{2}-3x}$

$ y’=\frac{(x^{2}+7x+3)’.(x^{2}-3x)-(x^{2}+7x+3).(x^{2}-3x)’}{(x^{2}-3x)^{2}}$

$y’ =\frac{(2x-7).(x^{2}-3x)-(x^{2}+7x+3).(2x-3)}{(x^{2}-3x)^{2}}$

$y’=\frac{-10x^{2}-6x+9}{(x^{2}-3x)^{2}}$.

2. Giải bài 2 trang 168 sgk Đại số và Giải tích 11

Giải các bất phương trình sau:

a) $y'<0$ với ${{{x^2} + x + 2} \over {x – 1}}$

b) $y’≥0$ với $y = \frac{x^{2}+3}{x+1}$

c) $y’>0$ với $y = \frac{2x-1}{x^{2}+x+4}$

Bài giải:

a) $y'<0$ với ${{{x^2} + x + 2} \over {x – 1}}$

Ta có $ y’=\frac{(x^{2}+x+2)’.(x-1)-(x^{2}+x+2).(x-1)’}{(x-1)^{2}}=\frac{x^{2}-2x-3}{(x-1)^{2}}$

$\Rightarrow y'<0\Leftrightarrow \frac{x^{2}-2x-3}{(x-1)^{2}}$

$ \Leftrightarrow \left\{ \matrix{x \ne 1 \hfill \cr – 1 < x < 3 \hfill \cr} \right.$

$\Rightarrow x∈ (-1;1) ∪ (1;3)$

Vậy $x∈ (-1;1) ∪ (1;3)$

b) $y’≥0$ với $y = \frac{x^{2}+3}{x+1}$

Ta có $ y’=\frac{(x^{2}+3)’.(x+1)-(x^{2}+3).(x+1)’}{(x+1)^{2}}= \frac{x^{2}+2x-3}{(x+1)^{2}}$.

$\Rightarrow y’≥0 \Leftrightarrow \frac{x^{2}+2x-3}{(x+1)^{2}}≥0 $

$ \Leftrightarrow \left\{ \matrix{x \ne – 1 \hfill \cr \left[ \matrix{x \ge 1 \hfill \cr
x \le – 3 \hfill \cr} \right. \hfill \cr} \right.$

$\Leftrightarrow \left[ \matrix{x \ge 1 \hfill \cr x \le – 3 \hfill \cr} \right.$

$\Rightarrow x∈ (-∞;-3] ∪ [1;+∞)$

Vậy $x∈ (-∞;-3] ∪ [1;+∞)$

c) $y’>0$ với $y = \frac{2x-1}{x^{2}+x+4}$

Ta có $y’=\frac{(2x-1)’.(x^{2}+x+4)-(2x-1).(x^{2}+x+4)’}{(x^2+x+4)}=\frac{-2x^{2}+2x+9}{(x^{2}+x+4)}$.

Vì $x^2+x +4 =\left ( x+\frac{1}{2} \right )^{2}+ \frac{15}{4} >0$, với $∀ x ∈ \mathbb R$

$\Rightarrow y’>0 \Leftrightarrow \frac{-2x^{2}+2x+9}{(x^{2}+x+4)} >0$

$\Leftrightarrow -2x^2+2x +9>0 $

$\Leftrightarrow \frac{1-\sqrt{19}}{2} < x < \frac{1+\sqrt{19}}{2}$

$\Leftrightarrow x∈ \left ( \frac{1-\sqrt{19}}{2};\frac{1+\sqrt{19}}{2} \right )$

Vậy $x∈ \left ( \frac{1-\sqrt{19}}{2};\frac{1+\sqrt{19}}{2} \right )$

3. Giải bài 3 trang 169 sgk Đại số và Giải tích 11

Tìm đạo hàm của các hàm số sau:

a) $y = 5sinx -3cosx$

b) $ y=\frac{sinx+cosx}{sinx-cosx}$

c) $y = x cotx$

d) $y = \frac{sinx}{x}+\frac{x}{sinx}$

e) $y = \sqrt{(1 +2tan x)}$

f) $y = sin\sqrt{(1 +x^2)}$

Bài giải:

a) $y = 5sinx -3cosx$

$y’=5cosx-3(-sinx)=5cosx+3sinx$

b) $ y=\frac{sinx+cosx}{sinx-cosx}$

$y’={{(sinx+cos x)’.(sin x- cos x)-(sin x+cos x)(sin x-cos x)’}\over{(sin x-cos x)^{2}}}$

$y’= {{(cos x-sin x)(sin x -cos x)-(sin x+ cos x)(cosx+sinx)}\over{(sin x-cosx )^{2}}}$

$y’ ={{-2}\over{(sin x-cos x)^{2}}}$

c) $y = x cotx$

$y’ = cotx +x. \left ( -\frac{1}{sin^{2}x} \right )= cotx – \frac{x}{sin^{2}x}$.

d) $y = \frac{sinx}{x}+ \frac{x}{sinx}$

$ y’=\frac{(sin x)’.x-sin x.(x)’}{x^{2}}+\frac{(x)’.sin x-x(sin x)’}{sin^{2}x}$

$y’= \frac{x.cosx-sinx}{x^{2}}+\frac{sin x-x.cosx}{sin^{2}x}$

$y’= \frac{x.cosx-sinx}{x^{2}}-\frac{x.cosx-sin x}{sin^{2}x}$

$y’ = (x. cosx -sinx) \left ( \frac{1}{x^{2}}-\frac{1}{sin^{2}x} \right )$.

e) $y = \sqrt{(1 +2tan x)}$

$ y’=\frac{(1+2tanx)’}{2\sqrt{1+2tanx}}$

$y’= \frac{\frac{2}{cos^{2}x}}{2\sqrt{1+2tanx}}$

$y’=\frac{1}{cos^{2}x\sqrt{1+2tanx}}$.

f) $y = sin\sqrt{(1 +x^2)}$

$y’ = (\sqrt{1+x^2})’ cos\sqrt{(1+x^2)} $

$y’= \frac{(1+x^{2})’}{2\sqrt{1+x^{2}}}cos\sqrt{(1+x^2)} $

$y’= \frac{2x}{2\sqrt{1+x^{2}}}cos\sqrt{(1+x^2)} $

$y’= \frac{x}{\sqrt{1+x^{2}}}cos\sqrt{(1+x^2)}$

4. Giải bài 4 trang 169 sgk Đại số và Giải tích 11

Tìm đạo hàm của các hàm số sau:

a) $y = \left( {9 – 2x} \right)(2{x^3} – 9{x^2} + 1)$

b) $y = \left ( 6\sqrt{x} -\frac{1}{x^{2}}\right )(7x -3)$

c) $y = (x -2)\sqrt{(x^2+1)}$

d) $y = tan^2x +cotx^2$

e) $y = cos\frac{x}{1+x}$

Bài giải:

a) $y = \left( {9 – 2x} \right)(2{x^3} – 9{x^2} + 1)$

$y’ = \left( {9 – 2x} \right)'(2{x^3} – 9{x^2} + 1) + \left( {9 – 2x} \right)(2{x^3} – 9{x^2} + 1)’$

$y’= – 2(2{x^3} – 9{x^2} + 1) + \left( {9 – 2x} \right)(6{x^2} – 18x) $

$y’=-4x^3+18x^2-2+54x^2-162x-12x^3+36x^2$

$y’= – 16{x^3} + 108{x^2} – 162x – 2$.

b) $y = \left ( 6\sqrt{x} -\frac{1}{x^{2}}\right )(7x -3)$

$y’ = \left ( 6\sqrt{x} -\frac{1}{x^{2}}\right )’.(7x -3) +\left ( 6\sqrt{x} -\frac{1}{x^{2}}\right )(7x -3)’$

$y’= \left ( \frac{3}{\sqrt{x}} +\frac{2}{x^{3}}\right )(7x -3) +7 \left ( 6\sqrt{x} -\frac{1}{x^{2}}\right )$

$y’=63\sqrt{x}-\frac{9}{\sqrt{x}}+\frac{7}{x^2}-\frac{6}{x^3}$

c) $y = (x -2)\sqrt{(x^2+1)}$

$y’ = (x -2)’\sqrt{(x^2+1)} + (x -2)\sqrt {(x^2+1)}’ $

$y’= \sqrt {(x^2+1)} + (x -2)\frac{\left ( x^{2}+1 \right )’}{2\sqrt{x^{2}+1}}$

$y’= \sqrt {(x^2+1)} + (x -2) \frac{2x}{2\sqrt{x^{2}+1}}$

$y’ = \sqrt {(x^2+1)} + \frac{x^{2}-2x}{\sqrt{x^{2}+1}}$

$y’= \frac{2x^{2}-2x+1}{\sqrt{x^{2}+1}}$.

d) $y = tan^2x +cotx^2$

$y’ = 2tanx.(tanx)’ – (x^2)’ \left ( -\frac{1}{sin^{2}x^{2}} \right )= \frac{2tanx}{cos^{2}x}+\frac{2x}{sin^{2}x^{2}}$

e) $y = cos\frac{x}{1+x}$

$y’ = \left ( \frac{1}{1+x} \right )’sin \frac{x}{1+x}= -\frac{1}{(1+x)^{2}}sin \frac{x}{1+x}$.

5. Giải bài 5 trang 169 sgk Đại số và Giải tích 11

Tính $ \frac{f'(1)}{\varphi ‘(1)}$, biết rằng $f(x) = x^2$ và $φ(x) = 4x +sin \frac{\pi x}{2}$

Bài giải:

Ta có:

$f'(x) = 2x\Rightarrow f'(1) = 2$

$φ'(x) = 4 + \left ( \frac{\pi x}{2} \right )’. cos \frac{\pi x}{2} = 4 + \frac{\pi }{2}. cos \frac{\pi x}{2}$

$\Rightarrow φ'(1) = 4$.

$\Rightarrow \frac{f'(1)}{\varphi ‘(1)} = \frac{2}{4}= \frac{1}{2}$

6. Giải bài 6 trang 169 sgk Đại số và Giải tích 11

Chứng minh rằng các hàm số sau có đạo hàm không phụ thuộc $x$:

a) $\sin^6x + \cos^6x + 3\sin^2x.\cos^2x$

b) ${\cos ^2}\left ( \frac{\pi }{3}-x \right )+ {\cos ^2} \left ( \frac{\pi }{3}+x \right ) + {\cos ^2}\left ( \frac{2\pi }{3}-x \right )+{\cos ^2} \left ( \frac{2\pi }{3}+x \right )-2\sin^2x$

Bài giải:

a) $\sin^6x + \cos^6x + 3\sin^2x.\cos^2x$

Ta có:

$(3\sin^2x.\cos^2x)’=3.(sin^2x)’.cos^2x+3.sin^2x(cos^2x)’$

$=3.cos^2x.2.sin x (sin x)’+3.sin^2x.2.cos x.(cosx)’$

$=6.cos^2x.sin x.cos x+6.sin^2x.cos x.(-sin x)$

$=6.cos^3x.sin x-6.sin^3x.cos x$

$y’ = 6{\sin ^5}x.\cos x – 6{\cos ^5}x.\sin x + 6\sin x.\cos^3x – 6{\sin ^3}x.\cos x$

$= 6{\sin ^3}x.\cos x(\sin^2 x – 1) + 6\sin x.\cos^3 x(1 – {\cos ^2}x)$

$= 6{\sin ^3}x.\cos x.cos^2x + 6\sin x.\cos^3 x.sin^2x$

$= – 6{\sin ^3}x.\cos^3 x + 6{\sin ^3}x.\cos^3 x = 0$.

Vậy $y’ = 0$với mọi $x$,tức là $y’$ không phụ thuộc vào $x$.

b) ${\cos ^2}\left ( \frac{\pi }{3}-x \right )+ {\cos ^2} \left ( \frac{\pi }{3}+x \right ) + {\cos ^2}\left ( \frac{2\pi }{3}-x \right )+{\cos ^2} \left ( \frac{2\pi }{3}+x \right )-2\sin^2x$

$y’ = 2cos \left ( \frac{\pi }{3}-x \right ).sin \left ( \frac{\pi }{3}-x \right )$

$ -2cos \left ( \frac{\pi }{3}+x \right ).sin \left ( \frac{\pi }{3}+x \right )$

$ +2cos \left ( \frac{2 \pi }{3}-x \right ).sin \left ( \frac{2 \pi }{3}-x \right )$

$ -2cos \left ( \frac{2 \pi }{3}+x \right ).sin \left ( \frac{2 \pi }{3}+x \right )-4sin\,xcos\,x$

Áp dụng công thức tính đạo hàm của hàm số hợp ta được

$y’ =\sin \left ( \frac{2\pi }{3}-2x \right ) – \sin \left ( \frac{2\pi }{3}+2x \right )+ \sin \left ( \frac{4\pi }{3}-2x \right ) – \sin \left ( \frac{4\pi }{3}+2x \right )- 2\sin 2x $

$= -2\cos \frac{2\pi }{3}.\sin\,2x – 2\cos \frac{4\pi }{3}. \sin 2x – 2\sin 2x $

$= \sin 2x + \sin 2x – 2\sin 2x $

$=sin\,2x(1+1-2)=0$

Vậy $y’ = 0$ với mọi $x$, do đó $y’$ không phụ thuộc vào $x$.

7. Giải bài 7 trang 169 sgk Đại số và Giải tích 11

Giải phương trình $f'(x) = 0$, biết rằng:

a) $f(x) = 3\cos x + 4\sin x + 5x$

b) $f(x) = 1 – \sin(π + x) + 2\cos \left ( \frac{2\pi +x}{2} \right )$

Bài giải:

a) $f(x) = 3\cos x + 4\sin x + 5x$

$f'(x) = – 3\sin x + 4\cos x + 5$.

$\Rightarrow f'(x) = 0 \Leftrightarrow – 3\sin x + 4\cos x + 5 = 0$

$\Leftrightarrow3 \sin x – 4\cos x = 5$

$\Leftrightarrow \frac{3}{5}\sin x – \frac{4}{5}\ cos x = 1$.(*)

Đặt $\cos \alpha = \frac{3}{5},\left(\alpha ∈ \left ( 0;\frac{\pi }{2} \right )\right ) \Rightarrow \sin \alpha = \frac{4}{5}$

Ta có:

(*)$\Leftrightarrow \sin x.\cos \alpha – \cos x.\sin \alpha = 1$

$\Leftrightarrow \sin(x – \alpha ) = 1$

$\Leftrightarrow x – \alpha = \frac{\pi }{2} + k2π$

$\Leftrightarrow x = \alpha + \frac{\pi }{2} + k2π, k ∈ \mathbb Z$.

Vậy $x = \alpha + \frac{\pi }{2} + k2π, k ∈ \mathbb Z$

b) $f(x) = 1 – \sin(π + x) + 2\cos \left ( \frac{2\pi +x}{2} \right )$

$f'(x) = – \cos(π + x) – \sin \left (\pi + \frac{x}{2} \right ) = \cos x + \sin \frac{x }{2}$

$f'(x) = 0 \Leftrightarrow \cos x + \sin \frac{x }{2} = 0 $

$\Leftrightarrow \sin \frac{x }{2} = – cosx$

$\Leftrightarrow sin \frac{x }{2} = sin \left (x-\frac{\pi}{2}\right )$

$\Leftrightarrow \left[ \matrix{\frac{x }{2}= x-\frac{\pi}{2}+ k2π \hfill \cr \frac{x }{2} = π – x+\frac{\pi}{2}+ k2π \hfill \cr} \right.$

$\Leftrightarrow \left[ \matrix{x = π – k4π \hfill \cr x = π + k \frac{4\pi }{3} \hfill \cr} \right.(k ∈ \mathbb Z)$

Vậy $x = π – k4π$hoặc $x = π + k \frac{4\pi }{3}(k ∈ \mathbb Z)$

8. Giải bài 8 trang 169 sgk Đại số và Giải tích 11

Giải bất phương trình $f'(x) > g'(x)$, biết rằng:

a) $f(x) = x^3+ x – \sqrt2\,g(x) = 3x^2+ x + \sqrt2$

b) $f(x) = 2x^3- x^2+ \sqrt3,g(x) = x^3+ \frac{x^{2}}{2} – \sqrt 3$

Bài giải:

a) $f(x) = x^3+ x – \sqrt2\,g(x) = 3x^2+ x + \sqrt2$

Ta có $f'(x) = 3x^2+ 1$, $g'(x) = 6x + 1$.

$\Rightarrow f'(x) > g'(x) $

$\Rightarrow 3x^2+ 1 > 6x + 1 $

$\Leftrightarrow 3x^2- 6x >0$

$\Leftrightarrow 3x(x – 2) > 0 $

$\Leftrightarrow x > 2$hoặc $x > 0$

Vậy $x ∈ (-∞;0) ∪ (2;+∞)$.

b) $f(x) = 2x^3- x^2+ \sqrt3,g(x) = x^3+ \frac{x^{2}}{2} – \sqrt 3$

Ta có $f'(x) = 6x^2- 2x$, $g'(x) = 3x^2+ x$.

$\Rightarrow f'(x) > g'(x)$

$\Leftrightarrow 6x^2- 2x > 3x^2+ x $

$\Leftrightarrow 3x^2- 3x > 0$

$\Leftrightarrow 3x(x – 1) > 0 $

$\Leftrightarrow x > 1$hoặc $x < 0$

Vậy $ x ∈ (-∞;0) ∪ (1;+∞)$.

Bài trước:

Giải bài 1 2 3 4 5 trang 162 163 sgk Đại số và Giải tích 11

Bài tiếp theo:

Giải bài 1 2 trang 171 sgk Đại số và Giải tích 11

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 11 với giải bài 1 2 3 4 5 6 7 8 trang 168 169 sgk Đại số và Giải tích 11!

“Bài tập nào khó đã có giaibaisgk.com“