Hướng dẫn Giải bài 1 2 3 4 5 6 7 trang 140 sgk Đại số 10

Nội Dung

Hướng dẫn giải Bài §1. Cung và góc lượng giác, Chương VI – Cung và góc lượng giác. Công thức lượng giác, sách giáo khoa Đại số 10. Nội dung bài giải bài 1 2 3 4 5 6 7 trang 140 sgk Đại số 10 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập phần đại số có trong SGK để giúp các em học sinh học tốt môn toán lớp 10.

Lý thuyết

1. Độ và rađian

a) Độ

Độ là số đo của góc bằng ${1 \over {180}}$ góc bẹt.

Số đo của mộtcung tròn bằng số đo của góc ở tâm chắn cung đo.

Như vậy số đo của cung bằng ${1 \over {180}}$ nửa đường tròn là một độ.

Kí hiệu $1^0$ đọc là một độ.

$1^0= 60’$; $1′ = 60”$

b) Radian

Cung có độ dài bằng bán kính đường tròn chứa cung ấy có số đo là $1$ radian, kí hiệu $1rad $ hay đơn giản là bỏ chữ $rad$ và kí hiệu là $1$.

c) Quan hệ giữa độ và radian

${180^0} = \pi rad \Rightarrow {1^0} = {\pi \over {180}}rad,1rad = {\left( {{{180} \over \pi }} \right)^0}$

d) Độ dài cung tròn

Một cung của đường tròn bán kính $R$ có số đo $a^0$ (số đo $α rad$) thì độ dài $l = {{\pi R\alpha } \over {180}}$ (hay $l = Rα$).

2. Góc và cung lượng giác

a) Góc lượng giác

Trên mặt phẳng, quay tia $Ox$ quanh $O$ đến tia $Oy$ theo một chiều nhất định thì có một góc lượng giác, kí hiệu $(Ox; Oy)$. Tia $Ox$ là tia đầu (tia gốc, $Oy$ là tia cuối (tia ngọn). Quy ước chiều ngược kim đồng hồ là chiều dương.

Hai góc lượng giác có cùng tia đầu và tia cuối thì có các số đo khác nhau một bội nguyên $360^0$ (hay $2π$).

b) Cung lượng giác

Trên đường tròn định hướng tâm $O$ lấy hai điểm $A, B$. Một điểm chạy trên đường tròn theo một chiều nhất định từ $A$ đến $B$ vạch nên cung lượng giác, kí hiệu cung $AB$. Điểm $A$ là điểm đầu, $B$ là điểm cuối. Số đo cung $AB$ kí hiệu sđ bằng sđ $(OA, OB)$.

Hai cung lượng giác có cùng điểm đầu và điểm cuối thì có số đo khác nhau bội $360^0$ (hay $2π$).

3. Hệ thức Salơ

Ba tia chung gốc $OA, OB, OC$ bất kì thì:

$sđ(OA, OB) + sđ(OB, OC) = sđ(OA, OC) + k.360^0$ $(k2π)$

4. Biểu diễn cung lượng giác trên đường tròn lượng giác

a) Đường tròn lượng giác là đường tròn định hướng có tâm là gốc $O$ của hệ toạ độ trực chuẩn có bán kính bằng 1. Điểm gốc của cung lượng giác là điểm $A (1; 0)$

b) Biểu diễn cung lượng giác trên đường tròn lượng giác có số đo bằng $α$ bằng cách chọn điểm gốc là điểm $A(1;0)$ là điểm ngọn $M$ sao cho sđ cung $AM$ bằng $α$.

Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong phần hoạt động của học sinh sgk Đại số 10.

Câu hỏi

1. Trả lời câu hỏi 1 trang 136 sgk Đại số 10

Sử dụng máy tính bỏ túi để đổi từ độ sang radian và ngược lại.

a) Đổi 35^o47’25’’ sang radian

b) Đổi 3 rad ra độ

Trả lời:

a) Đổi 35^o47’25’’ sang radian

Nếu dùng máy tính CASIO fx-500MS ta làm như sau:

cho kết quả 0.6247 (đã làm tròn đến bốn chữ số thập phân)

b) Đổi 3 rad ra độ

Nếu dùng máy tính CASIO fx-500MS ta làm như sau:

cho kết quả 171^o53’14” (đã làm tròn đến giây).

2. Trả lời câu hỏi 2 trang 138 sgk Đại số 10

Cung lượng giác $\overparen{AD}$ (h.45) có số đo là bao nhiêu ?

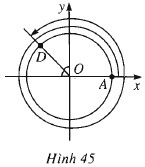
Trả lời:

Cung lượng giác $\overparen{AD}$ có số đo là:

$2π +$ $ \frac{π}{2}$ + $ \frac{π}{4}$ = $ \frac{11π}{4}$

3. Trả lời câu hỏi 3 trang 139 sgk Đại số 10

Tìm số đo của các góc lượng giác $(OA, OE)$ và $(OA, OP)$ trên hình 46 (điểm E là điểm chính giữa của cung $\overparen{A’B’}$, $\overparen{AP}$ = $ \frac{1}{3}$ $\overparen{AB}$). Viết số đo này theo đơn vị radian và theo đơn vị độ.

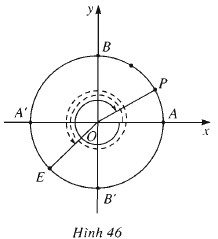
Trả lời:

Số đo của góc lượng giác (OA, OE) = sđ $\overparen{AE}$= sđ $\overparen{AB’}$ + sđ $\overparen{B’E}$ = (- 90^o ) + (-45^o ) = -135^o

Số đo của góc lượng giác (OA, OP) = sđ $\overparen{AP}$ = $ \frac{1}{3}$ $\overparen{AB}$ = 30^o.

Dưới đây là phần Hướng dẫn giải bài 1 2 3 4 5 6 7 trang 140 sgk Đại số 10. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập phần đại số 10 kèm bài giải chi tiết bài 1 2 3 4 5 6 7 trang 140 sgk Đại số 10 của Bài §1. Cung và góc lượng giác trong Chương VI – Cung và góc lượng giác. Công thức lượng giác cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 6 7 trang 140 sgk Đại số 10

1. Giải bài 1 trang 140 sgk Đại số 10

Khi biểu diễn các cung lượng giác có số đo khác nhau trên đường tròn lượng giác, có thể xảy ra trường hợp các điểm cuối của chúng trùng nhau không? Khi nào trường hợp này xảy ra?

Trả lời:

Khi số đo hai cung lệch nhau $k2\pi (k \in \mathbb{Z})$ thì điểm cuối của chúng có thể trùng nhau.

2. Giải bài 2 trang 140 sgk Đại số 10

Đổi số đo của các góc sau đây ra rađian:

a) $18^0$	b) $57^030’$
c) $-25^0$	d) $-125^045’$

Bài giải:

Ta có:

a) $ 18^0 = \frac{\pi .18}{180} = \frac{\pi }{10}\,rad$

b) $57^030 = 57,5^0 = \frac{\pi .57,5}{180} = 1,0036\,rad$

c) $-25^0 = \frac{-25.\pi }{180} = -0,4363\,rad$

d) $-125^045’ = \frac{\pi .(-125,75)}{180} = -2,1948\,rad$

3. Giải bài 3 trang 140 sgk Đại số 10

Đổi số đo của các sau đây ra độ, phút, giây:

a) $ \frac{\pi}{18}$	b) $ \frac{3\pi}{16}$
c) $-2$	d) $ \frac{3}{4}$

Bài giải:

Ta có:

a) $ \frac{\pi}{18}rad = \left ( \frac{\pi }{18}.\frac{180}{\pi } \right )^0 = 10^0$

b) $ \frac{3\pi}{16}rad = \left ( \frac{3\pi}{16}.\frac{180}{\pi } \right )^0 = 33^045’$

c) $-2rad = \left ( -2.\frac{180}{\pi } \right )^0\approx -114^035’30’’$

d) $ \frac{3}{4}rad = \left ( \frac{3}{4}.\frac{180}{\pi } \right )^0 = 42^058’19”$

4. Giải bài 4 trang 140 sgk Đại số 10

Một đường tròn có bán kính $20 cm$. Tìm độ dài của các cung trên đường tròn đó có số đo:

a) $ \frac{\pi }{15}$

b) $1,5$

c) $37^0$

Bài giải:

Từ công thức $l=R.\alpha $

Ta có:

$\begin{array}{l}
a)\;l = 20.\frac{\pi }{{15}} \approx 4,19\;cm.\\
b)\;l = 20.1,5 = 30\;cm.\\
c)\;l = \frac{{20.\pi {{.37}^0}}}{{{{180}^0}}} \simeq 12,92\;cm.
\end{array}$

5. Giải bài 5 trang 140 sgk Đại số 10

Trên đường tròn lượng giác hãy biểu diễn các cung có số đo

a) $- {{5\pi } \over 4}$	b) $135^0$
c) ${{10\pi } \over 3}$	d) $-225^0$

Bài giải:

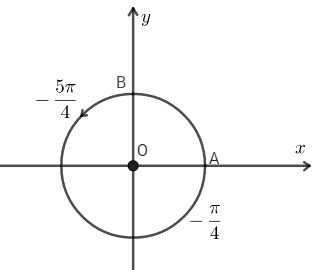
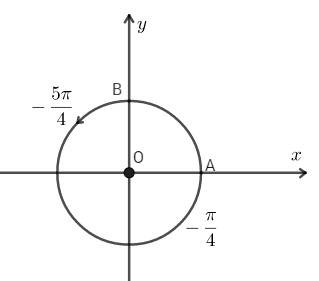
a) Cung $- {{5\pi } \over 4}$

Cách vẽ:

– Vẽ cung $-\frac{\pi }{4}$

– Đi theo chiều âm, đếm đủ $5$ cung.

– Ta có điểm cuối.

b) Cung $135^0$

Cách vẽ:

– Vẽ cung $45^0$

– Đi theo chiều dương kể từ điểm $A$, đếm đủ $3$ cung.

– Ta có điểm cuối.

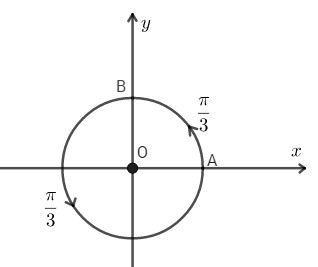
c) Cung ${{10\pi } \over 3}$

Cách vẽ:

– Vẽ cung $\frac{\pi }{3}$

– Đi theo chiều dương kể từ điểm $A$, đếm đủ $10$ cung.

– Ta có điểm cuối.

d) Cung $-225^0$

Cách vẽ: Ta thấy $-225^0=-\frac{5\pi }{4}$

⇒ Vẽ tương tự câu a).

6. Giải bài 6 trang 140 sgk Đại số 10

Trên đường tròn lượng giác gốc $A$, xác định các điểm $M$ khác nhau, biết rằng cung $AM$ có số đo tương ứng là (trong đó $k$ là một số nguyên tuỳ ý)

a) $kπ$

b) $k{\pi \over 2}$

c) $k{\pi \over 3}$

Bài giải:

a) Với $k=1$ ta có $\overparen{AM}= \pi \Rightarrow {M_1}\left( {1;\;0} \right).$

Với $k=-1$ ta có $ \overparen{AM}= -\pi \Rightarrow {M_2}\left( {-1;\;0} \right).$

Vậy ta có các điểm $M_1(1; 0), M_2(-1; 0)$

b) Tương tự câu a với các giá trị $k = \left\{ { – 2;\; – 1;\;1;\;2} \right\}$ ta tìm được các điểm ${M_1}(1;0),{M_2}(0;1),{M_3}( – 1;0),$${M_4}(0; – 1).$

c) Tương tự câu a với các giá trị $k = \left\{ { -6; \,-3; \,- 2;\; – 1;\;1;\;2; \,3; \, 6} \right\}$ ta được các điểm ${M_1}(1;0),{M_2}\left( {{1 \over 2};{{\sqrt 3 } \over 2}} \right),{M_3}\left( { – {1 \over 2};{{\sqrt 3 } \over 2}} \right),$

${M_4}( – 1;0),{M_5}\left( { – {1 \over 2}; – {{\sqrt 3 } \over 2}} \right),$${M_6}\left( {{1 \over 2}; – {{\sqrt 3 } \over 2}} \right)$

7. Giải bài 7 trang 140 sgk Đại số 10

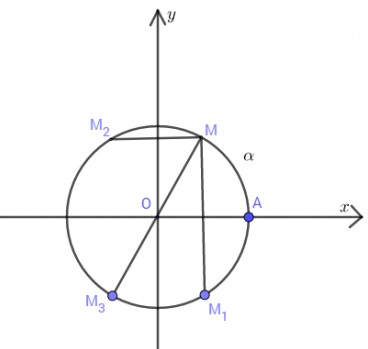
Trên đường tròn lượng giác cho điểm $M$ xác định bởi $sđ\overparen{AM} = α (0 < α < {\pi \over 2})$

Gọi $M_1, M_2, M_3$ lần lượt là điểm đối xứng của $M$ qua trục $Ox, Oy$ và gốc toạ độ. Tìm số đo các cung $\overparen{AM_1}, \overparen{AM_2} , \overparen{AM_3}$ .

Bài giải:

Theo đề bài ta có:

$sđ\overparen{AM} = \alpha \left ( 0< \alpha < \frac{\pi }{2} \right )\Rightarrow \overparen{AM}=\alpha $

Nên ta có với $k \in \mathbb{Z}$

$sđ\overparen{AM_1} = – α + k2π, k\in\mathbb Z$

$sđ\overparen{AM_2} = π – α + k2π, k\in\mathbb Z$

$sđ\overparen{AM_3} = π + α + k2π, k\in\mathbb Z$

Bài tiếp theo:

Giải bài 1 2 3 4 5 trang 148 sgk Đại số 10

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 10 với giải bài 1 2 3 4 5 6 7 trang 140 sgk Đại số 10!

“Bài tập nào khó đã có giaibaisgk.com“

a) \(18^0\)	b) \(57^030’\)
c) \(-25^0\)	d) \(-125^045’\)

a) \( \frac{\pi}{18}\)	b) \( \frac{3\pi}{16}\)
c) \(-2\)	d) \( \frac{3}{4}\)

a) \(- {{5\pi } \over 4}\)	b) \(135^0\)
c) \({{10\pi } \over 3}\)	d) \(-225^0\)