Hướng dẫn Giải bài 1 2 3 4 5 6 7 trang 156 157 sgk Đại số và Giải tích 11

Nội Dung

Hướng dẫn giải Bài §1. Định nghĩa và ý nghĩa của đạo hàm, Chương V. Đạo hàm, sách giáo khoa Đại số và Giải tích 11. Nội dung bài giải bài 1 2 3 4 5 6 7 trang 156 157 sgk Đại số và Giải tích 11 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập đại số và giải tích có trong SGK để giúp các em học sinh học tốt môn toán lớp 11.

Lý thuyết

1. Định nghĩa đạo hàm

Cho hàm số $y = f(x)$ xác định trên khoảng $(a;b)$, $x_0\in (a;b)$. Giới hạn hữu hạn (nếu có) của tỉ số $\frac{f(x)-f(x_{0})}{x-x_{0}}$ khi $x → x_0$ được gọi là đạo hàm của hàm số đã cho tại $x_0$, kí hiệu là $f'( x_0)$ hay $y'( x_0)$. Như vậy:

$f'( x_0) = \lim_{x\rightarrow x_{0}}$ $ \frac{f(x)-f(x_{0})}{x-x_{0}}$.

Nếu đặt $x – x_0= ∆x$ và $∆y = f(x_0+∆x) – f(x_0)$ thì ta có

$f'(x_0) = \lim_{\Delta x\rightarrow 0}$ $ \frac{\Delta y}{\Delta x}$

Đại lượng $∆x$ được gọi là số gia của đối số tại $x_0$ và đại lượng $∆y$ được gọi là số gia tương ứng của hàm số.

2. Quy tắc tính đạo hàm bằng định nghĩa

– Bước 1. Với $∆x$ là số gia của số đối tại $x_0$ ,tính $∆y = f(x_0+∆x)- f(x_0)$;

– Bước 2. Lập tỉ số $ \frac{\Delta y}{\Delta x}$;

– Bước 3. Tính $ \lim_{\Delta x\rightarrow 0}$ $ \frac{\Delta y}{\Delta x}$.

Nhận xét: nếu thay $x_0$ bởi $x$ ta có định nghĩa và quy tắc tính đạo hàm của hàm số $y = f(x)$ tại điểm $x ∈ (a;b)$.

3. Quan hệ giữa tính liên tục và sự tồn tại đạo hàm

Định lí: Nếu hàm số $y = f(x)$ có đạo hàm tại $x_0$ thì nó liên tục tại $x_0$_.

Chú ý:

Định lí trên tương đương với khẳng định : Nếu $y = f(x)$ gián đoạn tại $x_0$ thì nó không có đạo hàm tại điểm đó.

Mệnh đề đảo của định lí không đúng. Một hàm số liên tục tại một điểm có thể không có đạo hàm tại điểm đó.

4. Ý nghĩa hình học của đạo hàm

Nếu tồn tại, $f'(x_0)$ là hệ số góc của tiếp tuyến của đồ thị hàm số $y = f(x)$ tại điểm $M_0(x_0;f(x_0))$. Khi đó phương trình tiếp tuyến của đồ thị tại điểm $M_0(x_0;f(x_0))$ là:

$ y – f(x_0) = f'(x_0)(x-x_0)$

Các bước viết phương trình tiếp tuyến của đồ thị (C) tại điểm $M_0(x_0;y_0) \in (C):$

Bước 1: Tính $f'({x_0}) = \mathop {\lim }\limits_{ x \to x_0} \frac{{f(x) – f({x_0})}}{{x – {x_0}}}= \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f({x_0} + \Delta x) – f({x_0})}}{{x – {x_0}}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}}.$

– Bước 2: Hệ số góc của tiếp tuyến với đồ thị (C) tại $M_0$ là $k=f'(x_0)$

– Bước 3: Phương trình tiếp tuyến với đồ thị (C) tại điểm $M_0(x_0;y_0) \in (C)$ là: $y = f'({x_0}).(x – {x_0}) + {y_0}$

Các bước viết phương trình tiếp tuyến của đồ thị (C) hàm số y=f(x) khi biết hệ số k:

– Bước 1: Gọi $M_0(x_0;y_0) \in (C)$ là tiếp điểm của tiếp tuyến với đồ thị (C).

– Bước 2: Tính $f'({x_0}) = \mathop {\lim }\limits_{ x \to x_0} \frac{{f(x) – f({x_0})}}{{x – {x_0}}}= \mathop {\lim }\limits_{\Delta x \to 0} \frac{{f({x_0} + \Delta x) – f({x_0})}}{{x – {x_0}}} = \mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}}.$

– Bước 3: Giải phương trình $k=f'(x_0)$ tìm $x_0$, rồi tìm $y_0=f(x_0).$

– Bước 4: Phương trình tiếp tuyến của đồ thị (C) với hệ số góc k là: $y = k(x – {x_0}) + {y_0}.$

5. Ý nghĩa vật lí của đạo hàm

Vận tốc tức thời của chuyển động thẳng xác định bởi phương trình: $s=s(t)$ tại thời điểm $t_0$ là $v(t_0)=s'(t_0).$

Cường độ tức thời của điện lượng $Q=Q(t)$ tại thời điểm $t_0$ là: $I(t_0)=Q'(t_0).$

Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong phần hoạt động của học sinh sgk Đại số và Giải tích 11.

Câu hỏi

1. Trả lời câu hỏi 1 trang 146 sgk Đại số và Giải tích 11

Một đoàn tàu chuyển động khởi hành từ một nhà ga. Quãng đường $s$ (mét) đi được của đoàn tàu là một hàm số của thời gian $t$ (phút). Ở những phút đầu tiên, hàm số đó là $s = t^2$.

Hãy tính vận tốc trung bình của chuyển động trong khoảng [t; t_o] với t_o $= 3$ và $t = 2; t = 2,5; t = 2,9; t = 2,99.$

Nêu nhận xét về những kết quả thu được khi $t$ càng gần t_o $= 3$.

Trả lời:

Vận tốc của đoàn tàu là:

$v = {s \over t} = {{{t^2}} \over t} = t$

Vận tốc trung bình của chuyển động trong khoảng [t; t_o] với:

$\eqalign{
& {t_0} = 3;\,t = 2:\,\,{{3 + 2} \over 2} = 2,5 \cr
& {t_0} = 3;\,t = 2,5:\,{{3 + 2,5} \over 2} = 2,75 \cr
& {t_0} = 3;\,t = 2,9:\,\,{{3 + 2,9} \over 2} = 2,95 \cr
& {t_0} = 3;\,t = 2,99:\,{{3 + 2,99} \over 2} = 2,995 \cr} $

⇒ $t$ càng gần t_o $= 3$ thì vận tốc trung bình của chuyển động trong khoảng [t; t_o] càng gần $3$.

2. Trả lời câu hỏi 2 trang 149 sgk Đại số và Giải tích 11

Cho hàm số $y = x^2$. Hãy tính $y'(x_0)$ bằng định nghĩa.

Trả lời:

Ta có:

$\eqalign{
& y'({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} {{{x^2} – {x_0}^2} \over {x – {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} {{(x – {x_0})(x + {x_0})} \over {x – {x_0}}} \cr
& = \mathop {\lim }\limits_{x \to {x_0}} (x + {x_0}) = 2{x_0} \cr} $

3. Trả lời câu hỏi 3 trang 150 sgk Đại số và Giải tích 11

a) Vẽ đồ thị của hàm số $f(x) = {{{x^2}} \over 2}$

b) Tính $f’(1)$.

c) Vẽ đường thẳng đi qua điểm $M(1; {1 \over 2})$ và có hệ số góc bằng $f’(1)$. Nêu nhận xét về vị trí tương đối của đường thẳng này và đồ thị hàm số đã cho.

Trả lời:

a) Vẽ đồ thị của hàm số $f(x) = {{{x^2}} \over 2}$

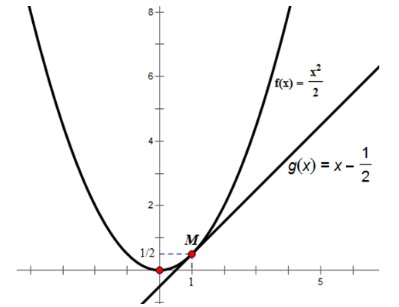
b) Giả sử $Δx$ là số gia của đối số tại x_o $= 1$. Ta có:

$\eqalign{
& \Delta y = f(1 + \Delta x) – f(1) = {{{{(1 + \Delta x)}^2}} \over 2} – {{{1^2}} \over 2} = {{{{(\Delta x)}^2} + 2\Delta x} \over 2} \cr
& \Rightarrow {{\Delta y} \over {\Delta x}} = {{{{(\Delta x)}^2} + 2\Delta x} \over 2}:\Delta x = {{\Delta x} \over 2} + 1 \cr
& \Rightarrow f'(1) = \mathop {\lim }\limits_{\Delta x \to 0} {{\Delta y} \over {\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} {{\Delta x} \over 2} + 1 = 0 + 1 = 1 \cr} $

c) Đường thẳng có hệ số góc bằng $f'(1) = 1$ có dạng:

$y = 1.x + a$ hay $y = x + a$

Mà đường thẳng đó đi qua điểm $M(1; {1 \over 2})$ nên có:

${1 \over 2}$ = 1 + a ⇒ a = ${1 \over 2}$ – 1 = -${1 \over 2}$

⇒ đường thẳng đi qua $M$ và có hệ số góc bằng $1$ là:

$y = x – {1 \over 2}$

Ta có đồ thị như trên. Đường thẳng $y = x – {1 \over 2}$ tiếp xúc với đồ thị hàm số $f(x)$ tại $M$.

4. Trả lời câu hỏi 4 trang 152 sgk Đại số và Giải tích 11

Viết phương trình đường thẳng đi qua M_o(x_o; y_o) và có hệ số góc $k$.

Trả lời:

Đường thẳng đi qua điểm M_o(x_o; y_o) và có hệ số góc $k$ có phương trình:

$y = k(x – x_0) + y_0$ hay $y = kx + (–kx_0 + y_0)$

5. Trả lời câu hỏi 5 trang 152 sgk Đại số và Giải tích 11

Cho hàm số $y = -x^2 + 3x – 2$. Tính $y’(2)$ bằng định nghĩa.

Trả lời:

Giả sử $Δx$ là số gia của đối số tại $x_0 = 2$. Ta có:

$Δy = y(2 + Δx) – y(2)$

$= -(2 + Δx)^2+ 3(2 + Δx) – 2 – (-2^2 + 3.2 – 2)$

$= -(4 + 4Δx + (Δx)^2)+ 6 + 3Δx – 2 = – (Δx)^2 – Δx$

$\eqalign{
& \Rightarrow {{\Delta y} \over {\Delta x}} = {{ – {{(\Delta x)}^2} – \Delta x} \over {\Delta x}} = – \Delta x – 1 \cr
& \Rightarrow y'(2) = \mathop {\lim }\limits_{\Delta x \to 0} {{\Delta y} \over {\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} ( – \Delta x – 1) = – 1 \cr} $

6. Trả lời câu hỏi 6 trang 153 sgk Đại số và Giải tích 11

Bằng định nghĩa, hãy tính đạo hàm của các hàm số:

a) $f(x) = x^2$ tại điểm $x$ bất kì;

b) $g(x) = {1 \over x}$ tại điểm bất kì $x ≠ 0$.

Trả lời:

a) Giả sử $Δx$ là số gia của đối số tại $x_0$ bất kỳ. Ta có:

$\eqalign{
& \Delta y = f({x_0} + \Delta x) – f({x_0}) \cr
& = {({x_0} + \Delta x)^2} – {x_0}^2 = 2{x_0}\Delta x + {(\Delta x)^2} \cr
& \Rightarrow {{\Delta y} \over {\Delta x}} = {{2{x_0}\Delta x + {{(\Delta x)}^2}} \over {\Delta x}} = 2{x_0} + \Delta x \cr
& \Rightarrow y'({x_0}) = \mathop {\lim }\limits_{\Delta x \to 0} {{\Delta y} \over {\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} (2{x_0} + \Delta x) = 2{x_0} \cr} $

b) Giả sử $Δx$ là số gia của đối số tại $x_0$ bất kỳ. Ta có:

$\eqalign{
& \Delta y = g({x_0} + \Delta x) – g({x_0}) \cr
& = {1 \over {{x_0} + \Delta x}} – {1 \over {{x_0}^2}} = {{ – \Delta x} \over {{x_0}({x_0} + \Delta x)}} \cr
& \Rightarrow {{\Delta y} \over {\Delta x}} = {{ – \Delta x} \over {{x_0}({x_0} + \Delta x)}}:\Delta x = {{ – 1} \over {{x_0}({x_0} + \Delta x)}} \cr
& y'({x_0}) = \mathop {\lim }\limits_{\Delta x \to 0} {{\Delta y} \over {\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} ({{ – 1} \over {{x_0}({x_0} + \Delta x)}}) = {{ – 1} \over {{x_0}^2}} \cr} $

Dưới đây là phần Hướng dẫn giải bài 1 2 3 4 5 6 7 trang 156 157 sgk Đại số và Giải tích 11. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập đại số và giải tích 11 kèm bài giải chi tiết bài 1 2 3 4 5 6 7 trang 156 157 sgk Đại số và Giải tích 11 của Bài §1. Định nghĩa và ý nghĩa của đạo hàm trong Chương V. Đạo hàm cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 6 7 trang 156 157 sgk Đại số và Giải tích 11

1. Giải bài 1 trang 156 sgk Đại số và Giải tích 11

Tìm số gia của hàm số $f(x) = x^3$, biết rằng :

a) $x_0 = 1; ∆x = 1$;

b) $x_0= 1; ∆x = -0,1$.

Bài giải:

a) $∆y = f(x_0+∆x) – f(x_0) = f(1+1)-f(1)$

$=f(2) – f(1) = 2^3-1^3= 7$.

b) $∆y = f(x_0+∆x) – f(x_0) = f(1-0,1)-f(1)=f(0,9) – f(1)$

$= \left ( \frac{9}{10} \right )^{3} – 1^3= \frac{729}{1000} – 1 = -\frac{271}{1000}=-0,271$.

2. Giải bài 2 trang 156 sgk Đại số và Giải tích 11

Tính $∆y$ và ${{\Delta y} \over {\Delta x}}$ của các hàm số sau theo $x$ và $∆x$ :

a) $y = 2x – 5$; b) $y = x^2- 1$;

c) $y = 2x^3$; d) $y = {1 \over x}$.

Bài giải:

a) $∆y = f(x+∆x) – f(x) $=$ 2(x+∆x) – 5 – (2x – 5)$

$= 2x+2∆x-5-2x+5=2∆x$

${{\Delta y} \over {\Delta x}} = {{2\Delta x} \over {\Delta x}} = 2$.

b) $\Delta y = f(\Delta x + x) – f(x)$

$= {(x + \Delta x)^2} – 1 – ({x^2} – 1)$

$=x^2+2x.∆x+(∆x)^2-1-x^2+1$

$= 2x.\Delta x + {(\Delta x)^2}$

$= \Delta x(2x + \Delta x)$

${{\Delta y} \over {\Delta x}} = {{\Delta x\left( {2x + \Delta x} \right)} \over {\Delta x}} = 2x+\Delta x$

c) $∆y = f(x+∆x) – f(x) = 2(x + ∆x)^3- 2x^3$

$=2\left [ x^3+3x^2.∆x+3.x(∆x)^2+(∆x)^3 \right ]-2x^3$

$= 2x^3+6x^2.∆x+6.x(∆x)^2+2(∆x)^3 -2x^3$

$=6{x^2}\Delta x + 6x{(\Delta x)^2} + 2{(\Delta x)^3}$

$= 2\Delta x.\left [ 3{x^2} + 3x\Delta x + {(\Delta x)^2} \right ]$

$\frac{\Delta y}{\Delta x} = \frac{2\Delta x\left [ 3x^2+3x\Delta x+(\Delta x)^2 \right ]}{\Delta x}= 6x^2+ 6x∆x + 2(∆x)^2$

d) $∆y = f(x+∆x) – f(x) =-{1 \over x} + {1 \over {x +\Delta x}} = {{-x – \Delta x + x} \over {x\left( {x + \Delta x} \right)}} = – {{\Delta x} \over {x\left( {x + \Delta x} \right)}}$

${{\Delta y} \over {\Delta x}} = \frac{- {{\Delta x} \over {x\left( {x + \Delta x} \right)}}}{\Delta x}=-{1 \over {\left( {x + \Delta x} \right)x}}$

3. Giải bài 3 trang 156 sgk Đại số và Giải tích 11

Tính (bằng định nghĩa) đạo hàm của mỗi hàm số sau tại các điểm đã chỉ ra:

a) $y = x^2+ x$ tại $x_0= 1$;

b) $y = \frac{1}{x}$ tại $x_0= 2$;

c) $y = \frac{x+1}{x-1}$ tại $x_0 = 0$.

Bài giải:

a) Giả sử $∆x$ là số gia của số đối tại $x_0 = 1$.

Ta có: $∆y = f(1 + ∆x) – f(1) $

$= (1 + ∆x)^2+ (1 + ∆x) – (1^2+ 1)= 3∆x + (∆x)^2$

$\frac{\Delta y}{\Delta x} = \frac{3∆x + (∆x)^2}{∆x}=3 + ∆x$

$\mathop {\lim }\limits_{\Delta x \to 0} {{\Delta y} \over {\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} (3 + \Delta x) = 3$

Vậy $f'(1) = 3$.

b) Giả sử $∆x$ là số gia của số đối tại $x_0= 2$

Ta có: $∆y = f(2 + ∆x) – f(2)$

$= \frac{1}{2+\Delta x} – \frac{1}{2} =\frac{2-2-\Delta x}{2(2+\Delta x)}= – \frac{\Delta x}{2\left ( 2+\Delta x \right )}$;

$ \frac{\Delta y}{\Delta x} = \frac{- \frac{\Delta x}{2\left ( 2+\Delta x \right )}}{\Delta x}=- \frac{1}{2\left ( 2+\Delta x \right )}$

$\mathop {\lim }\limits_{\Delta x \to 0} {{\Delta y} \over {\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \left( { – {1 \over {2.(2 + \Delta x)}}} \right) = – {1 \over 4}$

Vậy $f'(2) = – \frac{1}{4}$.

c) Giả sử $∆x$ là số gia của số đối tại $x_0= 0$.

Ta có: $∆y = f(∆x) – f(0) = \frac{\Delta x+1}{\Delta x-1}- ( -1) =\frac{∆x+1+∆x-1}{∆x-1}= \frac{2\Delta x}{\Delta x-1}$;

$ \frac{\Delta y}{\Delta x}=\frac{\frac{2\Delta x}{\Delta x-1}}{∆x}=\frac{2}{\Delta x-1}$

$ \mathop {\lim}\limits_{\Delta x\rightarrow 0}$ $ \frac{\Delta y}{\Delta x}$ = $ \mathop {\lim}\limits_{\Delta x\rightarrow 0}$ $ \frac{2}{\Delta x-1} = -2$.

Vậy $f'(0) = -2$.

4. Giải bài 4 trang 156 sgk Đại số và Giải tích 11

Chứng minh rằng hàm số

$f(x) = \left\{ \matrix{
{(x – 1)^2}\text{ nếu }x \ge 0 \hfill \cr
– {x^2}\text { nếu } x < 0 \hfill \cr} \right.$

không có đạo hàm tại điểm $x = 0$ nhưng có đạo hàm tại điểm $x = 2$.

Bài giải:

Ta có:

$ \mathop{\lim}\limits_{x\rightarrow 0^{+}} f(x) =\mathop{\lim}\limits_{x\rightarrow 0^{+}} (x – 1)^2= 1$

$ \mathop{\lim}\limits_{x\rightarrow 0^{-}} f(x) = \mathop{ \lim}\limits_{x\rightarrow 0^{-}} (-x^2) = 0$.

Vì $ \mathop{\lim}\limits_{x\rightarrow 0^{+}} f(x)\neq \mathop{\lim}\limits_{x\rightarrow 0^{-}} f(x)$

$\Rightarrow $hàm số $y = f(x)$gián đoạn tại $x = 0$

Vậy hàm số không có đạo hàm tại điểm $x = 0$.

Ta có:

$\mathop{ \lim}\limits_{\Delta x\rightarrow 0}\frac{f\left ( 2+\Delta x \right )-f\left ( 2 \right )}{\Delta x}$

$=\mathop{\lim}\limits_{\Delta x\rightarrow 0} \frac{\left ( 1+\Delta x \right )^{2}-1^{2}}{\Delta x}$

$ =\mathop{\lim}\limits_{\Delta x\rightarrow 0} (2 + ∆x) = 2$.

Vậy hàm số $y = f(x)$ có đạo hàm tại $x = 2$, khi đó $f'(2) = 2$.

5. Giải bài 5 trang 156 sgk Đại số và Giải tích 11

Viết phương trình tiếp tuyến của đường cong $y = x^3$:

a) Tại điểm có tọa độ $(-1;-1)$;

b) Tại điểm có hoành độ bằng $2$;

c) Biết hệ số góc của tiếp tuyến bằng $3$

Bài giải:

Bằng định nghĩa ta tính được $y’ = 3x^2$.

a) Tại điểm có tọa độ $(-1;-1)$

$y’ (-1) = 3$.

Vậy hệ số góc của tiếp tuyến bằng $3$.

Vậy phương trình tiếp tuyến tại điểm $(-1;-1)$ là

$y – (-1) = 3[x – (-1)]$ hay $y = 3x+2$.

b) Tại điểm có hoành độ bằng $2$

$y’ (2) = 12$.

Vậy hệ số góc của tiếp tuyến bằng $12$

Ta lại có $y(2) = 8$.

Vậy phương trình tiếp tuyến tại điểm có hoành độ bằng $2$ là: $ y – 8 = 12(x – 2)$ hay $y = 12x -16$.

c) Biết hệ số góc của tiếp tuyến bằng $3$

Gọi $x_0$ là hoành độ tiếp điểm. Ta có:

$y’ (x_0) = 3 \Leftrightarrow 3{x_0}^2= 3\Leftrightarrow {x_0}^2= 1\Leftrightarrow x_0= ±1$.

Với $x_0= 1$ ta có $y(1) = 1$, phương trình tiếp tuyến là $ y – 1 = 3(x – 1)$ hay $y = 3x – 2$.

Với $x_0= -1$ ta có $y(-1) = -1$, phương trình tiếp tuyến là $y – (-1) = 3[x – (-1)]$ hay $y = 3x + 2$.

6. Giải bài 6 trang 156 sgk Đại số và Giải tích 11

Viết phương trình tiếp tuyến của đường hypebol $y = \frac{1}{x}$:

a) Tại điểm $( \frac{1}{2} ; 2)$

b) Tại điểm có hoành độ bằng $-1$;

c) Biết rằng hệ số góc của tiếp tuyến bằng -$ \frac{1}{4}$.

Bài giải:

Bằng định nghĩa ta tính được $y’ = – \frac{1}{x^{2}}$.

a) Tại điểm $( \frac{1}{2} ; 2)$:

$y’ \left ( \frac{1}{2} \right )= -4$.

Vậy hệ số góc của tiếp tuyến bằng $-4$.

Vậy phương trình tiếp tuyến của hypebol tại điểm $( \frac{1}{2} ; 2)$ là $y – 2 = -4(x – \frac{1}{2})$ hay $y = -4x + 4$.

b) Tại điểm có hoành độ bằng $-1$:

$y’ (-1) = -1$.

Vậy hệ số góc của tiếp tuyến bằng $-1$.

Ta lại có $y(-1) = -1$.

Vậy phương trình tiếp tuyến tại điểm có tọa độ là $-1$ là $y – (-1) = -[x – (-1)]$ hay $y = -x – 2$.

c) Biết hệ số góc của tiếp tuyến bằng -$ \frac{1}{4}$:

Gọi $x_0$ là hoành độ tiếp điểm.

Ta có $y’ (x_0) = – \frac{1}{4} \Leftrightarrow – \frac{1}{x_{0}^{2}} = – \frac{1}{4}$$\Leftrightarrow x_{0}^{2} = 4 \Leftrightarrow x_{0}= ±2$.

Với $x_{0}= 2$ ta có $y(2) = \frac{1}{2}$, phương trình tiếp tuyến là $y – \frac{1}{2} = – \frac{1}{4}(x – 2)$ hay $y = -\frac{1}{4}x + 1$.

Với $x_{0} = -2$ ta có $y (-2) = – \frac{1}{2}$, phương trình tiếp tuyến là $y – \left ( -\frac{1}{2} \right ) = – \frac{1}{4}[x – (-2)]$ hay $y = – \frac{1}{4}x -1$.

7. Giải bài 7 trang 157 sgk Đại số và Giải tích 11

Một vật rơi tự do theo phương trình $s = {1 \over 2}g{t^2}$ , trong đó $g ≈ 9,8$ m/s² là gia tốc trọng trường.

a) Tìm vận tốc trung bình của chuyển động trong khoảng thời gian từ t (t = 5s) đến $t + ∆t$, trong các trường hợp $∆t = 0,1s; ∆t = 0,05s; ∆t = 0,001s$.

b) Tìm vận tốc tức thời của chuyển động tại thời điểm $t = 5s$

Bài giải:

a) Vận tốc trung bình của chuyển động trong khoảng thời gian từ $t$ đến $t + ∆t$ là:

$V_{tb}= \frac{s\left ( t+\Delta t \right )-s\left ( t \right )}{\Delta t}= \frac{\frac{1}{2}g\cdot \left ( t+\Delta t \right )^{2}-\frac{1}{2}g\cdot t^{2}}{\Delta t} ={1 \over 2}g(2t + \Delta t) \approx 4,9.(2t + \Delta t)$

Với $ t=5$ và:

$∆t = 0,1$ thì $v_{tb}≈ 4,9. (10 + 0,1) ≈ 49,49 m/s$;

$∆t = 0,05$ thì $v_{tb}≈ 4,9. (10 + 0,05) ≈ 49,245 m/s$;

$∆t = 0,001$ thì $v_{tb} ≈ 4,9. (10 + 0,001) ≈ 49,005 m/s$.

b) Vận tốc tức thời của chuyển động tại thời điểm $t = 5s$ tương ứng với $∆t = 0$

Vậy $v ≈ 4,9 . 10 = 49 m/s$.

Bài trước:

Ôn tập chương IV: Giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 trang 141 142 143 144 sgk Đại số và Giải tích 11

Bài tiếp theo:

Giải bài 1 2 3 4 5 trang 162 163 sgk Đại số và Giải tích 11

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 11 với giải bài 1 2 3 4 5 6 7 trang 156 157 sgk Đại số và Giải tích 11!

“Bài tập nào khó đã có giaibaisgk.com“