Hướng dẫn Giải bài 1 2 3 4 5 6 trang 140 141 sgk Đại số và Giải tích 11

Nội Dung

Hướng dẫn giải Bài §3. Hàm số liên tục, Chương IV. Giới hạn, sách giáo khoa Đại số và Giải tích 11. Nội dung bài giải bài 1 2 3 4 5 6 trang 140 141 sgk Đại số và Giải tích 11 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập đại số và giải tích có trong SGK để giúp các em học sinh học tốt môn toán lớp 11.

Lý thuyết

1. Định nghĩa

Cho hàm số $y = f(x)$ xác định trên khoảng K và ${x_0} \in K$

Hàm số $y = f(x)$ liên tục tại ${x_0} \Leftrightarrow \mathop {\lim }\limits_{x \to {x_0}} f(x) = f({x_0})$

Hàm số $y = f(x)$ không liên tục tại ${x_0}$ ta nói hàm số gián đoạn tại ${x_0}$

Hàm số $y = f(x)$ liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.

Hàm số $y = f(x)$ liên tục trên đoạn $\left[ {a;b} \right]$ nếu nó liên tục trên $\left( {a;b} \right)$ và

$\mathop {\lim }\limits_{x \to {a^ + }} f(x) = f(a)$, $\mathop {\lim }\limits_{x \to {b^ – }} f(x) = f(b)$.

2. Một số định lí cơ bản

Định lí 1:

a) Hàm số đa thức liên tục trên tập R.

b) Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng.

Định lí 2:

Các hàm số $y = f(x),{\rm{ }}y = g(x)$ liên tục tại ${x_0}$. Khi đó tổng, hiệu, tích liên tục tai x₀, thương $y = \frac{{f(x)}}{{g(x)}}$ liên tục nếu $g({x_0}) \ne 0$.

Định lí 3:

Cho hàm số f liên tục trên đoạn $\left[ {a;b} \right]$.

Nếu $f(a) \ne f(b)$ và M là một số nằm giữa $f(a){\rm{ }},f(b)$ thì tồn tại ít nhất một số $c \in \left( {a;b} \right)$ sao cho $f(c) = M{\rm{ }}$

Hệ quả:

Cho hàm số f liên tục trên đoạn $\left[ {a;b} \right]$.

Nếu $f(a){\rm{ }}f(b) < 0$ thì tồn tại ít nhất một số $c \in \left( {a;b} \right)$ sao cho $f(c) = 0$.

Chú ý: Ta có thể phát biểu hệ quả trên theo cách khác như sau :

Cho hàm số f liên tục trên đoạn $\left[ {a;b} \right]$. Nếu $f(a){\rm{ }}f(b) < 0$ thì phương trình $f(x) = 0$ có ít nhất một nghiệm thuộc $(a;b)$.

Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong phần hoạt động của học sinh sgk Đại số và Giải tích 11.

Câu hỏi

1. Trả lời câu hỏi 1 trang 135 sgk Đại số và Giải tích 11

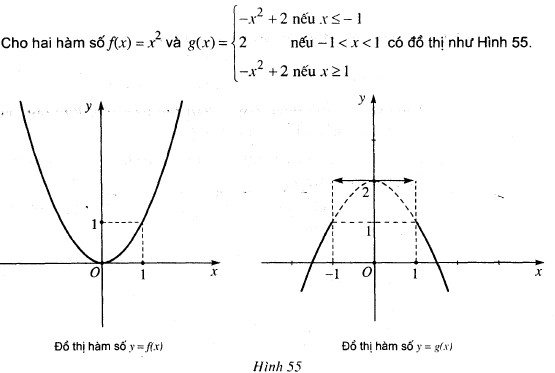
a) Tính giá trị của mỗi hàm số tại x = 1 và so sánh với giới hạn (nếu có) của hàm số đó khi x → 1;

b) Nêu nhận xét về đồ thị của mỗi hàm số tại điểm có hoành độ x = 1.

Trả lời:

a) Ta có: $f(1) = {1^2} = 1 = \mathop {\lim }\limits_{x \to 1} f(x)$

Vì $x=1$ nên $g(1) =-1^2+ 1 = -1 + 1 = 0$

Lại có: $\mathop {\lim }\limits_{x \to {1^ + }} g\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( { – {x^2} + 2} \right) = 1$ và $\mathop {\lim }\limits_{x \to {1^ – }} g\left( x \right) = \mathop {\lim }\limits_{x \to {1^ – }} \left( 2 \right) = 2$ nên $\mathop {\lim }\limits_{x \to {1^ – }} g\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ + }} g\left( x \right)$ và không tồn tại giới hạn $\mathop {\lim }\limits_{x \to 1} g\left( x \right)$

b) Đồ thị hàm số $f(x)$ liên tục tại $x = 1$

Đồ thị hàm số $g(x) $ gián đoạn tại $x = 1$

2. Trả lời câu hỏi 2 trang 138 sgk Đại số và Giải tích 11

Trong biểu thức xác định $h(x)$ cho ở Ví dụ 2, cần thay số $5$ bởi số nào để được một hàm số mới liên tục trên tập số thực $R$ ?

Trả lời:

Để hàm số liên tục trên $\mathbb{R}$ thì nó phải liên tục tại $x = 1$ hay $\mathop {\lim }\limits_{x \to 1} h\left( x \right) = h\left( 1 \right)$ $ \Leftrightarrow h\left( 1 \right) = 2$.

Vậy cần thay số $5$ bằng số $2$ để hàm số liên tục trên $\mathbb{R}$.

3. Trả lời câu hỏi 3 trang 138 sgk Đại số và Giải tích 11

Giả sử hàm số $y = f(x)$ liên tục trên đoạn $[a; b]$ với $f(a)$ và $f(b)$ trái dấu nhau.

Hỏi đồ thị của hàm số có cắt trục hoành tại điểm thuộc khoảng $(a; b)$ không?

⦁ Bạn Hưng trả lời rằng: “Đồ thị của hàm số $y = f(x)$ phải cắt trục hoành $Ox$ tại một điểm duy nhất nằm trong khoảng $(a; b)$”.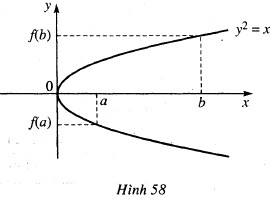

⦁ Bạn Lan khẳng định: “Đồ thị của hàm số $y = f(x)$ phải cắt trục hoành $Ox$ ít nhất tại một điểm nằm khoảng $(a; b)$”.

⦁ Bạn Tuấn thì cho rằng: “Đồ thị của hàm số $y = f(x)$ có thể không cắt trục hoành trong khoảng $(a; b)$, chẳng hạn như đường parabol ở hình (h.58).

Câu trả lời của bạn nào đúng, vì sao?

Trả lời:

⦁ Bạn Lan nói đúng vì $f(a)$ và $f(b)$ trái dấu nên tồn tại ít nhất 1 giá trị $x$ sao cho $f(x) = 0$, do đó đồ thị hàm số $y = f(x)$ cắt trục hoành tại ít nhất 1 điểm.

⦁ Bạn Hưng sai vì có thể có $2$ giá trị $x$ sao cho $f(x) = 0$.

⦁ Đường parabol trên hình 58 là đồ thị hàm số y² = x ⇒ đồ thị hàm số $y = f(x$) sẽ là 1 nửa nằm trên hoặc 1 nửa nằm dưới trục hoành.

Khi đó $f(a)$ và $f(b)$ cùng dấu, mâu thuẫn với điều kiện $f(a)$ và $f(b)$ trái dấu. Ví dụ của Tuấn sai

4. Trả lời câu hỏi 4 trang 139 sgk Đại số và Giải tích 11

Hãy tìm hai số $a$ và $b$ thỏa mãn $1 < a < b < 2$, sao cho phương trình trong Ví dụ 3 ở trên có ít nhất một nghiệm thuộc khoảng $(a; b)$.

Trả lời:

Ta có: $f\left( x \right) = {x^3} + 2x – 5$.

Chọn $a = \dfrac{5}{4},b = \dfrac{7}{4}$ thỏa mãn $1 < a < b < 2$.

Ta thấy: $f\left( {\dfrac{5}{4}} \right) = – \dfrac{{35}}{{64}} < 0,$ $f\left( {\dfrac{7}{4}} \right) = \dfrac{{247}}{{64}} > 0$ nên $f\left( {\dfrac{5}{4}} \right).f\left( {\dfrac{7}{4}} \right) < 0$.

Vậy trong khoảng $\left( {\dfrac{5}{4};\dfrac{7}{4}} \right)$ thì phương trình $f\left( x \right) = 0$ có ít nhất một nghiệm.

Dưới đây là phần Hướng dẫn giải bài 1 2 3 4 5 6 trang 140 141 sgk Đại số và Giải tích 11. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập đại số và giải tích 11 kèm bài giải chi tiết bài 1 2 3 4 5 6 trang 140 141 sgk Đại số và Giải tích 11 của Bài §3. Hàm số liên tục trong Chương IV. Giới hạn cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 6 trang 140 141 sgk Đại số và Giải tích 11

1. Giải bài 1 trang 140 sgk Đại số và Giải tích 11

Dùng định nghĩa xét tính liên tục của hàm số $f(x) = x^3+ 2x – 1$ tại $x_0= 3$.

Bài giải:

Hàm số $f(x) = x_3+ 2x – 1$ xác định trên $\mathbb R$ và $x_0= 3 ∈ \mathbb R$.

$\underset{x\rightarrow 3}{lim} f(x) =$ $\underset{x\rightarrow 3}{lim}( x^3+ 2x – 1) = 3^3+ 2.3 – 1 = f(3)$
nên hàm số đã cho liên tục tại điểm $x_0= 3$.

2. Giải bài 2 trang 141 sgk Đại số và Giải tích 11

a) Xét tính liên tục của hàm số $y = g(x)$ tại $x_0= 2$, biết

$g(x) = \left\{\begin{matrix} \frac{x^{3}-8}{x- 2}; &x\neq 2 \\ 5;& x=2 \end{matrix}\right.$.

b) Trong biểu thức xác định $g(x)$ ở trên, cần thay số $5$ bởi số nào để hàm số liên tục tại $x_0= 2$.

Bài giải:

a) Ta có $\underset{x\rightarrow 2}{\lim} g(x) = $$\underset{x\rightarrow 2}{lim}$ $\frac{x^{3}-8}{x-2}$ = $\underset{x\rightarrow 2}{lim}(x^2+2x + 4) = 2^2+2.2 +4 = 12$.

Vì $\underset{x\rightarrow 2}{\lim} g(x) ≠ g(2)$ nên hàm số $y = g(x)$ gián đoạn tại $x_0= 2$.

b) Để hàm số $y = f(x)$ liên tục tại $x_0= 2$ thì ta cần thay số $5$ bởi số $12$.

3. Giải bài 3 trang 141 sgk Đại số và Giải tích 11

Cho hàm số $f(x) = \left\{\begin{matrix} 3x + 2; & x<-1\\ x^{2}-1 & x \geq -1 \end{matrix}\right.$

a) Vẽ đồ thị của hàm số $y = f(x)$. Từ đó nêu nhận xét về tính liên tục của hàm số trên tập xác định của nó.

b) Khẳng định nhận xét trên bằng một chứng minh.

Bài giải:

a) Khi $x<-1$, đồ thị hàm số là đường thẳng $y=3x+2$, khi $ x \ge -1$ đồ thị hàm số là parabol $y=x^2-1$.

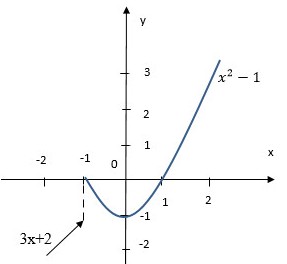
Đồ thị hàm số $y = f(x)$ là một đường không liền nét mà bị đứt quãng tại $x_0= -1$. Vậy hàm số đã cho liên tục trên khoảng $(-∞; -1)$ và $(- 1; +∞)$.

b) Ta có:

Nếu $x < -1$: $f(x) = 3x + 2$ liên tục trên $(-∞; -1)$ (vì đây là hàm đa thức).

Nếu $x> -1$: $f(x) = x^2- 1$ liên tục trên $(-1; +∞)$ (vì đây là hàm đa thức).

Tại $x = -1$; Ta có:

$\underset{x\rightarrow -1^{-}}{lim} f(x) = $$\underset{x\rightarrow -1^{-}}{lim} (3x + 2) = 3(-1) +2 = -1$.

$\underset{x\rightarrow -1^{+}}{lim} f(x) = \underset{x\rightarrow -1^{+}}{lim} (x^2- 1) = (-1)^2- 1 = 0$.

Vì $\underset{x\rightarrow -1^{-}}{lim} f(x) ≠ \underset{x\rightarrow -1^{+}}{lim} f(x)$ nên không tồn tại $\underset{x\rightarrow -1}{lim} f(x)$. Vậy hàm số gián đoạn tại $x_0= -1$.

4. Giải bài 4 trang 141 sgk Đại số và Giải tích 11

Cho hàm số $f(x) = \frac{x +1}{x^{2}+x-6}$ và $g(x) = tanx + sin x$.

Với mỗi hàm số, hãy xác định các khoảng trên đó hàm số liên tục.

Bài giải:

Hàm số $f(x) = \frac{x +1}{x^{2}+x-6}$ xác định khi và chỉ khi $x^2+ x – 6 ≠ 0 \Leftrightarrow x ≠ -3$ và $x ≠ 2$.

Hàm số $f(x)$ liên tục trên các khoảng $(-∞; -3), (-3; 2)$ và $(2; +∞)$

Hàm số $g(x) = tanx + sinx$ xác định khi và chỉ khi $tanx ≠ 0\Leftrightarrow x ≠ \frac{\pi }{2} +kπ$ với $k ∈ Z$.

Hàm số $g(x)$ liên tục trên các khoảng $( – \frac{\pi }{2}+kπ; \frac{\pi }{2}+kπ)$ với $k ∈ \mathbb Z$.

5. Giải bài 5 trang 141 sgk Đại số và Giải tích 11

Ý kiến sau đúng hay sai ?

“Nếu hàm số $y = f(x)$ liên tục tại điểm $x_0$ còn hàm số $y = g(x)$ không liên tục tại $x_0$ thì $y = f(x) + g(x)$ là một hàm số không liên tục tại $x_0$”

Bài giải:

Ý kiến đúng

Giả sử ngược lại $y = f(x) + g(x)$ liên tục tại $x_0$. Đặt $h(x) = f(x) + g(x)$. Ta có $g(x) = h(x) – f(x)$.

Vì $y = h(x)$ và $y = f(x)$ liên tục tại $x_0$ nên hiệu của chúng là hàm số $y = g(x)$ phải liên tục tại $x_0$. Điều này trái với giả thiết là $y = g(x)$ không liên tục tại $x_0$.

6. Giải bài 6 trang 141 sgk Đại số và Giải tích 11

Chứng minh rằng phương trình:

a) $2x^3- 6x + 1 = 0$ có ít nhất hai nghiệm;

b) $cosx = x$ có nghiệm.

Bài giải:

a) Hàm số $fx)=2x^3-6x + 1 = 0$ là hàm đa thức nên liên tục trên $\mathbb R$.

Ta có: $f(0).f(1) = 1.(-3) < 0$ nên phương trình có nghiệm trong khoảng $(0; 1)$.

$f(-2).f(0)=-5<0$ nên phương trình có nghiệm trong khoảng $(-2; 0)$.

Do đó phương trình $f(x) = 0$ có ít nhất hai nghiệm.

b) Hàm số $g(x) = cosx – x$ xác định trên $\mathbb R$ nên liên tục trên $\mathbb R$.

Mặt khác, ta có $g(0).g(\frac{\pi }{2}) = 1. (-\frac{\pi }{2}) < 0$ nên phương trình đã cho có nghiệm trong khoảng $(0; \frac{\pi }{2})$.

Bài trước:

Giải bài 1 2 3 4 5 6 7 trang 132 133 sgk Đại số và Giải tích 11

Bài tiếp theo:

Ôn tập chương IV: Giải bài 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 trang 141 142 143 144 sgk Đại số và Giải tích 11

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 11 với giải bài 1 2 3 4 5 6 trang 140 141 sgk Đại số và Giải tích 11!

“Bài tập nào khó đã có giaibaisgk.com“