Hướng dẫn Giải bài 1 2 3 4 5 6 trang 36 37 sgk Đại số và Giải tích 11

Nội Dung

Hướng dẫn giải Bài §3. Một số phương trình lượng giác thường gặp, Chương I. Hàm số lượng giác và phương trình lượng giác, sách giáo khoa Đại số và Giải tích 11. Nội dung bài giải bài 1 2 3 4 5 6 trang 36 37 sgk Đại số và Giải tích 11 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập đại số và giải tích có trong SGK để giúp các em học sinh học tốt môn toán lớp 11.

Lý thuyết

1. Phương trình bậc nhất với một hàm số lượng giác

Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng $at + b = 0$ trong đó $a, b$ là các hằng số $\left( {a \ne 0} \right)$ và t là một trong các hàm số lượng giác.

Ví dụ: $2\sin x – 1 = 0\,;\,\,\,c{\rm{os}}2x + \frac{1}{2} = 0;\,\,\,3\tan x – 1 = 0;\,\,\sqrt 3 \cot x + 1 = 0$

Phương pháp giải: Đưa về phương trình lượng giác cơ bản.

2. Phương trình bậc hai đối với một hàm số lượng giác

Dạng phương trình:

$\begin{array}{l}a{\sin ^2}x + b\sin x + c = 0\\a{\cos ^2}x + b\cos x + c = 0\\a{\tan ^2}x + b\tan x + c = 0\\a{\cot ^2}x + b\cot x + c = 0\end{array}$

Cách giải:

Đặt: $t = \sin x{\rm{ ( – 1}} \le {\rm{t}} \le {\rm{1)}}$

$\begin{array}{l}t = \cos x{\rm{ ( – 1}} \le {\rm{t}} \le {\rm{1)}}\\t = \tan x\\t = \cot x\end{array}$

Chú ý:

Nếu a là một số cho trước mà $\tan \alpha $ xác định thì phương trình tanx = tana có nghiệm x = $\alpha + $kp thoả điều kiện $\cos x \ne 0$.

Phương trình tanP(x) = tanQ(x) thì cần phải chú ý đến điều kiện cosP(x) $\ne$ 0 và cosQ(x) $\ne$ 0.

3. Phương trình bậc nhất đối với $sinx$ và $cosx$

Dạng phương trình:

$a\sin x + b\cos x = c{\rm{ (1)}}$

Điều kiện có nghiệm: ${a^2} + {b^2} \ge {c^2}$

Cách giải:

♦ Cách 1: Chia hai vế của (1) cho $\sqrt {{a^2} + {b^2}} $, ta được:

$\left( 1 \right) \Leftrightarrow \frac{a}{{\sqrt {{a^2} + {b^2}} }}\sin x + \frac{b}{{\sqrt {{a^2} + {b^2}} }}\cos x = \frac{c}{{\sqrt {{a^2} + {b^2}} }}$

Vì ${\left( {\frac{a}{{\sqrt {{a^2} + {b^2}} }}} \right)^2} + {\left( {\frac{b}{{\sqrt {{a^2} + {b^2}} }}} \right)^2} = 1$ nên ta đặt $\left\{ {\begin{array}{*{20}{c}}{\sin \varphi = \frac{a}{{\sqrt {{a^2} + {b^2}} }}}\\{\cos \varphi = \frac{b}{{\sqrt {{a^2} + {b^2}} }}}\end{array}} \right.$

Phương trình trở thành:

$\sin x\sin \varphi + \cos x\cos \varphi = \frac{c}{{\sqrt {{a^2} + {b^2}} }} \Leftrightarrow \cos \left( {x – \varphi } \right) = \frac{c}{{\sqrt {{a^2} + {b^2}} }}$

Đặt $\cos \alpha = \frac{c}{{\sqrt {{a^2} + {b^2}} }}$ ta được phương trình lượng giác cơ bản.

Hoàn toàn tương tự ta cũng có thể đặt $\left\{ \begin{array}{l}\cos \varphi = \frac{a}{{\sqrt {{a^2} + {b^2}} }}\\\sin \varphi = \frac{b}{{\sqrt {{a^2} + {b^2}} }}\end{array} \right.$

Khi đó phương trình trở thành: ${\mathop{\rm sinxcos}\nolimits} \varphi + cosxsin\varphi = \frac{c}{{\sqrt {{a^2} + {b^2}} }} \Leftrightarrow \sin \left( {x + \varphi } \right) = \frac{c}{{\sqrt {{a^2} + {b^2}} }}$

♦ Cách 2:

Xét $\cos \frac{x}{2} = 0 \Leftrightarrow x = \pi + k2\pi ,{\rm{ k}} \in \mathbb{Z}$ có là nghiệm của (1) không

Xét $\cos \frac{x}{2} \ne 0 \Leftrightarrow x \ne \pi + k2\pi ,k \in \mathbb{Z}$

Đặt $t = \tan \frac{x}{2}$. Khi đó $\sin x = \frac{{2t}}{{1 + {t^2}}}$ và $\cos x = \frac{{1 – {t^2}}}{{1 + {t^2}}}$

Phương trình trở thành:

$a.\frac{{2t}}{{1 + {t^2}}} + b.\frac{{1 – {t^2}}}{{1 + {t^2}}} = c \Leftrightarrow \left( {b + c} \right){t^2} – 2at + c – b = 0{\rm{ (2)}}$

Giải (2) theo t, tìm được t thay vào $t = \tan \frac{x}{2}$ suy ra x

♦ Cách 3:

Nếu $a \ne 0$ chia 2 vế cho a rồi ta đặt $\tan \alpha = \frac{b}{a}$ $\left( { – \frac{\pi }{2} < \alpha < \frac{\pi }{2}} \right)$

Phương trình trở thành: $\sin x + \frac{{\sin \alpha }}{{c{\rm{os}}\alpha }}\cos x = \frac{c}{a}$

$ \Leftrightarrow c{\rm{os}}\alpha \sin x + \sin \alpha \cos x = \frac{c}{a}c{\rm{os}}\alpha \Leftrightarrow \sin (x + \alpha ) = \frac{c}{a}c{\rm{os}}\alpha $

Đặt $\sin \varphi = \frac{c}{a}\cos \alpha $ ta được phương trình lượng giác cơ bản $\sin (x + \alpha ) = \sin \varphi $.

Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong phần hoạt động của học sinh sgk Đại số và Giải tích 11.

Câu hỏi

1. Trả lời câu hỏi 1 trang 29 sgk Đại số và Giải tích 11

Giải các phương trình trong ví dụ 1.

a) $2sinx – 3 = 0$ là phương trình bậc nhất đối với $sinx.$

b) $\sqrt 3 tanx + 1 = 0$ là phương trình bậc nhất đố với $tanx.$

Trả lời:

a) Ta thấy: $2sinx – 3 = 0 ⇔ sin⁡ x = {3 \over 2}$ , vô nghiệm vì $|sin⁡x| ≤ 1$

b) Ta có: $\sqrt 3tan⁡x + 1 = 0 ⇔ tan⁡x = {{ – \sqrt 3 } \over 3}$

$⇔ x = {{ – \pi } \over 6} + kπ, k ∈ Z$

2. Trả lời câu hỏi 2 trang 31 sgk Đại số và Giải tích 11

Giải các phương trình sau:

a) 3cos²x $– 5cosx + 2 = 0$;

b) 3tan²x – 2√3 $tanx + 3 = 0$.

Trả lời:

a) 3cos²x – $5 cos⁡ x + 2 = 0$

Đặt $cos⁡ x = t$ với điều kiện $-1 ≤ t ≤ 1$ (*),

ta được phương trình bậc hai theo $t$:

3t² $- 5t + 2 = 0 (1)$

$Δ =$ (-5)² $- 4.3.2 = 1$

Phương trình (1)có hai nghiệm là:

$\eqalign{
& {t_1} = {{ – ( – 5) + \sqrt 1 } \over {2.3}} = {6 \over 6} = 1\,\,(thỏa\,mãn) \cr
& {t_2} = {{ – ( – 5) – \sqrt 1 } \over {2.3}} = {4 \over 6} = {2 \over 3}\,\,(thỏa\,mãn) \cr} $

Ta có:

$cos⁡ x = 1 ⇔ cos ⁡x = cos⁡ 0$

$⇔ x = k2π, k ∈ Z$

cos⁡x = 2/3 ⇔ x = ± arccos⁡ 2/3 + k2π, k ∈ Z

b) 3tan² x – 2√3 $tan⁡x + 3 = 0$

Đặt $tan⁡x = t$

Ta được phương trình bậc hai theo $t$:

3t² – 2√3 t + 3 = 0(1)

$Δ =$ (-2√3)² $- 4.3.3 = -24 < 0$

Vậy Phương trình (1) vô nghiệm, nên không có $x$ thỏa mãn đề bài.

3. Trả lời câu hỏi 3 trang 32 sgk Đại số và Giải tích 11

Hãy nhắc lại:

a) Các hằng đẳng thức lượng giác cơ bản;

b) Công thức cộng;

c) Công thức nhân đôi;

d) Công thức biến đổi tích thành tổng và tổng thành tích.

Trả lời:

a) Các hằng đẳng thức lượng giác cơ bản:

sin²α + cos²α $= 1$

1 + tan²α = ${1 \over {{{\cos }^2}\alpha }}$; α ≠ ${\pi \over 2}$ + kπ, k ∈ Z

1 + cot²α = ${1 \over {{{\sin }^2}\alpha }}$; α ≠ kπ, k ∈ Z

$tan⁡α.cot⁡α = 1$; α ≠ ${{k\pi } \over 2}$, k ∈ Z

b) Công thức cộng:

$cos⁡(a – b) = cos⁡a cos⁡b + sin⁡a sin⁡b$

$cos⁡(a + b) = cos⁡a cos⁡b – sin⁡a sin⁡b$

$sin⁡(a – b) = sin⁡a cos⁡b – cos⁡a sin⁡b$

$\eqalign{
& \tan (a – b) = {{\tan \,a – \tan \,b} \over {1 + \tan \,a.\tan \,b}} \cr
& \tan (a + b) = {{\tan \,a – \tan \,b} \over {1 – \tan \,a.\tan \,b}} \cr} $

c) Công thức nhân đôi:

$sin⁡2α = 2 sin⁡α cos⁡α$

$cos⁡2α =$ cos²α – sin²α = 2cos²α – 1 = 1 – 2sin²α

$\tan 2\alpha = {{2\tan \alpha } \over {1 – {{\tan }^2}\alpha }}$

d) Công thức biến đổi tích thành tổng:

$cos⁡ a cos⁡b = {1 \over 2} [cos⁡(a – b) + cos⁡(a + b) ]$

$sin⁡a sin⁡b = {1 \over 2} [cos⁡(a – b) – cos⁡(a + b) ]$

$sin⁡a cos⁡b = {1 \over 2} [sin⁡(a – b) + sin⁡(a + b) ]$

Công thức biến đổi tổng thành tích:

$\eqalign{
& \cos u + \cos v = 2\cos {{u + v} \over 2}\cos {{u – v} \over 2} \cr
& \cos u – \cos v = – 2\sin {{u + v} \over 2}\sin {{u – v} \over 2} \cr
& \sin u + \sin v = 2\sin {{u + v} \over 2}\cos {{u – v} \over 2} \cr
& \sin u – \sin v = 2\cos {{u + v} \over 2}\sin {{u – v} \over 2} \cr} $

4. Trả lời câu hỏi 4 trang 34 sgk Đại số và Giải tích 11

Giải phương trình $3cos^2 6x + 8sin3x cos3x – 4 = 0$.

Trả lời:

$3cos^2 6x + 8sin3x cos3x – 4 = 0$.

$⇔ 3(1-sin^2 6x)+ 4sin⁡6x – 4 = 0$

$⇔ -3sin^2 6x + 4sin⁡6x – 1 = 0$

Đặt $sin⁡ 6x = t$ với điều kiện $-1 ≤ t ≤ 1 (*)$,

ta được phương trình bậc hai theo $t$:

$-3t^2 + 4t – 1 = 0 (1)$

$Δ = 4^2 – 4.(-1).(-3) = 4$

Phương trình (1) có hai nghiệm là:

$\eqalign{
& {t_1} = {{ – 4 + \sqrt 4 } \over {2.( – 3)}} = {1 \over 3}(TM) \cr
& {t_2} = {{ – 4 – \sqrt 4 } \over {2.( – 3)}} = 1\,(TM) \cr} $

Ta có:

$sin⁡6x = {{ 1} \over 3}$

$⇔ 6x = arcsin {{ 1} \over 3} + k2π$ và $6x = π – arcsin {{ 1} \over 3} + k2π$

$⇔ x = {1 \over 6} arcsin {{ 1} \over 3} + {{k\pi } \over 3}$ và $x = {\pi \over 6} – {1 \over 6} arcsin {{ 1} \over 3} + {{k\pi } \over 3}, k ∈ Z$

$sin⁡ 6x = 1 ⇔ sin ⁡6x = \sin {{ \pi } \over 2}$

$⇔ 6x = {{ \pi } \over 2} + k2π, k ∈ Z$

$⇔ x = {{ \pi } \over 12} + {{k\pi } \over 3}, k ∈ Z$

5. Trả lời câu hỏi 5 trang 35 sgk Đại số và Giải tích 11

Dựa vào các công thức cộng đã học:

$sin(a + b) = sina cosb + sinb cosa$;

$sin(a – b) = sina cosb – sinb cosa$;

$cos(a + b) = cosa cosb – sina sinb$;

$cos(a – b) = cosa cosb + sina sinb$;

và kết quả cos ${\pi \over 4}$ = sin${\pi \over 4}$ = ${{\sqrt 2 } \over 2}$, hãy chứng minh rằng:

a) sinx + cosx = √2 cos(x – ${\pi \over 4}$);

b) sin x – cosx = √2 sin(x – ${\pi \over 4}$).

Trả lời:

Ta có:

a) sin⁡x + cos⁡x = √2.(${{\sqrt 2 } \over 2}$ sin⁡x + ${{\sqrt 2 } \over 2}$ cos⁡x )

= √2.(sin⁡ ${\pi \over 4}$ sin⁡x + cos⁡ ${\pi \over 4}$ cos⁡x )

= √2.cos⁡(x – ${\pi \over 4}$)

b) sin⁡x – cos⁡x = √2.(${{\sqrt 2 } \over 2}$ sin⁡x – ${{\sqrt 2 } \over 2}$ cos⁡x )

= √2.(cos⁡ ${\pi \over 4}$ sin⁡x + sin⁡ ${\pi \over 4}$ cos⁡x )

= √2.sin⁡(x – ${\pi \over 4}$)

6. Trả lời câu hỏi 6 trang 36 sgk Đại số và Giải tích 11

Giải phương trình $√3 sin3x – cos3x = √2.$

Trả lời:

$\eqalign{
& \sqrt 3 \sin 3x – \cos 3x = \sqrt 2 \cr
& \Leftrightarrow {{\sqrt 3 } \over 2}\sin 3x – {1 \over 2}\cos 3x = {{\sqrt 2 } \over 2} \cr
& \Leftrightarrow \cos {\pi \over 6}\sin 3x – \sin {\pi \over 6}\cos 3x = \sin {\pi \over 4} \cr
& \Leftrightarrow \sin (3x – {\pi \over 6}) = \sin {\pi \over 4} \cr
& \Leftrightarrow \left[ \matrix{
3x – {\pi \over 6} = {\pi \over 4} + k2\pi \hfill \cr
3x – {\pi \over 6} = \pi – {\pi \over 4} + k2\pi \hfill \cr} \right.;\,k \in Z \cr
& \Leftrightarrow \left[ \matrix{
3x = {5\pi \over 12} + k2\pi \hfill \cr
3x = {11\pi \over 12} + k2\pi \hfill \cr} \right.;k \in Z \cr
& \Leftrightarrow \left[ \matrix{
x = {5\pi \over 36} + k{{2\pi } \over 3} \hfill \cr
x = {11\pi \over 36} + k{{2\pi } \over 3} \hfill \cr} \right.;\,\,k \in Z \cr} $

Dưới đây là phần Hướng dẫn giải bài 1 2 3 4 5 6 trang 36 37 sgk Đại số và Giải tích 11. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập đại số và giải tích 11 kèm bài giải chi tiết bài 1 2 3 4 5 6 trang 36 37 sgk Đại số và Giải tích 11 của Bài §3. Một số phương trình lượng giác thường gặp trong Chương I. Hàm số lượng giác và phương trình lượng giác cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 6 trang 36 37 sgk Đại số và Giải tích 11

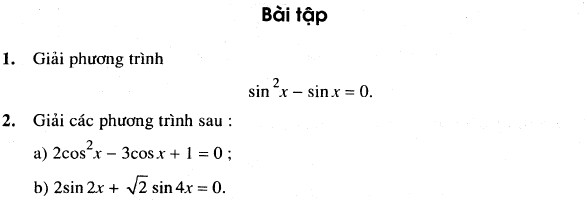
1. Giải bài 1 trang 36 sgk Đại số và Giải tích 11

Giải phương trình: $\small sin^2x – sinx = 0$

Bài giải:

Xét phương trình ${\sin ^2}x – \sin x = 0$

Đặt $t = \sin x, – 1 \le t \le 1.$ Phương trình trở thành:

${t^2} – t = 0 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 1\end{array} \right.$ (Thỏa mãn điều kiện)

$\Rightarrow \bigg \lbrack\begin{matrix} sinx=0\\ sinx=1 \end{matrix}$

$\Leftrightarrow \Bigg \lbrack\begin{matrix} x=k\pi \ \ \ \ \ \ \ \\ \\ x=\frac{\pi }{2}+k2 \pi \end{matrix}, (k\in Z)$

Vậy phương trình có nghiệm là: $\Bigg \lbrack\begin{matrix} x=k\pi \ \ \ \ \ \ \ \\ \\ x=\frac{\pi }{2}+k2 \pi \end{matrix}, (k\in \mathbb{Z})$.

2. Giải bài 2 trang 36 sgk Đại số và Giải tích 11

Giải các phương trình sau:

a) $\small 2cos^2x – 3cosx + 1 = 0$;

b) $\small 2sin2x + \sqrt{2}sin4x = 0$.

Bài giải:

a) $2cos^2x-3cosx+1=0$

Đặt $ t = cosx, t \in [-1 ; 1]$

Ta có phương trình $2t^2-3t+1=0\Leftrightarrow \Bigg \lbrack\begin{matrix} t=1\\ \\ t=\frac{1}{2} \end{matrix}$ (nhận)

$t=1\Leftrightarrow cosx=1\Leftrightarrow x=k2\pi, k\in \mathbb{Z}$

$t=\frac{1}{2}\Leftrightarrow cosx=\frac{1}{2} \Leftrightarrow cosx=cos\frac{\pi }{3},x=\pm \frac{\pi }{3}+k2 \pi, k\in \mathbb{Z}$

b) $2sin2x+\sqrt{2}sin4x=0$

$\Leftrightarrow 2sin2x+2\sqrt{2}sin2x.cos2x=0$

$\Leftrightarrow 2sin2x(1+\sqrt{2}cos2x)=0$

$\Leftrightarrow \Bigg \lbrack\begin{matrix} sin2x=0 \ \ \ \ \ \ \ \ \\ \\ \cos 2x = – \frac{1}{{\sqrt 2 }} \end{matrix}\Leftrightarrow \Bigg \lbrack\begin{matrix} sin2x=0 \ \ \ \ \ \ \ \ \\ \\ cos2x=cos\frac{3\pi }{4} \end{matrix}$

$\Leftrightarrow \Bigg \lbrack\begin{matrix} 2x=k\ pi, k\in \mathbb{Z}\\ \\ 2x=\pm \frac{3\pi }{4}+k2\pi,k\in \mathbb{Z} \end{matrix}\Leftrightarrow \Bigg \lbrack\begin{matrix} x=\frac{k\pi}{2},k\in \mathbb{Z} \ \ \ \ \ \ \ \\ \\ x= \pm \frac{3\pi}{8}+k\pi ,k\in \mathbb{Z} \end{matrix}$

Vậy phương trình có nghiệm là: $\Leftrightarrow \Bigg \lbrack\begin{matrix} x=\frac{k\pi}{2},k\in \mathbb{Z} \ \ \ \ \ \ \ \\ \\ x=\pm \frac{3\pi}{8}+k\pi ,k\in \mathbb{Z} \end{matrix}$

3. Giải bài 3 trang 37 sgk Đại số và Giải tích 11

Giải các phương trình sau:

a) $sin^2(\frac{x}{2}) – 2cos(\frac{x}{2}) + 2 = 0$;

b) $\small 8cos^2x + 2sinx – 7 = 0$;

c) $\small 2tan^2x + 3tanx + 1 = 0$;

d) $\small tanx -2cotx + 1 = 0$.

Bài giải:

a) $sin^2\frac{x}{2}-2cos\frac{x}{2}+2=0\Leftrightarrow 1-cos^2\frac{x}{2}- 2cos\frac{x}{2}+2=0$

$\Leftrightarrow cos^2\frac{x}{2}+2cos\frac{x}{2}-3=0$

Đặt $t=cos\frac{x}{2},-1\leq t\leq 1$, ta có phương trình:

$t^2+2t-3=0\Leftrightarrow \bigg \lbrack\begin{matrix} t=1\\ t=-3 \ \ (loại) \end{matrix}$

$t=1\Leftrightarrow cos\frac{x}{2}=1\Leftrightarrow \frac{x}{2}=k2\pi,k\in \mathbb{Z} \Leftrightarrow x=k 4 \pi, k\in \mathbb{Z}$

Vậy phương trình có nghiệm là: $x=k 4 \pi, k\in \mathbb{Z}$

b) $8cos^2x+2sinx-7=0\Leftrightarrow 8(1-sin^2x)+2sinx-7=0$

$\Leftrightarrow 8-8sin^2x+2sinx-7=0$

$\Leftrightarrow 8sin^2x-2sinx-1=0$

Đặt $t=sinx,-1\leq t\leq 1$, ta có phương trình:

$8t^2-2t-1=0\Leftrightarrow \Bigg \lbrack\begin{matrix} t=\frac{1}{2}\\ \\ t=-\frac{1}{4} \end{matrix} (nhận)$

$t=\frac{1}{2}\Leftrightarrow sinx=\frac{1}{2}\Leftrightarrow sinx=sin\frac{\pi }{6}\Leftrightarrow \Bigg \lbrack \begin{matrix} x=\frac{\pi }{6}+k2\pi \\ \\ x=\pi -\frac{\pi }{6}+k2\pi \end{matrix} k\in \mathbb{Z}$

$t=\frac{1}{4}\Leftrightarrow sinx=-\frac{1 }{4}\Leftrightarrow \Bigg \lbrack \begin{matrix} x=arcsin \left (-\frac{1 }{4} \right )+k2\pi , k\in \mathbb{Z}\\ \\ x=\pi -arcsin \left (-\frac{1 }{4} \right )+k2\pi , k\in \mathbb{Z} \end{matrix}$

Vậy phương trình có nghiệm là: $\Bigg \lbrack\begin{matrix} x=\frac{\pi }{6}+k2\pi\\ x=\frac{5\pi }{6}+k2\pi\\ x=arcsin \left ( -\frac{1}{4} \right )+k2\pi \\ x=\pi -arcsin \left ( -\frac{1}{4} \right )+k2\pi \end{matrix},k\in \mathbb{Z}$

c) $2tan^2x+3tanx+1=0$

Đặt t = tanx (điều kiện $x\neq \frac{\pi }{2}+k\pi , k\in \mathbb{Z}$)

Ta có phương trình: $2t^2+3t+1=0\Leftrightarrow \Bigg \lbrack\begin{matrix} t=1\\ \\ t=-\frac{1}{2} \end{matrix}$

$t=-1\Rightarrow tanx=-1\Rightarrow tanx=-tan\frac{\pi }{4}$

$\Rightarrow tanx=tan\left ( -\frac{\pi }{4} \right )\Rightarrow x=-\frac{\pi }{4} +k \pi$ (thoả mãn điều kiện)

$t=\frac{1}{2}\Rightarrow tanx=\frac{1}{2}\Rightarrow x=arctan \left ( \frac{1}{2} \right ) +k \pi$ (thoả mãn điều kiện)

Vậy phương trình có nghiệm là: $\Bigg \lbrack\begin{matrix} x=-\frac{\pi }{4} +k \pi \\ \\ x=arctan \left ( \frac{1}{2} \right )+k \pi \end{matrix}, (k\in \mathbb{Z})$

d) $tanx-2cotx+1=0$

Điều kiện $\left\{\begin{matrix} x\neq \frac{\pi }{2}+k \pi, k\in \mathbb{Z}\\ x\neq k \pi \end{matrix}\right.$ hay $x\neq k\frac{\pi }{2}, k\in \mathbb{Z}$

Đặt t = tanx, ta có phương trình:

$t-\frac{2}{t}+1=0\Rightarrow t^2+t-2=0\Rightarrow \bigg \lbrack\begin{matrix} t=1\\ t=-2 \end{matrix}$

$t=1\Rightarrow tanx=1$

$\Rightarrow tanx=tan\frac{\pi }{4}\Rightarrow x=\frac{\pi }{4}+k \pi, k\in \mathbb{Z}$ (thoả mãn điều kiện)

$t=-2\Rightarrow tanx=-2\Rightarrow x=arctan(-2)+k \pi, k\in \mathbb{Z}$ (thoả mãn điều kiện)

Vậy phương trình có nghiệm là: $\Bigg \lbrack\begin{matrix} x=\frac{\pi }{4}+k \pi \\ \\ x=arctan(-2)+k \pi \end{matrix}, k\in \mathbb{Z}$

4. Giải bài 4 trang 37 sgk Đại số và Giải tích 11

Giải các phương trình sau:

a) $\small 2sin^ 2x + sinxcosx – 3cos^2x = 0$

b) $\small 3sin^2x – 4sinxcosx + 5cos^2x = 2$

c) $\small 3sin^2x – sin2x + 2cos^2x = \frac{1}{2}$

d) $\small 2cos^2x -3\sqrt{3}sin2x -4sin^2x = -4$

Bài giải:

Phương pháp giải:

Xét phương trình: $a\sin {}^2x + b\sin x\cos x + c\cos {}^2x = d $

Xét $\cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}$ có là nghiệm của (1) hay không

Xét $\cos x \ne 0$, chia hai vế của (1) cho ${\cos ^2}x$ ta được:

$a{\tan ^2}x + b\tan x + c = d(1 + {\tan ^2}x)$

$ \Leftrightarrow \left( {a – d} \right){\tan ^2}x + b\tan x + c – d = 0$ $\left( {1′} \right)$

Đặt $t = \tan x$

Phương trình $\left( {1′} \right)$ trở thành: $(a – d){t^2} + bt + c – d = 0{\rm{ (2)}}$

Giải phương trình (2) theo t từ đó suy ra x theo $t = \tan x$.

Áp dụng:

a) Ta nhận thấy $cosx = 0$ không là nghiệm của phương trình. Chia hai vế cho cos²x ta được:

$\Rightarrow 2tan^2x+tanx-3=0$

$\Leftrightarrow \Bigg \lbrack \begin{matrix} tan x = 1\\ \\ tan x = -\frac{3}{2} \end{matrix}$

Vậy phương trình có nghiệm $\Bigg \lbrack\begin{matrix} x= \frac{\pi }{4}+k \pi \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ \\ x= arctan\left (-\frac{3}{2} \right )+k \pi \end{matrix} , k\in \mathbb{Z}$

b) Ta nhận thấy $cosx = 0$ không là nghiệm của phương trình:

$3sin^2x+4sinxcosx+5cos^2x=2$, nên chia hai vế phương trình cho cos²x ta được: $3tan^2x-4tanx+5=2(1+tan^2x)$

$\Leftrightarrow tan^2x-4tanx+3=0$

Đặt $t = tanx$

Ta có phương trình $t^2-4t+3=0 \Leftrightarrow \bigg \lbrack \begin{matrix} t=1\\ t=3 \end{matrix}$

$t=1\Rightarrow tanx=1\Rightarrow tanx=tan\frac{\pi }{4}\Rightarrow x=\frac{\pi }{4}+k \pi, k\in \mathbb{Z}$.

$t=3\Rightarrow tanx=3\Rightarrow x= arctan(3)+k \pi, (k\in \mathbb{Z})$

Vậy phương trình có nghiệm là: $\Bigg \lbrack\begin{matrix} x=\frac{\pi }{4}+k \pi \\ \\ x= arctan(3)+k \pi \end{matrix} , (k\in \mathbb{Z})$

c) $sin^2x+sin2x-2cos^2x=\frac{1}{2}\Leftrightarrow sin^2x+2sinxcosx-2cos^2x=\frac{1}{2}$ (3)

$cosx=0\Leftrightarrow x=\frac{\pi }{2}+k \pi, k\in \mathbb{Z}$ không là nghiệm của (3)

$cosx\neq 0$, chia hai vế của (3) cho $cos^2x$, ta được:

$\frac{sin^2x}{cos^2x}+\frac{2sinx}{cosx}-2=\frac{1}{2cos^2x}\Rightarrow tan^2x+2tanx-2=\frac{1}{2}(1+tan^2x)$

$\Rightarrow 2tan^2x+4tanx-4=1+tan^2x$

$\Rightarrow tan^2x +4tanx-5=0$

Đặt $t = tanx$, ta có phương trình:

$t^2+4t-5=0\Leftrightarrow \bigg \lbrack\begin{matrix} t=1\\ t=-5 \end{matrix}$

$t=1\Rightarrow tanx=1\Rightarrow x=\frac{\pi }{4}+k \pi, k\in \mathbb{Z}$

$t=-5 \Rightarrow tanx=-5\Rightarrow x=arctan(-5)+k\pi, k\in \mathbb{Z}$

Vậy phương trình có nghiệm $\bigg \lbrack\begin{matrix} x=\frac{\pi }{4}+k \pi \\ \\ x=arctan(-5)+k\pi \end{matrix}, k\in \mathbb{Z}$

d) $2cos^2x – 3\sqrt{3}sin2x – 4sin^2x = -4$

$\Leftrightarrow 2cos^2x – 6\sqrt{3}sinxcosx -4(1-cos^2x)+4= 0$

$\Leftrightarrow 2cos^2x – 6\sqrt{3}sinxcosx – 4+4cos^2x+4= 0$

$\Leftrightarrow 6cos^2x-6\sqrt{3}sinxcosx=2$

$\Leftrightarrow 6cosx(cosx – \sqrt{3}sinx) = 0$

$\Bigg \lbrack\begin{matrix} cosx=0\\ \\ cosx-\sqrt{3}sinx=0 \end{matrix}\Leftrightarrow \Bigg \lbrack\begin{matrix} x=\frac{\pi }{2}+k\pi,k\in \mathbb{Z}\\ \\ cosx=\sqrt{3}sinx \end{matrix}$

$\Leftrightarrow \bigg \lbrack\begin{matrix} x=\frac{\pi }{2}+k\pi, k\in \mathbb{Z}\\ \\ tanx=\frac{1}{\sqrt{3}} \end{matrix}\Leftrightarrow \Bigg \lbrack\begin{matrix} x=\frac{\pi }{2}+k\pi\\ \\ x=\frac{\pi }{6}+k\pi \end{matrix}, k\in \mathbb{Z}$

Vậy phương trình có nghiệm là $\Bigg \lbrack\begin{matrix} x=\frac{\pi }{2}+k\pi\\ \\ x=\frac{\pi }{6}+k\pi \end{matrix}, k\in \mathbb{Z}$

5. Giải bài 5 trang 37 sgk Đại số và Giải tích 11

Giải các phương trình sau:

a) $\small cosx – \sqrt{3}sinx = \sqrt{2}$

b) $\small 3sin3x – 4cos3x = 5$

c) $\small 2sin2x + 2cos2x -\sqrt{2} = 0$

d) $\small 5cos2x + 12sin2x – 13 = 0$

Bài giải:

Phương pháp giải:

Xét phương trình: $a\sin x + b\cos x = c{\rm{ (1)}}$

Điều kiện có nghiệm: ${a^2} + {b^2} \ge {c^2}$

Chia hai vế của (1) cho $\sqrt {{a^2} + {b^2}} $, ta được:

$\left( 1 \right) \Leftrightarrow \frac{a}{{\sqrt {{a^2} + {b^2}} }}\sin x + \frac{b}{{\sqrt {{a^2} + {b^2}} }}\cos x = \frac{c}{{\sqrt {{a^2} + {b^2}} }}$

Phương trình trở thành:

$\sin x\sin \varphi + \cos x\cos \varphi = \frac{c}{{\sqrt {{a^2} + {b^2}} }} \Leftrightarrow \cos \left( {x – \varphi } \right) = \frac{c}{{\sqrt {{a^2} + {b^2}} }}$

Đặt $\cos \alpha = \frac{c}{{\sqrt {{a^2} + {b^2}} }}$ ta được phương trình lượng giác cơ bản.

Hoàn toàn tương tự ta cũng có thể đặt $\left\{ \begin{array}{l}\cos \varphi = \frac{a}{{\sqrt {{a^2} + {b^2}} }}\\\sin \varphi = \frac{b}{{\sqrt {{a^2} + {b^2}} }}\end{array} \right.$

Áp dụng:

a) $\cos x – \sqrt 3 \sin x = \sqrt 2 $

$\begin{array}{l} \Leftrightarrow \frac{1}{2}\cos x – \frac{{\sqrt 3 }}{2}{\mathop{\rm sinx}\nolimits} = \frac{1}{{\sqrt 2 }}\\ \Leftrightarrow \sin \frac{\pi }{6}.\cos x – \cos \frac{\pi }{6}.\sin x = \frac{1}{{\sqrt 2 }}\\ \Leftrightarrow \sin \left( {\frac{\pi }{6} – x} \right) = \frac{1}{{\sqrt 2 }} \Leftrightarrow \sin \left( {\frac{\pi }{6} – x} \right) = \sin \frac{\pi }{4}\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{6} – x = \frac{\pi }{4} + k2\pi \\\frac{\pi }{6} – x = \frac{{3\pi }}{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = – \frac{\pi }{{12}} + k2\pi \\x = – \frac{{7\pi }}{{12}} + k2\pi \end{array} \right.,k \in \mathbb{Z}.\end{array}$

b) $3\sin 3x – 4\cos 3x = 5 \Leftrightarrow \frac{3}{5}\sin 3x – \frac{4}{5}\cos 3x = 1.$

Đặt $\cos \alpha = \frac{3}{5},\,\sin \alpha = \frac{4}{5},$ suy ra:

$\sin (3x – \alpha ) = 1 \Leftrightarrow 3x – \alpha = \frac{\pi }{2} + k2\pi \Leftrightarrow x = \frac{\pi }{6} + \frac{\alpha }{3} + k\frac{{2\pi }}{3},k \in \mathbb{Z}.$

c) Ta có:

$\begin{array}{l}2\sin x + 2{\mathop{\rm cosx}\nolimits} – \sqrt 2 = 0\\ \Leftrightarrow \sin x + \cos x = \frac{1}{{\sqrt 2 }}\\ \Leftrightarrow \sqrt 2 \sin \left( {x + \frac{\pi }{4}} \right) = \frac{1}{{\sqrt 2 }}\\ \Leftrightarrow \sin \left( {x + \frac{\pi }{4}} \right) = \frac{1}{2}\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{4} = \frac{\pi }{6} + k2\pi \\x + \frac{\pi }{4} = \frac{{5\pi }}{6} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = – \frac{\pi }{{12}} + k2\pi \\x = \frac{{7\pi }}{{12}} + k2\pi \end{array} \right.,k \in \mathbb{Z}.\end{array}$

d) Ta có:

$\begin{array}{l}5\cos 2x + 12\sin 2x – 13 = 0\\ \Leftrightarrow 12\sin 2x + 5\cos 2x = 13\\ \Leftrightarrow \frac{{12}}{{13}}\sin 2x + \frac{5}{{13}}\cos 2x = 1\end{array}$

$ \Leftrightarrow \sin (2x + \alpha ) = 1$ $\left( {\sin \alpha = \frac{5}{{13}};\,\cos \alpha = \frac{{12}}{{13}}} \right)$

$\begin{array}{l} \Leftrightarrow 2x + \alpha = \frac{\pi }{2} + k2\pi \\ \Leftrightarrow x = \frac{\pi }{4} – \frac{\alpha }{2} + k\pi ,k \in \mathbb{Z}.\end{array}$

6. Giải bài 6 trang 37 sgk Đại số và Giải tích 11

Giải phương trình:

a) $\small tan(2x + 1) tan(3x – 1) = 1$

b) $\small tanx + tan(x + \frac{\pi }{4}) = 1$

Bài giải:

Phương pháp giải:

Câu a: Sử dụng công thức $\tan x = \frac{{\sin x}}{{\cos x}}$ và $\cos (a + b) = \cos a.\cos b – \sin a.\sin b$ để biến đổi phương trình.

Câu b: Sử dụng công thức $\tan x = \frac{{\sin x}}{{\cos x}}$; $\sin (a + b) = \sin a.\cos b + {\mathop{\rm cosa}\nolimits} .\sin b$ và $\cos a.\cos b = \frac{1}{2}\left[ {\cos (a + b) + \cos (a – b)} \right]$ để biến đổi phương trình.

Áp dụng:

a) Với điều kiện $\left\{\begin{matrix} 2x+1\neq \frac{\pi }{2}+k \pi\\ \\ 3x-1\neq \frac{\pi }{2}+k \pi \end{matrix}\right. , k\in \mathbb{Z}$ hay $\left\{\begin{matrix} x\neq \frac{\pi }{4}-\frac{1}{2}+\frac{k \pi}{2}\\ \\ x\neq \frac{\pi }{6}+\frac{1}{2}+\frac{k \pi}{3} \end{matrix}\right. , k\in \mathbb{Z}$

$\Leftrightarrow tan(2x + 1) tan(3x – 1) = 1$

(1) $\Leftrightarrow \frac{sin(2x+1)sin(3x-1)}{cos(2x+1)cos(2x-1)}=1$

$ \Rightarrow \cos(2x+1) \cos(3x-1)-\sin(2x+1) \sin(3x-1) =0$

$\Leftrightarrow cos(2x+1+3x-1)\Leftrightarrow cos5x=0$

$\Leftrightarrow 5x=\frac{\pi }{2}+k\pi,k\in \mathbb{Z}$

$\Leftrightarrow x=\frac{\pi }{10}+\frac{k \pi}{5},k\in \mathbb{Z}$ (thoả mãn điều kiện)

Vậy phương trình có nghiệm $x=\frac{\pi }{10}+\frac{k \pi}{5},k\in \mathbb{Z}.$

b) Điều kiện $\left\{\begin{matrix} cosx\neq 0\\ cos(x+\frac{\pi }{4})\neq 0 \end{matrix}\right.$

Khi đó $tanx+tan\left ( x+\frac{\pi }{4} \right )=1$

$\Leftrightarrow sinx.cos\left ( x+\frac{\pi }{4} \right )+cosx.sin\left ( x+\frac{\pi }{4} \right )= cosx.cos\left ( x+\frac{\pi }{4} \right )$

$\Leftrightarrow sin\left ( 2x+\frac{\pi }{4} \right )=\frac{1}{2} \left [ cos\left ( 2x+\frac{\pi }{4} \right ) +cos \left ( – \frac{\pi }{4}\right )\right ]$

$\Leftrightarrow 2sin\left ( 2x+\frac{\pi }{4} \right )-cos\left (2 x+\frac{\pi }{4} \right )= \frac{\sqrt{2}}{2}$

$\Leftrightarrow \frac{2}{\sqrt{5}}sin\left ( 2x+\frac{\pi }{4} \right ) -\frac{1}{\sqrt{5}}cos \left (2x+\frac{\pi }{4} \right )=\frac{\sqrt{2}}{10}$

$\Leftrightarrow sin\left (2x+\frac{\pi }{4} -\alpha \right )=\frac{\sqrt{2}}{10}$

$\Leftrightarrow \Bigg \lbrack \begin{matrix} 2x+\frac{\pi }{4}-\alpha = arcsin \frac{\sqrt{2}}{10} + k2 \pi\\ \\ 2x+\frac{\pi }{4}-\alpha = \pi – arcsin \frac{\sqrt{2}}{10} + k2 \pi \end{matrix}$

$\Leftrightarrow \Bigg \lbrack \begin{matrix} x= \frac{\alpha }{2}-\frac{\pi }{8}+ \frac{1}{2}arcsin \frac{\sqrt{2}}{10} + k\pi\\ \\ x = \frac{\alpha }{2}+\frac{3\pi }{8}- \frac{1}{2} arcsin \frac{\sqrt{2}}{10} + k\pi \end{matrix}, k\notin \mathbb{Z}$

Bài trước:

Giải bài 1 2 3 4 5 6 7 trang 28 29 sgk Đại số và Giải tích 11

Bài tiếp theo:

Ôn tập chương I: Giải bài 1 2 3 4 5 6 7 8 9 10 trang 40 41 sgk Đại số và Giải tích 11

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 11 với giải bài 1 2 3 4 5 6 trang 36 37 sgk Đại số và Giải tích 11!

“Bài tập nào khó đã có giaibaisgk.com“