Hướng dẫn Giải bài 1 2 3 4 5 6 trang 57 58 sgk Đại số và Giải tích 11

Nội Dung

Hướng dẫn giải Bài §3. Nhị thức Niu – Tơn, Chương II. Tổ hợp – Xác suất, sách giáo khoa Đại số và Giải tích 11. Nội dung bài giải bài 1 2 3 4 5 6 trang 57 58 sgk Đại số và Giải tích 11 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập đại số và giải tích có trong SGK để giúp các em học sinh học tốt môn toán lớp 11.

Lý thuyết

I. Công thức nhị thức Niu – Tơn

Với $a, b$ là những số thực tùy ý và với mọi số tự nhiên $n ≥ 1$, ta có:

${(a + b)^n} = C_n^0{a^n} + C_n^1{a^{n – 1}}b + … +$

$C_n^{n – 1}a{b^{n – 1}} + C_n^n{b^n}(1)$

Quy ước:

Với $a$ là số thực khác $0$ và $n$ là số tự nhiên khác $0$, ta quy ước:

$a^0 = 1$; $a^{-n}= {1 \over {{a^n}}}$.

Chú ý:

Với các điều kiện và quy ước ở trên, đồng thời thêm điều kiện $a$ và $b$ đều khác $0$, có thể viết công thức (1) ở dạng sau đây:

${\left( {a + b} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n – k}}{b^k} = \sum\limits_{k = 0}^n {{a^k}{b^{n – k}}} } $

II. Tam giác Pa-Xcan (Pascal)

Tam giác Pascal là tam giác số ghi trong bảng:

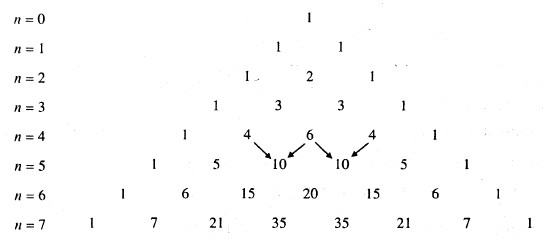
Cấu tạo của tam giác Pascal:

– Các số ở cột ) và ở “đường chéo” đều bằng $1$.

– Xét hai số ở cột $k$ và cột $k + 1$, đồng thời cùng thuộc dòng $n$, ($k ≥ 0; n ≥1$), ta có: tổng của hai số này bằng số đứng ở giao của cột $k + 1$ và dòng $n + 1$.

Tính chất của tam giác Pascal:

Từ cấu tạo của tam giác Pascal, có thể chứng minh được rằng:

a) Giao của dòng $n$ và cột $k$ là $C_n^k$

b) Các số của tam giác Pascal thỏa mãn công thức Pascal:

$C_n^k + C_n^{k + 1} = C_{n + 1}^{k + 1}$

c) Các số ở dòng $n$ là các hệ số trong khai triển của nhị thức ${(a + b)}^n$ (theo công thức nhị thức Niu – Tơn), với $a, b$ là hai số thực tùy ý. Chẳng hạn, các số ở dòng $4$ là các hệ số trong khai triển của $(a + b)^4$ (theo công thức nhị thức Niu – Tơn) dưới đây:

${\left( {a{\rm{ }} + {\rm{ }}b} \right)^4} = {\rm{ }}{a^4} + {\rm{ }}4{a^3}b{\rm{ }} + {\rm{ }}6{a^2}{b^{2}} + {\rm{ }}4a{b^3}{\rm{ }} + {\rm{ }}{b^4}$.

III. Bài toán

Xác định hệ số của số hạng chứa ${x^m}$ trong khai triển:

${\left( {a{x^p} + b{x^q}} \right)^n}$ với $x > 0$ ($p,q$ là các hằng số khác nhau).

Phương pháp giải:

Ta có:

${\left( {a{x^p} + b{x^q}} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{{\left( {a{x^p}} \right)}^{n – k}}{{\left( {b{x^q}} \right)}^k}} = \sum\limits_{k = 0}^n {C_n^k{a^{n – k}}{b^k}{x^{np – pk + qk}}} $

Số hạng chứa ${x^m}$ ứng với giá trị $k$ thỏa: $np – pk + qk = m$.

Từ đó tìm $k = \frac{{m – np}}{{p – q}}$

Vậy hệ số của số hạng chứa ${x^m}$ là: $C_n^k{a^{n – k}}.{b^k}$ với giá trị $k$ đã tìm được ở trên.

Nếu $k$ không nguyên hoặc $k > n$ thì trong khai triển không chứa ${x^m}$, hệ số phải tìm bằng 0.

Chú ý: Xác định hệ số của số hạng chứa ${x^m}$ trong khai triển

$P\left( x \right) = {\left( {a + b{x^p} + c{x^q}} \right)^n}$ được viết dưới dạng ${a_0} + {a_1}x + … + {a_{2n}}{x^{2n}}$.

Ta làm như sau:

Viết $P\left( x \right) = {\left( {a + b{x^p} + c{x^q}} \right)^n} = \sum\limits_{k = 0}^n {C_n^k{a^{n – k}}{{\left( {b{x^p} + c{x^q}} \right)}^k}} $;

Viết số hạng tổng quát khi khai triển các số hạng dạng ${\left( {b{x^p} + c{x^q}} \right)^k}$ thành một đa thức theo luỹ thừa của x.

Từ số hạng tổng quát của hai khai triển trên ta tính được hệ số của ${x^m}$.

Chú ý: Để xác định hệ số lớn nhất trong khai triển nhị thức Niutơn

Ta làm như sau:

Tính hệ số ${a_k}$ theo $k$ và $n$;

Giải bất phương trình ${a_{k – 1}} \le {a_k}$ với ẩn số $k$;

Hệ số lớn nhất phải tìm ứng với số tự nhiên k lớn nhất thoả mãn bất phương trình trên.

Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong phần hoạt động của học sinh sgk Đại số và Giải tích 11.

Câu hỏi

1. Trả lời câu hỏi 1 trang 55 sgk Đại số và Giải tích 11

Khai triển biểu thức (a + b)⁴ thành tổng các đơn thức.

Trả lời:

Ta có:

(a + b)⁴ = (a + b)³(a + b)

= (a³ + 3a²b + 3ab² + b³ )(a + b)

= a⁴ + 3a³b + 3a²b² + ab³ + a³b + 3a²b² + 3ab³ + b⁴

= a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

2. Trả lời câu hỏi 2 trang 57 sgk Đại số và Giải tích 11

Dùng tam giác Pa-xcan, chứng tỏ rằng:

a) $1 + 2 + 3 + 4 $= C²₅;

b) $1 + 2 + … + 7 $= C²₈.

Trả lời:

a) Dựa vào tam giác Pa-xcan:

C¹₄ = 4; C²₄ = 6; C²₅ = C¹₄ + C²₄ $= 4 + 6 = 10$

Mà: $1 + 2 + 3 + 4 = 10$

⇒ $1 + 2 + 3 + 4 $= C²₅

b) Dựa vào tam giác Pa-xcan:

C¹₇ = 7; C²₇ = 21 ;C²₈ = C¹₇ + C²₇ $= 7 + 21 = 28$

$1 + 2 +⋯+ 7 =$ ((1 + 7).7)/2 $= 28$

$⇒ 1 + 2 +⋯+ 7 $= C²₈

Dưới đây là phần Hướng dẫn giải bài 1 2 3 4 5 6 trang 57 58 sgk Đại số và Giải tích 11. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập đại số và giải tích 11 kèm bài giải chi tiết bài 1 2 3 4 5 6 trang 57 58 sgk Đại số và Giải tích 11 của Bài §3. Nhị thức Niu – Tơn trong Chương II. Tổ hợp – Xác suất cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 6 trang 57 58 sgk Đại số và Giải tích 11

1. Giải bài 1 trang 57 sgk Đại số và Giải tích 11

Viết khai triển theo công thức nhị thức Niu – Tơn:

a) $(a + 2b)^5$;

b) $\small (a – \sqrt{2})^6$;

c) $\small (x – \frac{1}{x})^{13}$.

Bài giải:

a) Ta có:

$(a + 2b)^5= C_{5}^{0}a^5+C_{5}^{1}a^4(2b)+C_{5}^{2}a^3(2b)^2$

$+ C_{5}^{3}a^2(2b)^3+C_{5}^{4}a(2b)^4+C_{5}^{5}(2b)^5$

$= a^5 + 10a^4b + 40a^3b^2 + 80a^2b^3 + 80ab^4 + 32b^5$

b) Theo dòng 6 của tam giác Pascal, ta có:

$(a – \sqrt{2})^6 = [a + (\sqrt{2})]^6$

$=a^6 + 6a^5 (\sqrt{2}) + 15a^4 (\sqrt{2})^2 + 20a^3 (\sqrt{2})^3$

$+ 15a^2 (\sqrt{2})^4 + 6a(\sqrt{2})^5 + (-\sqrt{2})^6.$

$= a^6 – 6\sqrt{2}a^5 + 30a^4 – 40\sqrt{2}a^3 + 60a^2 – 20\sqrt{2}a + 8.$

c) Theo công thức nhị thức Niu – Tơn, ta có:

$\left ( x-\frac{1}{x} \right )^{13}=C_{13}^{0}x^{13}-C_{13}^{1}x^{12}\frac{1}{x}+ C_{13}^{2}x^{11}\frac{1}{x^2}-C_{13}^{3}x^{10}\frac{1}{x^3}$

$+C_{13}^{4}x^{9}\frac{1}{x^4}-C_{13}^{5}x^{8}\frac{1}{x^5}+ C_{13}^{6}x^{7}\frac{1}{x^6} -C_{13}^{7}x^{6}\frac{1}{x^7}$

$+ C_{13}^{8}x^{5}\frac{1}{x^8}-C_{13}^{9}x^{4}\frac{1}{x^9}+ C_{13}^{10}x^{3}\frac{1}{x^{10}}-C_{13}^{11}x^{2}\frac{1}{x^{11}}$

$+C_{13}^{12}x\frac{1}{x^{12}}-C_{13}^{13}\frac{1}{x^{13}}$

$=x^{13}-13x^{11}+78x^{9}-286x^{7}+715x^{5}-1287x^{3}+1716x$

$-\frac{1716}{x}+\frac{1287}{x^3}-\frac{715}{x^5}+\frac{286}{x^7}- \frac{78}{x^9}+\frac{13}{x^{11}}-\frac{1}{x^{13}}$

2. Giải bài 2 trang 58 sgk Đại số và Giải tích 11

Tìm hệ số của x³ trong khai triển của biểu thức: $\small (x +\frac{2}{x^2} )^6$.

Bài giải:

Số hạng tổng quát của khai triển là: $C_{6}^{k}.x^{6-k}.\left ( \frac{2}{x^2} \right )^k$

Ta có: $C_{6}^{k}.x^{6-k}.\left ( \frac{2}{x^2} \right )^k=2^k.C_{6}^{k}.x^{6-k}.x^{2k}= 2^k.C_{6}^{k}.x^{6-3k}$

Số hạng chứa $x^3$ trong khai triển sẽ là $2^k.C_{6}^{k}.x^{6-3k}$ với $6-3k=3$.

Từ (1) ta có $3k=6-3\Leftrightarrow 3k=3\Leftrightarrow k=1$

Ta có: $2^1C_{6}^{1}=2.\frac{6!}{1!(6-1)!}=2.6=12$

Vậy hệ số của $x^3$ trong khai triển bằng 12.

3. Giải bài 3 trang 58 sgk Đại số và Giải tích 11

Biết hệ số của x²trong khai triển của $\small (1 – 3x)^n$ là $90$. Tìm $n$.

Bài giải:

Ta có $(1-3x)^n=C_{n}^{0}-C_{n}^{1}3x+C_{n}^{2}(3x)^2-C_{n}^{3}(3x)^3+…+ C_{n}^{n}(-3x)^n.$

Từ đây, ta có hệ số của $x^2$ là $9C_{n}^{2}$. Do đó, ta có:

$9C_{n}^{2}=90\Leftrightarrow C^2_n=10\Leftrightarrow \frac{n!}{(n-2)!.2!}=10\Leftrightarrow n(n-1)=20$

$\Leftrightarrow n^2 – n – 10 = 0\Leftrightarrow n = 5 (vi \ n\in \mathbb{N})$

4. Giải bài 4 trang 58 sgk Đại số và Giải tích 11

Tìm số hạng không chứa x trong khai triển của $\small (x^3 +\frac{1}{x} )^8$.

Bài giải:

Số hạng tổng quát của khai triển là: $C_{8}^{k}(x^3)^{8-k}.\left ( \frac{1}{x} \right )^k= C_{8}^{k}x^{24-3k}x^{-k}=C_{8}^{k}.x^{24-4k}$

Số hạng không chứa $x$ trong khai triển ứng với giá trị của $k$ là:

$24-4k=0\Leftrightarrow k=6$

Ta có: $C_{8}^{6}=\frac{8!}{6!(8-6)!}=28$

Vậy số hạng không chứa x trong khai triển là $28$.

5. Giải bài 5 trang 58 sgk Đại số và Giải tích 11

Từ khai triển biểu thức $\small (3x – 4)^ {17 }$ thành đa thức, hãy tính tổng các hệ số của đa thức nhận được:

Bài giải:

Đặt $f(x)=(3x-4)^{17}=a_{17}x^{17}+a_{16}x^{16}+…+a_{1}x+a_0$

Ta cần tính: $a_0+a_1+a_2+…+a_{17}$

Dễ thấy $f(1)=(3-4)^{17}=a_+a_1+…+a_{17}$

$\Leftrightarrow a_0+a_1+a_2+…+a_{17}=-1$

6. Giải bài 6 trang 58 sgk Đại số và Giải tích 11

Chứng minh rằng:

a) $\small 11^{10} – 1$ chia hết cho $100$;

b) $\small 101^{100} – 1$ chia hết cho $10 000$;

c) $\small \sqrt{10}[(1+\sqrt{10})^{100}-(1-\sqrt{10})^{100}]$ là một số nguyên.

Bài giải:

a) Ta có:

$11^{10}- 1 = (1 + 10)^{10} =C_{10}^{0}.10^{10}+C_{10}^{1}.10^9+…$$+ C_{10}^{8}.10^2+C_{10}^{9}.10+C_{10}^{10}$

$=100(C_{10}^{0}.10^8+C_{10}^{1}.10^7+…+ C_{10}^{8}+1)+1$

Tổng sau cùng chia hết cho 100 suy ra 11¹⁰ – 1 chia hết cho 100.

b) Ta có:

$101^{100}=(100+1)^{100}=C_{100}^{0}.100^{100}$

$+C_{100}^{1}.100^{99}+…+ C_{100}^{99}.100+C_{100}^{100}$

$=100^2\left [ C_{100}^{0}.100^{98}+C_{100}^{1}.100^{97}+…+1 \right ]$

Vậy $101^{100}=10000\left [ C_{100}^{0}.100^{98}+C_{100}^{1}.100^{97}+…+1 \right ]$ chia hết cho 10 000.

c) Ta có:

$(1+\sqrt{10})^{100}=C_{100}^{0}+C_{100}^{1}\sqrt{10}+C_{100}^{2}\sqrt{10^2}+…+$$C_{100}^{99}\sqrt{10^{99}}+C_{100}^{100}$

$(1-\sqrt{10})^{100}=C_{100}^{0}+C_{100}^{1}\sqrt{10}+C_{100}^{2}\sqrt{10^2}+…-$$C_{100}^{99}\sqrt{10^{99}}+C_{100}^{100}$

Do đó: $(1+\sqrt{10})^{100}-(1-\sqrt{10})^{100}=2 \left ( C_{100}^{0}+C_{100}^{1}\sqrt{10}+C_{100}^{2}\sqrt{10^2}+…+ C_{100}^{99}\sqrt{10^{99}}\right )$

Vậy nên: $\sqrt{40}\left [ (1+\sqrt{10})^{100}-(1-\sqrt{10})^{100} \right ].$

Bài trước:

Giải bài 1 2 3 4 5 6 7 trang 54 55 sgk Đại số và Giải tích 11

Bài tiếp theo:

Giải bài 1 2 3 4 5 6 7 trang 63 64 sgk Đại số và Giải tích 11

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 11 với giải bài 1 2 3 4 5 6 trang 57 58 sgk Đại số và Giải tích 11!

“Bài tập nào khó đã có giaibaisgk.com“