Nội Dung
Hướng dẫn giải Bài §3. Ứng dụng của tích phân trong hình học, Chương 3. Nguyên hàm – Tích phân và ứng dụng, sách giáo khoa Giải tích 12. Nội dung bài giải bài 1 2 3 4 5 trang 123 sgk Giải tích 12 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập giải tích có trong SGK để giúp các em học sinh học tốt môn toán lớp 12.
Lý thuyết
1. Tính diện tích hình phẳng
Nếu hàm số \(y=f(x)\) liên tục trên \([a;b]\) thì diện tích S của hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a,x=b\) là \(S = \int\limits_a^b {\left| {f(x)} \right|dx} .\)

Diện tích hình phẳng giới hạn bởi các đồ thị hàm số \(y = f(x)\), \(y = g(x)\) và hai đường thẳng \(x=a,x=b\) là: \(S = \int\limits_a^b {\left| {f(x) – g(x)} \right|dx}\)

2. Tính thể tích
a) Thể tích của vật thể
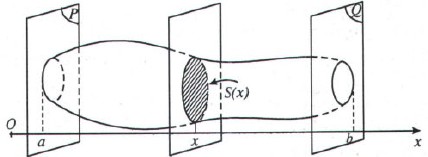
Thể tích vật thể B giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại các điểm \(a,b\) là \(V = \int\limits_a^b {S(x)dx}.\) Trong đó S(x) là diện tích thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là \(x \in \left[ {a;\,b} \right]\) và S(x) là một hàm liên tục.
b) Thể tích của khối tròn xoay
Hàm số \(y=f(x)\) liên tục và không âm trên \([a,b].\) Hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), trục hoành và hai đường thẳng \(x=a,x=b\) quay quanh trục hoành tạo nên một khối tròn xoay. Thể tích V được tính bởi công thức \(V = \pi \int\limits_a^b {{f^2}(x)dx} .\)

Cho hai hàm số \(y=f(x)\), \(y=g(x)\) thỏa \(0\leq g(x)\leq f(x)\), liên tục và không âm trên \([a,b].\) Hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\), \(y=g(x)\) và hai đường thẳng \(x=a,x=b\) quay quanh trục hoành tạo nên một khối tròn xoay. Thể tích V được tính bởi công thức \(V = \pi \int\limits_a^b {\left[ {{f^2}(x) – {g^2}(x)} \right]dx}.\)
Cho hai hàm số hình phẳng giới hạn bởi đồ thị hàm số \(y=f(x)\) và \(y=g(x)\) quay quanh trục hoành hoành tạo nên một khối tròn xoay. Để tính được thể tích khối tròn xoay ta thực hiện các bước:
Giải phương trình \(f(x) = g(x) \Leftrightarrow \left[ \begin{array}{l} x = a\\ x = b \end{array} \right.\) (Thường dạng bài này đề bài cho phương trình hoành độ giao điểm có hai nghiệm phân biệt).
Giải sử \(0\leq g(x)\leq f(x)\) với mọi x thuộc \([a,b].\) Khi đó: \(V = \pi \int\limits_a^b {\left[ {{f^2}(x) – {g^2}(x)} \right]dx}.\)
Hình phẳng giới hạn bởi đồ thị hàm số \(x = g(y)\), trục tung và hai đường thẳng \(y = c,\,y = d\) quay quanh trục tung tạo nên một khối tròn xoay. Thể tích V được tính bởi công thức \(V = \pi \int\limits_c^d {{g^2}(y)dy}.\)
Câu hỏi
1. Trả lời câu hỏi 1 trang 116 sgk Giải tích 12
Tính diện tích hình thang vuông được giới hạn các đường thẳng $y = -2x – 1, y = 0, x = 1$ và $x = 5$.
So sánh với hình thang vuông trong ![]() 1 của §2.
1 của §2.
Trả lời:
Ta có diện tích hình thang cần tính:
![]()
⇒ Diện tích hai hình thang vuông bằng nhau.
2. Trả lời câu hỏi 2 trang 119 sgk Giải tích 12
Hãy nhắc lại công thức tính thể tích khối lăng trụ có diện tích đáy bằng $B$ và chiều cao bằng $h$.
Trả lời:
Công thức tính thể tích lăng trụ có diện tích đáy là $B$ và chiều cao là $h$ là: $V = B.h$.
3. Trả lời câu hỏi 3 trang 121 sgk Giải tích 12
Nhắc lại khái niệm mặt tròn xoay và khối tròn xoay trong hình học.
Trả lời:
– Khái niệm mặt tròn xoay: Trong không gian cho mặt phẳng $(P)$ chứa đường thẳng $Δ$ và chứ đường $L$. Khi quay mặt $(P)$ xung quanh $Δ$ một góc $360^0$ thì đường $L$ tạo nên một mặt tròn xoay. Mặt tròn xoay đó nhận $Δ$ làm trục, đường $L$ được gọi là đường sinh.
– Khái niệm khối tròn xoay: Khối tròn xoay là khối hình học được tạo thành khi quay một hình phẳng quanh một đường thẳng cố định (trục quay) của hình.
Dưới đây là Hướng dẫn giải bài 1 2 3 4 5 trang 123 sgk Giải tích 12. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập giải tích 12 kèm bài giải chi tiết bài 1 2 3 4 5 trang 123 sgk Giải tích 12 của Bài §3. Ứng dụng của tích phân trong hình học của hàm số trong Chương 3. Nguyên hàm – Tích phân và ứng dụng cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 1 trang 123 sgk Giải tích 12
Tính diện tích hình phẳng giới hạn bởi các đường:
a) \(y = x^2, y = x + 2\);
b) \(y = |lnx|, y = 1\);
c) \(y = (x – 6)^2, y = 6x- x^2\)
Bài giải:
a) Xét phương trình:
\(x^2=x+2\Leftrightarrow x^2-x-2=0\Leftrightarrow x=-1;x=2\)
⇒ Diện tích hình phẳng giới hạn bởi đường cong \(y=x^2\) và đường thẳng \(y=x+2\) là:
\(S=\int_{1}^{2} \left | x^2-(x+2) \right |dx= \int_{1}^{2}\left | x^2-x-2 \right |dx\)
Vì \(x^2-x-2\leq 0\) khi \(-1\leq x\leq 2\)
nên \(S=-\int_{1}^{2}(x^2-x-2)dx= \left ( -\frac{x^3}{3} +\frac{x^2}{2} +2x \right ) \Bigg|^2_1\)
\(=\left ( -\frac{8}{3}+2+4 \right )-\left ( \frac{1}{3}+\frac{1}{2}-2 \right )= \frac{9}{2}\)
Vậy \(S=\frac{9}{2}\) (đvdt)
b) Xét phương trình: \(\left | lnx \right | =1\Leftrightarrow x=e;x=\frac{1}{e}\)
Do đó diện tích cần tìm là: \(S=\int_{1}^{e} \left |\left | lnx \right |-1 \right |dx\)
Ta có: \(\left | lnx \right | = \left\{\begin{matrix} ln x \ neu \ x\geq 1\\ -lnx \ neu \ 0< x\leq 1 \end{matrix}\right.\)
Do đó:
\(S=\int^{e}_{\frac{1}{e}}\left |\left | lnx \right |-1 \right |dx= \int^{e}_{\frac{1}{e}} \left | lnx-1 \right |dx+\int^{e}_{\frac{1}{e}} \left | -lnx-1 \right |dx\)
\(=\int^{e}_{\frac{1}{e}}(1-lnx)dx+\int^{e}_{\frac{1}{e}}(lnx+1)dx\)
(Vì \(lnx-1<0, \forall x\in \left [ \frac{1}{e} ;1\right ]\) và \(-lnx-1<0, \forall x\in \left [ 1;e \right ]\))
\(\Rightarrow S=\int^{1}_{\frac{1}{e}}dx-\int^{1}_{\frac{1}{e}}lnx dx+ \int^{e}_{\frac{1}{e}}lnx dx +\int^{e}_{\frac{1}{e}}dx\)
\(=x\bigg|^{1}_{\frac{1}{e}}+\bigg|^{e}_{\frac{1}{e}} – \int_{\frac{1}{e}}^{e}ln xdx+\int_{1}^{e} ln xdx\)
\(=1-\frac{1}{e}+e-1-\int_{\frac{1}{e}}^{e} lnx dx+\int_{1}^{e}ln x dx\)
\(=e-\frac{1}{e}-x lnx \Bigg|^1_{\frac{1}{e}}+\int_{\frac{1}{e}}^{1}dx+xln \Bigg|^e_1-\int_{1}^{e}dx\)
\(=e-\frac{1}{e}-\frac{1}{e}+1-\frac{1}{e}+e-e+1=e-\frac{3}{e}+2\) (đvdt)
c) Xét phương trình: \((x-6)^2=6x-x^2\Leftrightarrow 2x^2-18x+36=0\)
\(\Leftrightarrow x=3;x=6\)
Do đó diện tích cần tìm là:
\(S=\int_{3}^{6} \left | (x-6)^2-(6x-x^2) \right |dx= \int_{3}^{6} \left | 2x^2-18x+36 \right |dx\)
\(=-2\int_{3}^{6}(x^2-9x+18)dx\)
(Vì: \(2x^2-18x+36 \leq 0\) khi \(3\leq x\leq 6\))
\(=-2\left ( \frac{x^3}{3}-\frac{9}{2}x^2+18x \right ) \bigg|^6_3=-2\left ( 8-\frac{45}{2} \right )=9\) (đvdt).
2. Giải bài 2 trang 123 sgk Giải tích 12
Tính diện tích hình phẳng giới hạn bởi đường cong y = x2 +1, tiếp tuyến với đường thẳng này tại điểm M(2;5) và trục Oy.
Bài giải:
Ta lập phương trình tiếp tuyến với \(y=x^2+1\) tại M ta có \(y’=2x\Rightarrow y'(2)=4.\) Do đó phương trình tiếp tuyến với \(y=x^2+1\) tại M(2;5) có phương trình là: \(y=4x-3\).

Vậy diện tích cần tìm là:
\(S=\int_{0}^{2}|x^{2}+1 -(4x+3)|dx =\int_{0}^{2}(x^{2}-4x+4)dx\)
\(=\left ( \frac{1}{3}x^3-2x^2+4x \right ) \Bigg|^2_0 =\frac{8}{3} -8 +8=\frac{8}{3}.\) (đvdt)
3. Giải bài 3 trang 123 sgk Giải tích 12
Parabol $y=\frac{x^{2}}{2}$ chia hình tròn có tâm tại gộc toạ độ, bán kính $2\sqrt{2}$ thành hai phần.
Tìm tỉ số diện tích của chúng.
Bài giải:

Từ hình vẽ ta có:
\(S_1=2 \int_{0}^{2} \left [ \sqrt{8-x^2}-\frac{x^2}{2} \right ] dx\)
\(=2 \int_{0}^{2} \sqrt{8-x^2}- \int_{0}^{2} x^2 dx\)
\(=2 \int_{0}^{2} \sqrt{8-x^2}dx-\frac{x^3}{3}\Bigg |^2_0\)
\(=2 \int_{0}^{2} \sqrt{8-x^2}dx-\frac{8}{3}\)
Đặt \(x=2\sqrt{2}sint\Rightarrow dx=2\sqrt{2}costdt\)
Khi x = 0 thì t = 0; khi x = 2 thì \(t=\frac{\pi }{4}\)
\(\Rightarrow 2\int_{0}^{2}\sqrt{8-x^2}dx=4\sqrt{2} \int_{0}^{\frac{\pi }{4}}\sqrt{8-8sin^2t}.cost dt\)
\(=16 \int_{0}^{\frac{\pi }{4}}cos^2t dt=8 \int_{0}^{\frac{\pi }{4}}(1+cos2t)dt=2\pi+4\)
\(\Rightarrow S_1=2\pi+4-\frac{8}{3}=\frac{6\pi+4}{3}\)
Gọi S là diện tích hình tròn tâm O bán kính \(R=2\sqrt{2}\) ta có \(S=8\pi .\)
Từ đó \(\Rightarrow S_2=S-S_1=8\pi-\frac{6\pi+4}{3}= \frac{18 \pi-4}{3}\)
Vậy \(\frac{S_2}{S_1}=\frac{18\pi -4}{6\pi+4}=\frac{9\pi-2}{3\pi+2}\)
4. Giải bài 4 trang 123 sgk Giải tích 12
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục Ox:
a) \(\small y = 1 – x^2 , y = 0\) ;
b) \(\small y = cosx, y = 0, x = 0, x = \pi\) ;
c) \(\small y = tanx, y = 0, x = 0,x=\frac{\pi }{4}\) ;
Bài giải:
a) Phương trình hoành độ giao điểm của hai đồ thị hàm số là: \(1 – x^2= 0 ⇔ x = ±1\).
Khi đó thể tích khối tròn xoay cần tìm là :
\(V=\pi \int_{-1}^{1}(1-x^{2})^{2}dx=2\pi \int_{0}^{1}(x^{4}-2x^{2}+1)dx\)
\(=2\pi \left (\frac{x^{5}}{5}- \frac{2}{3}x^{3}+x \right )|_{0}^{1}=2\pi\left ( \frac{1}{5}-\frac{2}{3}+1 \right )=\frac{16\pi}{15}.\)
b) Thể tích cần tìm là:
\(V= \pi \int_{0}^{\pi }cos^{2}xdx =\frac{\pi }{2}\int_{0}^{\pi}(1+cos2x)dx\)
\(=\frac{\pi }{2}\left (x+\frac{1}{2}sin2x \right )|_{0}^{\pi }=\frac{\pi }{2}.\pi =\frac{\pi ^{2}}{2}\)
c) Thể tích cần tìm là:
\(V=\pi\int_{0}^{\frac{\pi }{4}}tan^{2}xdx=\pi\int_{0}^{\frac{\pi }{4} }\left (\frac{1}{cos^{2}x}-1 \right )dx\)
\(=\pi \left (tanx-x \right )|_{0}^{\frac{\pi }{4}}=\pi (1-\frac{\pi }{4})\)
\(=\frac{\pi(4-\pi)}{4}\).
5. Giải bài 5 trang 123 sgk Giải tích 12
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt \(\widehat{POA}=\alpha\) và \(OM=R, \left ( 0\leq \alpha \leq \frac{\pi }{3}, R>0 \right )\).
Gọi \(v\) là khối tròn xoay thu được khi quay tam giác đó xung quanh Ox (H.63).
a) Tính thể tích của \(v\) theo α và R.
b) Tìm \(\small \alpha\) sao cho thể tích \(v\) là lớn nhất.

Bài giải:
a) Ta có: \(OP=R.cos\alpha ; PM=R.sin\alpha\)
⇒ Diện tích đáy B của khối tròn xoay V là: \(B= \pi .PM^2=\pi .R^2.sin^2\alpha .\)
Theo công thức (4) ta có thể tích của khối tròn xoay V là:
\(V=\frac{1}{3}B.OP=\frac{1}{3}.R.cos\alpha .\pi .R^2.sin^2\alpha\)
\(=\frac{1}{3}\pi .R^3.cos\alpha .sin^2\alpha =\frac{1}{3}\pi .R^3(cos\alpha -cos^3\alpha )\)
Với \(=\left ( 0\leq \alpha \leq \frac{\pi }{3} \right )\)
b) Ta có V lớn nhất \(\Leftrightarrow cos\alpha -cos^3\alpha\) lớn nhất.
Xét hàm số \(f(t)=t-t^3(t=cos\alpha )\). Khi \(\alpha \in \left ( 0;\frac{\pi }{3} \right )\) thì \(t \in \left ( \frac{1}{2};1\right )\)
Ta có: \(f'(t)=1-3t^2=0\Leftrightarrow t=\frac{1}{\sqrt{3}} \ \ \left (\frac{1}{2}
Ta có bảng biến thiên:

⇒ $f(t)$ lớn nhất bằng \(\frac{2}{3\sqrt{3}}\) khi \(t=\frac{1}{\sqrt{3}}\)
Hay \(cos \alpha -cos^3\alpha\) lớn nhất: \(\frac{2}{3\sqrt{3}}\) đạt được khi \(cos\alpha =\frac{1}{\sqrt{3}}\)
Vậy \(V_{max}=\frac{2\pi \sqrt{3}}{27}R^3\) khi \(cos\alpha =\frac{1}{\sqrt{3}}\).
Bài trước:
Bài tiếp theo:
- Ôn tập chương 3: Giải bài 1 2 3 4 5 6 7 trang 128 129 sgk Giải tích 12
- Ôn tập chương 3: Giải bài tập trắc nghiệm 1 2 3 4 5 6 trang 129 130 sgk Giải tích 12
Xem thêm:
- Các bài toán 12 khác
- Để học tốt môn Vật lí lớp 12
- Để học tốt môn Sinh học lớp 12
- Để học tốt môn Ngữ văn lớp 12
- Để học tốt môn Lịch sử lớp 12
- Để học tốt môn Địa lí lớp 12
- Để học tốt môn Tiếng Anh lớp 12
- Để học tốt môn Tiếng Anh lớp 12 thí điểm
- Để học tốt môn Tin học lớp 12
- Để học tốt môn GDCD lớp 12
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 12 với giải bài 1 2 3 4 5 trang 123 sgk Giải tích 12!
“Bài tập nào khó đã có giaibaisgk.com“
