Hướng dẫn Giải bài 1 2 3 4 5 6 trang 114 115 sgk Giải tích 12

Nội Dung

Hướng dẫn giải Bài §2. Tích phân, Chương 3. Nguyên hàm – Tích phân và ứng dụng, sách giáo khoa Giải tích 12. Nội dung bài giải bài 1 2 3 4 5 6 trang 114 115 sgk Giải tích 12 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập giải tích có trong SGK để giúp các em học sinh học tốt môn toán lớp 12.

Lý thuyết

1. Tích phân

Cho hàm $f(x)$ liên tục trên khoảng K và a, b là hai số bất kỳ thuộc K. Nếu $F(x)$ là một nguyên hàm của $f(x)$ thì hiệu số $F(b)-F(a)$ được gọi là tích phân của $f(x)$ từ a đến b.

Ký hiệu là $\int\limits_a^b {f(x)dx} .$

Công thức: $\displaystyle \int \limits_{a}^{b} f_{(x)} dx = F_{(x)}|_a^b = F_{(b)} -F_{(a)}$

2. Tính chất của tích phân:

Cho các hàm số $f(x),\,g(x)$ liên tục trên K và $a,b,c$ là ba số thuộc $K$.

$\,\int\limits_a^a {f(x)dx = 0}$

$\int\limits_a^b {f(x)dx = – \int\limits_b^a {f(x)dx} }$

$\int\limits_a^b {f(x)dx = \int\limits_a^c {f(x)dx} + \int\limits_c^b {f(x)dx} }$

$\int\limits_a^b {k.f(x)dx = k\int\limits_a^b {f(x)dx} }$

$\int\limits_a^b {[f(x) \pm g(x)]dx = \int\limits_a^b {f(x)dx} \pm \int\limits_a^b {g(x)dx} }$

3. Phương pháp tính tích phân

a) Phương pháp đổi biến số

Công thức đổi biến số $\int\limits_a^b {f[u(x)]u'(x)dx = \int\limits_{u(a)}^{u(b)} {f(u)du} }.$ Trong đó $f(x)$ là hàm số liên tục và $u(x)$ có đạo hàm liên tục trên khoảng J sao cho hàm hợp $f[u(x)]$ xác định trên J; $a,\,b \in J.$

Các phương pháp đổi biến số thường gặp:

♦ Cách 1: Đặt $u = u(x)$ ($u$ là một hàm theo $x$).

♦ Cách 2: Đặt $x=x(t)$ ($x$ là một hàm theo $t$).

b) Phương pháp tích phân từng phần

Định lí: Nếu $u(x),\,v(x)$ là hai hàm số có đạo hàm liên tục trên khoảng K và $a,b$ là hai số thuộc K thì $\int\limits_a^b {u(x)v'(x)dx} = \left. {u(x)v(x)} \right|_a^b – \int\limits_a^b {v(x)u'(x)dx}.$

Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong phần hoạt động của học sinh sgk Giải tích 12.

Câu hỏi

1. Trả lời câu hỏi 1 trang 103 sgk Giải tích 12

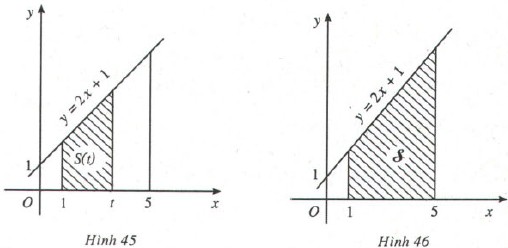
Kí hiệu $T$ là hình thang vuông giới hạn bởi đường thẳng $y = 2x + 1$, trục hoành và hai đường thẳng $x = 1, x = t (1 ≥ t ≥ 5)$ (H.45).

1. Tính diện tích $S$ của hình $T$ khi $t = 5$ (H.46).

2. Tính diện tích $S(t)$ của hình $T$ khi $x ∈ [1; 5]$.

3. Chứng minh rằng $S(t)$ là một nguyên hàm của $f(t)=2t+1, t\in [1;5]$ và diện tích $S=S(5)-S(1)$.

Trả lời:

1. (Hình 46)

Kí hiệu $A$ là điểm có tọa độ $(1,0), D$ là điểm có tọa độ $(5,0). B, C$ lần lượt là giao điểm của đường thẳng $x = 1$ và $x = 5$ với đường thẳng $y = 2x + 1$.

Khi đó $B$ và $C$ sẽ có tọa độ lần lượt là $(1,3)$ và $(5,11)$.

Ta có: $AB = 3, CD = 11, AD = 4$.

⇒ Diện tích hình thang:

$\displaystyle ABCD = {{(AB + CD).AD} \over 2} = 28$

2. (Hình 45)

Kí hiệu $A$ là điểm có tọa độ $(1,0), D$ là điểm có tọa độ $(5,0). B, C$ lần lượt là giao điểm của đường thẳng $x = 1$ và $x = t$ với đường thẳng $y = 2x + 1$.

Khi đó ta có $B(1,3)$ và $C(t, 2t + 1)$.

Ta có $AB = 3, AD = t – 1, CD = 2t + 1$.

⇒ Khi đó diện tích hình thang:

$\displaystyle S(t) = {{(AB + CD).AD} \over 2} = {{(3 + 2t + 1).(t – 1)} \over 2} $ $= {t^2} + t – 2$

Do đó $S(t)= {t^2} + t – 2$

3. Vì $S'(t)= ({t^2} + t – 2)’$ $=2t+1$ nên hàm số $S(t)$ là một nguyên hàm của hàm số $f(t)=2t+1, t\in [1;5]$.

Dễ thấy $S(5)-S(1)=\left( {{5^2} + 5 – 2} \right) – \left( {{1^2} + 1 – 2} \right) = 28 = S$ hay $S=S(5)-S(1)$.

2. Trả lời câu hỏi 2 trang 106 sgk Giải tích 12

Giả sử $f(x)$ là hàm số liên tục trên đoạn $[a; b], F(x)$ và $G(x)$ là hai nguyên hàm của $f(x)$. Chứng minh rằng $F(b) – F(a) = G(b) – G(a)$, (tức là hiệu số $F(b) – F(a)$ không phụ thuộc việc chọn nguyên hàm).

Trả lời:

Vì $F(x)$ và $G(x)$ đều là nguyên hàm của $f(x)$ nên tồn tại một hằng số $C$ sao cho: $F(x) = G(x) + C$

Khi đó:

$F(b) – F(a) = G(b) + C – G(a) – C = G(b) – G(a).$

3. Trả lời câu hỏi 3 trang 108 sgk Giải tích 12

Hãy chứng minh các tính chất 1 và 2.

Trả lời:

♦ Cách 1:

– Tính chất 1:

+) Nếu $k = 0$ thì tính chất đúng.

+) Nếu $k \ne 0$ thì $\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx} = F\left( x \right)$ $ \Rightarrow \int {f\left( x \right)dx} = \dfrac{{F\left( x \right)}}{k}$

Do đó $\int\limits_a^b {kf\left( x \right)dx} = \left. {F\left( x \right)} \right|_a^b = F\left( b \right) – F\left( a \right)$ và $k\int\limits_a^b {f\left( x \right)dx} = k.\left. {\dfrac{{F\left( x \right)}}{k}} \right|_a^b$ $ = F\left( b \right) – F\left( a \right)$

Từ đó suy ra $\int\limits_a^b {kf\left( x \right)dx} = k\int\limits_a^b {f\left( x \right)dx} $.

– Tính chất 2:

Giả sử $F\left( x \right),G\left( x \right)$ lần lượt là các nguyên hàm của hai hàm số $f\left( x \right),g\left( x \right)$.

Ta có: $\int {\left[ {f\left( x \right) \pm g\left( x \right)} \right]dx} = \int {f\left( x \right)dx} \pm \int {g\left( x \right)dx} $ $ = F\left( x \right) \pm G\left( x \right)$

Khi đó $\int\limits_a^b {\left[ {f\left( x \right) \pm g\left( x \right)} \right]dx} = \left. {\left[ {F\left( x \right) \pm G\left( x \right)} \right]} \right|_a^b$ $ = \left[ {F\left( b \right) \pm G\left( b \right)} \right] – \left[ {F\left( a \right) \pm G\left( a \right)} \right]$ $ = \left[ {F\left( b \right) – F\left( a \right)} \right] \pm \left[ {G\left( b \right) – G\left( a \right)} \right]$.

Lại có $\int\limits_a^b {f\left( x \right)dx} \pm \int\limits_a^b {g\left( x \right)dx} $ $ = \left. {F\left( x \right)} \right|_a^b \pm \left. {G\left( x \right)} \right|_a^b$ $ = \left[ {F\left( b \right) – F\left( a \right)} \right] \pm \left[ {G\left( b \right) – G\left( a \right)} \right]$.

Từ đó ta có điều phải chứng minh.

♦ Cách 2:

4. Trả lời câu hỏi 4 trang 110 sgk Giải tích 12

Cho tích phân $I = \int\limits_0^1 {{{(2x + 1)}^2}} dx$

1. Tính $I$ bằng cách khai triển ${\left( {2x{\rm{ }} + 1} \right)^2}$

2. Đặt $u = 2x + 1$. Biến đổi biểu thức ${\left( {2x{\rm{ }} + 1} \right)^2}dx$ thành $g(u)du$.

3. Tính $\int\limits_{u(0)}^{u(1)} {g(u)du} $ và so sánh kết quả với $I$ trong câu 1.

Trả lời:

1. Ta có:

$\displaystyle \eqalign{
& I = \int\limits_0^1 {{{(2x + 1)}^2}} dx = \int\limits_0^1 {\left( {4{x^2} + 4x + 1} \right)} dx \cr
& = ({4 \over 3}{x^3} + 2{x^2} + x)|_0^1 = {{13} \over 3} \cr} $

2. Vì $u = 2x + 1$ nên $du = 2dx$. Ta có:

$\displaystyle{(2x + 1)^2}dx = {u^2}{{du} \over 2}$

3. $u(1) = 3; u(0) = 1$. Ta có:

$\displaystyle\int\limits_{u(0)}^{u(1)} {g(u)du = \int\limits_1^3 {{u^2}{{du} \over 2}} } = {{{u^3}} \over 6}|_1^3 = {{13} \over 3}$

Vậy $\displaystyle I = {{13} \over 3}$

5. Trả lời câu hỏi 5 trang 112 sgk Giải tích 12

a) Hãy tính $\smallint {\rm{ }}\left( {x{\rm{ }} + {\rm{ }}1} \right){e^x}dx$ bằng phương pháp tính nguyên hàm từng phần.

b) Từ đó tính $\int\limits_0^1 {(x + 1){e^x}dx} $

Trả lời:

a) Đặt $\left\{ \begin{array}{l}u = x + 1\\dv = {e^x}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = {e^x}\end{array} \right.$ $ \Rightarrow \int {\left( {x + 1} \right){e^x}dx} = \left( {x + 1} \right){e^x} – \int {{e^x}dx} $ $ = \left( {x + 1} \right){e^x} – {e^x} + C$ $ = x{e^x} + C$

b) Vì $F(x)=xe^x$ là một nguyên hàm của hàm số $f(x)=(x+1)e^x$ nên

$\int\limits_0^1 {\left( {x + 1} \right){e^x}dx} = \left. {x{e^x}} \right|_0^1 $ $= 1.{e^1} – 0.{e^0} = e$

Dưới đây là Hướng dẫn giải bài 1 2 3 4 5 6 trang 114 115 sgk Giải tích 12. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập giải tích 12 kèm bài giải chi tiết bài 1 2 3 4 5 6 trang 114 115 sgk Giải tích 12 của Bài §2. Tích phân của hàm số trong Chương 3. Nguyên hàm – Tích phân và ứng dụng cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 6 trang 114 115 sgk Giải tích 12

1. Giải bài 1 trang 114 sgk Giải tích 12

Tính các tích phân sau:

a)$\int_{\frac{-1}{2}}^{\frac{1}{2}}\sqrt[3]{ (1-x)^{2}}dx$ b) $\int_{0}^{\frac{\pi}{2}}sin(\frac{\pi}{4}-x)dx$

c)$\int_{\frac{1}{2}}^{2}\frac{1}{x(x+1)}dx$ d) $\int_{0}^{2}x(x+1)^{2}dx$

e)$\int_{\frac{1}{2}}^{2}\frac{1-3x}{(x+1)^{2}}dx$ g) $\int_{\frac{-\pi}{2}}^{\frac{\pi}{2}}sin3xcos5xdx$

Bài giải:

a) Ta có:

$\begin{array}{l} \,\,\,\int\limits_{ – \frac{1}{2}}^{\frac{1}{2}} {\sqrt[3]{{{{\left( {1 – x} \right)}^2}}}dx} = \int\limits_{ – \frac{1}{2}}^{\,\frac{1}{2}} {{{\left( {1 – x} \right)}^{\frac{2}{3}}}dx} \\= \left. { – 1.\frac{{{{\left( {1 – x} \right)}^{\frac{5}{3}}}}}{{\frac{5}{3}}}} \right|_{ – \frac{1}{2}}^{\frac{1}{2}} = – \frac{3}{5}.\left[ {{{\left( {\frac{1}{2}} \right)}^{\frac{5}{3}}} – {{\left( {\frac{3}{2}} \right)}^{\frac{5}{3}}}} \right]\\= – \frac{3}{5}\left[ {\frac{1}{{\sqrt[3]{{{2^5}}}}} – \frac{{\sqrt[3]{{{3^5}}}}}{{\sqrt[3]{{{2^5}}}}}} \right] = – \frac{3}{5}\left[ {\frac{1}{{\sqrt[3]{{{2^3}{{.2}^2}}}}} – \frac{{\sqrt[3]{{{3^3}{{.3}^2}}}}}{{\sqrt[3]{{{2^3}{{.2}^2}}}}}} \right]\\= – \frac{3}{5}\left[ {\frac{1}{{2\sqrt[3]{4}}} – \frac{{3\sqrt[3]{9}}}{{2\sqrt[3]{4}}}} \right] = \frac{3}{{10\sqrt[3]{4}}}\left( {3\sqrt[3]{9} – 1} \right)\end{array}$

b) Ta có:

$\,\,\int\limits_0^{\frac{\pi }{2}} {\sin \left( {\frac{\pi }{4} – x} \right)dx} = \left. {\cos \left( {\frac{\pi }{4} – x} \right)} \right|_0^{\frac{\pi }{2}} = \cos \left( { – \frac{\pi }{4}} \right) – \cos \frac{\pi }{4} = 0$

c) Ta có: $\frac{1}{{x\left( {x + 1} \right)}} = \frac{1}{x} – \frac{1}{{x + 1}}$

$\begin{array}{l}\Rightarrow \int\limits_{\frac{1}{2}}^2 {\frac{1}{{x\left( {x + 1} \right)}}dx} = \int\limits_{\frac{1}{2}}^2 {\left( {\frac{1}{x} – \frac{1}{{x + 1}}} \right)dx} \\= \left. {\left( {\ln \left| x \right| – \ln \left| {x + 1} \right|} \right)} \right|_{\frac{1}{2}}^2 = \left. {\ln \left| {\frac{x}{{x + 1}}} \right|} \right|_{\frac{1}{2}}^2\\= \ln \frac{2}{3} – \ln \frac{1}{3} = \ln \left( {\frac{2}{3}:\frac{1}{3}} \right) = \ln 2\end{array}$.

d) Ta có:

$\begin{array}{l}\,\,x{\left( {x + 1} \right)^2} = x\left( {{x^2} + 2x + 1} \right) = {x^3} + 2{x^2} + x\\\Rightarrow \int\limits_0^2 {x{{\left( {x + 1} \right)}^2}dx} = \int\limits_0^2 {\left( {{x^3} + 2{x^2} + x} \right)dx} \\= \left. {\left( {\frac{{{x^4}}}{4} + 2\frac{{{x^3}}}{3} + \frac{{{x^2}}}{2}} \right)} \right|_0^2 = \frac{{34}}{3}\end{array}$

e) Ta có:

$\begin{array}{l}\,\,\frac{{1 – 3x}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{ – 3\left( {x + 1} \right) + 4}}{{{{\left( {x + 1} \right)}^2}}} = – \frac{3}{{x + 1}} + \frac{4}{{{{\left( {x + 1} \right)}^2}}}\\\Rightarrow \int\limits_{\frac{1}{2}}^2 {\frac{{1 – 3x}}{{{{\left( {x + 1} \right)}^2}}}dx} = \int\limits_{\frac{1}{2}}^2 {\left( { – \frac{3}{{x + 1}} + \frac{4}{{{{\left( {x + 1} \right)}^2}}}} \right)dx} \\= – 3\int\limits_{\frac{1}{2}}^2 {\frac{{dx}}{{x + 1}}} + 4\int\limits_{\frac{1}{2}}^2 {\frac{{dx}}{{{{\left( {x + 1} \right)}^2}}}} \\= – \left. {3\ln \left| {x + 1} \right|} \right|_{\frac{1}{2}}^2 – \left. {\frac{4}{{x + 1}}} \right|_{\frac{1}{2}}^2\\= – 3\left( {\ln 3 – \ln \frac{3}{2}} \right) – 4\left( {\frac{1}{3} – \frac{2}{3}} \right)\\= – 3\ln 2 + \frac{4}{3}\end{array}$

g) ♦ Cách 1:

Đặt $f(x) = sin3xcos5x$ ta có: $f\left( { – x} \right) = \sin \left( { – 3x} \right)\cos \left( { – 5x} \right) = – \sin 3x\cos 5x = – f\left( x \right) \Rightarrow $ là hàm số lẻ, từ đó ta có: $\int\limits_{ – \frac{\pi }{2}}^{\frac{\pi }{2}} {\sin 3x\cos 5xdx} = 0$.

♦ Cách 2:

$\begin{array}{l}\sin 3x\cos 5x = \frac{1}{2}\left( {\sin 8x – \sin 2x} \right)\\\Rightarrow \int\limits_{ – \frac{\pi }{2}}^{\frac{\pi }{2}} {\sin 3x\cos 5xdx} = \frac{1}{2}\int\limits_{ – \frac{\pi }{2}}^{\frac{\pi }{2}} {\left( {\sin 8x – \sin 2x} \right)dx} \\= \frac{1}{2}\left. {\left( { – \frac{{\cos 8x}}{8} + \frac{{\cos 2x}}{2}} \right)} \right|_{ – \frac{\pi }{2}}^{\frac{\pi }{2}}\\= \frac{1}{2}\left( { – \frac{5}{8} – \left( { – \frac{5}{8}} \right)} \right) = 0\end{array}$

2. Giải bài 2 trang 114 sgk Giải tích 12

Tính các tích phân sau:

a) $\int_0^2 {\left| {1 – x} \right|} dx$ b) $\int_0^{{\pi \over 2}} s i{n^2}xdx$

c) $\int_0^{ln2} {{{{e^{2x + 1}} + 1} \over {{e^x}}}} dx$ d) $\int_0^\pi s in2xco{s^2}xdx$

Bài giải:

a) Ta có: $\left| {1 – x} \right| = \left[ \begin{array}{l}1 – x\,\,khi\,\,x \le 1\\x – 1\,\,khi\,\,x > 1\end{array} \right.$

$\Rightarrow \int_0^2 {\left| {1 – x} \right|} dx = \int_0^1 {\left| {1 – x} \right|} dx + \int_1^2 {\left| {1 – x} \right|} dx$

$= \int_0^1 {(1 – x)} dx + \int_1^2 {(x – 1)} dx$

$ = \left. {\left( {x – \dfrac{{{x^2}}}{2}} \right)} \right|_0^1 + \left. {\left( {\dfrac{{{x^2}}}{2} – x} \right)} \right|_1^2 = \dfrac{1}{2} + \dfrac{1}{2} = 1$

b) Ta có:

$\begin{array}{l}\,\,\int\limits_0^{\frac{\pi }{2}} {{{\sin }^2}xdx} = \dfrac{1}{2}\int\limits_0^{\frac{\pi }{2}} {\left( {1 – \cos 2x} \right)dx} \\= \dfrac{1}{2}\left. {\left( {x – \dfrac{{\sin 2x}}{2}} \right)} \right|_0^{\frac{\pi }{2}}\\= \dfrac{1}{2}.\dfrac{\pi }{2} = \dfrac{\pi }{4}\end{array}$

c) Ta có:

$\begin{array}{l}\,\,\int\limits_0^{\ln 2} {\dfrac{{{e^{2x + 1}} + 1}}{{{e^x}}}dx} = \int\limits_0^{\ln 2} {\left( {{e^{2x + 1 – x}} + {e^{ – x}}} \right)dx} \\= \int\limits_0^{\ln 2} {\left( {{e^{x + 1}} + {e^{ – x}}} \right)dx} \\= \left. {\left( {{e^{x + 1}} – {e^{ – x}}} \right)} \right|_0^{\ln 2}\\= {e^{\ln 2 + 1}} – {e^{ – \ln 2}} – \left( {e – 1} \right)\\= {e^{\ln 2}}.e – \dfrac{1}{2} – e + 1\\= e + \dfrac{1}{2}\end{array}$

d) Ta có:

$\begin{array}{l}\,\,\sin 2x\cos 2x = \sin 2x\dfrac{{1 + \cos 2x}}{2}\\\,\,\, = \dfrac{1}{2}\sin 2x + \dfrac{1}{2}\sin 2x\cos 2x = \dfrac{1}{2}\sin 2x + \dfrac{1}{4}\sin 4x\\\Rightarrow \int\limits_0^\pi {\sin 2x\cos 2xdx} = \int\limits_0^\pi {\left( {\dfrac{1}{2}\sin 2x + \dfrac{1}{4}\sin 4x} \right)dx} \\= \left. {\left( { – \dfrac{1}{4}\cos 2x – \dfrac{1}{{16}}\cos 4x} \right)} \right|_0^\pi \\= – \dfrac{1}{4} – \dfrac{1}{{16}} – \left( { – \dfrac{1}{4} – \dfrac{1}{{16}}} \right) = 0\end{array}$

3. Giải bài 3 trang 115 sgk Giải tích 12

Sử dụng phương pháp đổi biến số, hãy tính:

a) $\int_{0}^{3}\frac{x^{2}}{(1+x)^{\frac{3}{2}}}dx$ (Đặt $u= x+1$);

b) $\int_{0}^{1}\sqrt{1-x^{2}}dx$ (Đặt $x = sint$ );

c) $\int_{0}^{1}\frac{e^{x}(1+x)}{1+x.e^{x}}dx$ (Đặt $u = 1 + x.{e^x}$);

d) $\int_{0}^{\frac{a}{2}}\frac{1}{\sqrt{a^{2}-x^{2}}}dx$ (Đặt $x= asint$).

Bài giải:

a) Đặt $u= x+1 \Rightarrow du = dx$ và $x = u – 1$.

Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow u = 1\\x = 3 \Rightarrow u = 4\end{array} \right.$

$\begin{array}{l}\int\limits_0^3 {\frac{{{x^2}}}{{{{\left( {1 + x} \right)}^{\frac{3}{2}}}}}dx} = \int\limits_1^4 {\frac{{{{\left( {u – 1} \right)}^2}}}{{{u^{\frac{3}{2}}}}}du} = \int\limits_1^4 {\frac{{{u^2} – 2u + 1}}{{{u^{\frac{3}{2}}}}}du} \\= \int\limits_1^4 {\left( {{u^{\frac{1}{2}}} – 2{u^{ – \frac{1}{2}}} + {u^{ – \frac{3}{2}}}} \right)du} \\= \left. {\left( {\frac{2}{3}{u^{\frac{3}{2}}} – 4{u^{\frac{1}{2}}} – 2{u^{ – \frac{1}{2}}}} \right)} \right|_1^4\\= – \frac{{11}}{3} – \left( { – \frac{{16}}{3}} \right) = \frac{5}{3}\end{array}$

b) Đặt $x = sint$, $0<t<\frac{\pi}{2}$.

Ta có: $dx = costdt$ và $\sqrt{1-x^{2}}=\sqrt{1-sin^{2}t}= \sqrt{cos^{2}t}=\left | cost \right |= cos t.$

Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow t = 0\\x = 1 \Rightarrow t = \frac{\pi }{2}\end{array} \right.$

$\begin{array}{l}\Rightarrow \int\limits_0^1 {\sqrt {1 – {x^2}} dx} = \int\limits_0^{\frac{\pi }{2}} {\sqrt {1 – {{\sin }^2}t} \cos tdt} \\= \int\limits_0^{\frac{\pi }{2}} {{{\cos }^2}tdt} = \frac{1}{2}\int\limits_0^{\frac{\pi }{2}} {\left( {1 + \cos 2t} \right)dt} \\= \frac{1}{2}\left. {\left( {t + \frac{{\sin 2t}}{2}} \right)} \right|_0^{\frac{\pi }{2}}\\= \frac{1}{2}.\frac{\pi }{2} = \frac{\pi }{4}\end{array}$

c) Đặt: $t = 1 + x.{e^x} \Rightarrow dt = \left( {{e^x} + x.{e^x}} \right)dx = {e^x}\left( {1 + x} \right)dx$.

Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow t = 1\\x = 1 \Rightarrow t = 1 + e\end{array} \right.$

$\begin{array}{l}\Rightarrow \int\limits_0^1 {\frac{{{e^x}\left( {1 + x} \right)}}{{1 + x{e^x}}}dx} = \int\limits_1^{1 + e} {\frac{{dt}}{t}} = \left. {\ln \left| t \right|} \right|_1^{1 + e}\\= \ln \left( {1 + e} \right) – \ln 1 = \ln \left( {1 + e} \right)\end{array}$

d) Đặt $x = a\sin t \Rightarrow dx = a\cos tdt$

Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow t = 0\\x = \frac{a}{2} \Rightarrow t = \frac{\pi }{6}\end{array} \right.$

$\begin{array}{l}\Rightarrow \int\limits_0^{\frac{a}{2}} {\frac{1}{{\sqrt {{a^2} – {x^2}} }}dx} = \int\limits_0^{\frac{\pi }{6}} {\frac{{a\cos tdt}}{{\sqrt {{a^2} – {a^2}{{\sin }^2}t} }}} \\= \int\limits_0^{\frac{\pi }{6}} {\frac{{a\cos tdt}}{{a.\cos t}}} = \int\limits_0^{\frac{\pi }{6}} {dt} = \left. t \right|_0^{\frac{\pi }{6}} = \frac{\pi }{6}\end{array}$.

4. Giải bài 4 trang 115 sgk Giải tích 12

Sử dụng phương pháp tích phân từng phần, hãy tính tích phân:

a) $\int_{0}^{\frac{\pi}{2}}(x+1)sinxdx$ ;

b) $\int_{1}^{e}x^{2}lnxdx$

c) $\int_{0}^{1}ln(1+x))dx$ ;

d) $\int_{0}^{1}(x^{2}-2x+1)e^{-x}dx$.

Bài giải:

a) Đặt $\left\{ \begin{array}{l}u = x + 1\\dv = \sin xdx\end{array} \right.$ $ \Rightarrow \left\{ \begin{array}{l}du = dx\\v = – \cos x\end{array} \right.$

$\begin{array}{l}\Rightarrow \int\limits_0^{\frac{\pi }{2}} {\left( {x + 1} \right)\sin xdx} = \left. { – \left( {x + 1} \right)\cos x} \right|_0^{\frac{\pi }{2}} + \int\limits_0^{\frac{\pi }{2}} {\cos xdx} \\= \left. { – \left( {x + 1} \right)\cos x} \right|_0^{\frac{\pi }{2}} + \left. {\sin x} \right|_0^{\frac{\pi }{2}}\\= 1 + 1 = 2\end{array}$.

b) Đặt $\left\{ \begin{array}{l}u = \ln x\\dv = {x^2}dx\end{array} \right.$ $ \Rightarrow \left\{ \begin{array}{l}du = \frac{{dx}}{x}\\v = \frac{{{x^3}}}{3}\end{array} \right.$

$\begin{array}{l}\Rightarrow \int\limits_1^e {{x^2}\ln x} dx = \left. {\left( {\ln x.\frac{{{x^3}}}{3}} \right)} \right|_1^e – \frac{1}{3}\int\limits_1^e {{x^2}dx} \\= \left. {\left( {\ln x.\frac{{{x^3}}}{3}} \right)} \right|_1^e – \left. {\frac{{{x^3}}}{9}} \right|_1^e\\= \frac{{{e^3}}}{3} – \left( {\frac{{{e^3}}}{9} – \frac{1}{9}} \right) = \frac{{2{e^3}}}{9} + \frac{1}{9} = \frac{1}{9}\left( {2{e^3} + 1} \right)\end{array}$

c) Đặt $\left\{ \begin{array}{l}u = \ln \left( {1 + x} \right)\\dv = dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = \frac{{dx}}{{1 + x}}\\v = x\end{array} \right.$

$\begin{array}{l}\Rightarrow \int\limits_0^1 {\ln \left( {x + 1} \right)dx} = \left. {\left( {x.\ln \left( {1 + x} \right)} \right)} \right|_0^1 – \int\limits_0^1 {\frac{x}{{x + 1}}dx} \\= \left. {\left( {x.\ln \left( {1 + x} \right)} \right)} \right|_0^1 – \int\limits_0^1 {\frac{{x + 1 – 1}}{{x + 1}}dx} \\= \left. {\left( {x.\ln \left( {1 + x} \right)} \right)} \right|_0^1 – \int\limits_0^1 {\left( {1 – \frac{1}{{x + 1}}} \right)dx} \\= \left. {\left( {x.\ln \left( {1 + x} \right)} \right)} \right|_0^1 – \left. {\left( {x – \ln \left| {x + 1} \right|} \right)} \right|_0^1\\= \ln 2 – \left( {1 – \ln 2} \right) = 2\ln 2 – 1\end{array}$

d) Đặt $\left\{ \begin{array}{l}u = {x^2} – 2x + 1\\dv = {e^{ – x}}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = \left( {2x – 2} \right)dx\\v = – {e^{ – x}}\end{array} \right.$

$\begin{array}{l}\Rightarrow \int\limits_0^1 {\left( {{x^2} – 2x – 1} \right){e^{ – x}}dx} = \left. { – {e^{ – x}}\left( {{x^2} – 2x – 1} \right)} \right|_0^1 + 2\int\limits_0^1 {\left( {x – 1} \right){e^{ – x}}dx} \\= \left. { – {e^{ – x}}\left( {{x^2} – 2x – 1} \right)} \right|_0^1 + 2{I_1}\\= 2{e^{ – 1}} – 1 + 2{I_1}\end{array}$

Đặt $\left\{ \begin{array}{l}u = x – 1\\dv = {e^{ – x}}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\dv = – {e^{ – x}}\end{array} \right.$.

$\begin{array}{l}\Rightarrow {I_1} = \left. { – {e^{ – x}}\left( {x – 1} \right)} \right|_0^1 + \int\limits_0^1 {{e^{ – x}}dx} \\= \left. { – {e^{ – x}}\left( {x – 1} \right)} \right|_0^1\left. { – {e^{ – x}}} \right|_0^1\\= – 1 – \left( {{e^{ – 1}} – 1} \right) =- {e^{ – 1}}\end{array}$.

Vậy $I = 2{e^{ – 1}} – 1 – 2{e^{ – 1}} = – 1$.

5. Giải bài 5 trang 115 sgk Giải tích 12

Tính các tích phân sau:

a) $\int_{0}^{1}(1+3x)^{\frac{3}{2}}dx$ ;

b) $\int_{0}^{\frac{1}{2}}\frac{x^{3}-1}{x^{2}-1}dx$

c) $\int_{1}^{2}\frac{ln(1+x)}{x^{2}}dx$

Bài giải:

a) Ta có:

$\begin{array}{l}\,\,\int\limits_0^1 {{{\left( {1 + 3x} \right)}^{\frac{3}{2}}}dx} = \left. {\dfrac{1}{3}.\dfrac{{{{\left( {1 + 3x} \right)}^{\frac{3}{2} + 1}}}}{{\frac{3}{2} + 1}}} \right|_0^1\\= \left. {\dfrac{2}{{15}}.{{\left( {1 + 3x} \right)}^{\frac{5}{2}}}} \right|_0^1 = \dfrac{2}{{15}}\left( {{4^{\frac{5}{2}}} – 1} \right) = \dfrac{2}{{15}}.31 = \dfrac{{62}}{{15}}\end{array}$

b) Ta có:

$\begin{array}{l}\,\,\,\int\limits_0^{\frac{1}{2}} {\dfrac{{{x^3} – 1}}{{{x^2} – 1}}dx} = \int\limits_0^{\frac{1}{2}} {\dfrac{{\left( {x – 1} \right)\left( {{x^2} + x + 1} \right)}}{{\left( {x – 1} \right)\left( {x + 1} \right)}}dx} \\= \int\limits_0^{\frac{1}{2}} {\dfrac{{{x^2} + x + 1}}{{x + 1}}dx} = \int\limits_0^{\frac{1}{2}} {\dfrac{{x\left( {x + 1} \right) + 1}}{{x + 1}}dx} \\= \int\limits_0^{\frac{1}{2}} {\left( {x + \dfrac{1}{{x + 1}}} \right)dx} = \left. {\left( {\dfrac{{{x^2}}}{2} + \ln \left| {x + 1} \right|} \right)} \right|_0^{\frac{1}{2}}\\= \dfrac{1}{8} + \ln \dfrac{3}{2}\end{array}$

c) Đặt $\left\{ \begin{array}{l}u = \ln \left( {1 + x} \right)\\dv = \dfrac{1}{{{x^2}}}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = \dfrac{1}{{1 + x}}dx\\v = – \dfrac{1}{x}\end{array} \right.$

$\begin{array}{l}\Rightarrow \int\limits_1^2 {\dfrac{{\ln \left( {1 + x} \right)}}{{{x^2}}}dx} = \left. { – \dfrac{1}{x}\ln \left( {1 + x} \right)} \right|_1^2 + \int\limits_1^2 {\dfrac{{dx}}{{x\left( {1 + x} \right)}}} \\= – \dfrac{1}{2}\ln 3 + \ln 2 + \int\limits_1^2 {\left( {\dfrac{1}{x} – \dfrac{1}{{1 + x}}} \right)dx} \\= – \dfrac{1}{2}\ln 3 + \ln 2 + \left. {\ln \left| {\dfrac{x}{{1 + x}}} \right|} \right|_1^2\\= – \dfrac{1}{2}\ln 3 + \ln 2 + \ln \dfrac{2}{3} – \ln \dfrac{1}{2}\\= \ln \dfrac{1}{{\sqrt 3 }} + \ln 2 + \ln \dfrac{2}{3} – \ln \dfrac{1}{2} = \ln \dfrac{{8\sqrt 3 }}{9}\end{array}$

6. Giải bài 6 trang 115 sgk Giải tích 12

Tính tích phân $\int_{0}^{1}x(1-x)^{5}dx$ bằng hai phương pháp:

a) Đổi biến số: $u = 1 – x$;

b) Tính tích phân từng phần.

Bài giải:

a) Đặt $u = 1 – x \Rightarrow x = 1 – u \Rightarrow dx = – du$.

Đổi cận: $\left\{ \begin{array}{l}x = 0 \Rightarrow u = 1\\x = 1 \Rightarrow u = 0\end{array} \right.$

$\begin{array}{l}\Rightarrow \int\limits_0^1 {x{{\left( {1 – x} \right)}^5}dx} = – \int\limits_1^0 {\left( {1 – u} \right){u^5}du} \\= \int\limits_0^1 {\left( {{u^5} – {u^6}} \right)du} = \left. {\left( {\dfrac{{{u^6}}}{6} – \dfrac{{{u^7}}}{7}} \right)} \right|_0^1 = \dfrac{1}{6} – \dfrac{1}{7} = \dfrac{1}{{42}}\end{array}$

b) Đặt $\left\{ \begin{array}{l}u = x\\dv = {\left( {1 – x} \right)^5}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = – \dfrac{{{{\left( {1 – x} \right)}^6}}}{6}\end{array} \right.$

$\begin{array}{l}\Rightarrow \int\limits_0^1 {x\left( {1 – {x^5}} \right)dx} = – x\left. {\dfrac{{{{\left( {1 – x} \right)}^6}}}{6}} \right|_0^1 + \dfrac{1}{6}\int\limits_0^1 {{{\left( {1 – x} \right)}^6}dx} \\= – \dfrac{1}{6}\left. {\dfrac{{{{\left( {1 – x} \right)}^7}}}{7}} \right|_0^1 = \dfrac{1}{{42}}
\end{array}$

Bài trước:

Giải bài 1 2 3 4 trang 102 103 sgk Giải tích 12

Bài tiếp theo:

Giải bài 1 2 3 4 5 trang 123 sgk Giải tích 12

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 12 với giải bài 1 2 3 4 5 6 trang 114 115 sgk Giải tích 12!

“Bài tập nào khó đã có giaibaisgk.com“