Nội Dung
Hướng dẫn giải Bài §1. Lũy thừa, Chương 2. Hàm số lũy thừa. Hàm số mũ và Hàm số lôgarit, sách giáo khoa Giải tích 12. Nội dung bài giải bài 1 2 3 4 5 trang 56 57 sgk Giải tích 12 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập giải tích có trong SGK để giúp các em học sinh học tốt môn toán lớp 12.
Lý thuyết
1. Khái niệm lũy thừa
a) Lũy thừa với số mũ nguyên
Cho \(n\) là một số nguyên dương.
– Với \(a\) là số thực tùy ý, lũy thừa bậc \(n\) của \(a\) là tích của \(n\) thừa số \(a\): \({a^n} = \underbrace {a.a……a}_n\)
– Với \(a\ne0\):
\(a^0=1\)
\(a^{-n}=\frac{1}{a^n}\)
Trong biểu thức \(a^m\), ta gọi \(a\) là cơ số, số nguyên \(m\) là số mũ.
Chú ý: \(0^0\) và \(0^n\) không có nghĩa. Lũy thừa với số mũ nguyên có các tính chất tương tự của lũy thừa với số mũ nguyên dương.
b) Lũy thừa với số mũ hữu tỉ
Cho \(a\) là số thực dương và số hữu tỉ \(r=\frac{m}{n}\) trong đó \(m\in\mathbb{Z},n\in\mathbb{N},n\geq 2.\) Lũy thừa với số mũ \(r\) là số \(a^r\) xác đinh bởi: \({a^r} = {a^{\frac{m}{n}}} = \sqrt[n]{{{a^m}}}\).
c) Lũy thừa với số mũ thực
Cho \(a\) là một số dương, \(\alpha\) là một số vô tỉ:
Ta gọi giới hạn của dãy số \(\left( {{a^{{r_n}}}} \right)\) là lũy thừa của \(a\) với số mũ \(\alpha\), kí hiệu là \(a^{\alpha}.\)
\({a^\alpha } = \mathop {\lim }\limits_{n \to + \infty } {a^{{r_n}}}\) với \(a = \mathop {\lim }\limits_{n \to + \infty } {r_n}\).
2. Các tính chất quan trọng của lũy thừa
Với số thực \(a>0\) ta có các tính chất sau:
\(a^x.a^y=a^{x+y} \ \ \ x, y\in \mathbb{R}\)
\(\frac{a^x}{a^y}=a^{x-y} \ \ \ x, y \in \mathbb{R}\)
\((a^x)^y=a^{xy} \ \ \ x,y\in R\)
\(\sqrt[x]{a^y}=a^{\frac{y}{x}} \ \ \ x\in N, x\geq 2, y\in R\)
\((a.b)^x=a^x.b^x\)
\(\left ( \frac{a}{b} \right )^y=\frac{a^y}{b^y}\)
3. So sánh hai lũy thừa
Cho số thực \(a\):
– Nếu \(a>1\) thì \(a^x > a^y\Leftrightarrow x>y\).
– Nếu \(0<a<1\) thì \(a^x > a^y\Leftrightarrow x<y\).
Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong phần hoạt động của học sinh sgk Giải tích 12.
Câu hỏi
1. Trả lời câu hỏi 1 trang 50 sgk Giải tích 12
Tính: \({(1,5)^4},{({{ – 2} \over 3})^3},{(\sqrt 3 )^5}\)
Trả lời:
Ta có:
\(\eqalign{
& {(1,5)^4} = 5.0625 \cr
& {({{ – 2} \over 3})^3} = {{ – 8} \over {27}} \cr
& {(\sqrt 3 )^5} = 9\sqrt 3 \cr} \)
2. Trả lời câu hỏi 2 trang 51 sgk Giải tích 12
Dựa vào đồ thị của các hàm số $y = x^3$ và $y = x^4$ (H.26, H.27), hãy biện luận theo $b$ số nghiệm của các phương trình $x^3 = b$ và $x^4 = b$.
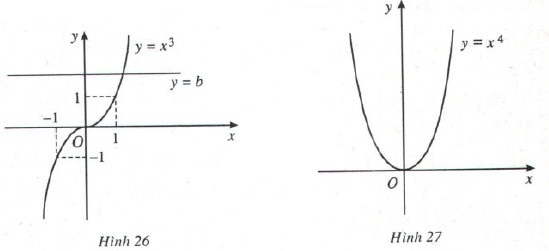
Trả lời:
– Số nghiệm của phương trình $x^3 = b$ là số giao điểm của hai đồ thị hàm số $y = b$ và $y = x^3.$
Dựa vào H.26 ta có đồ thị hàm số $y = x^3 $ luôn cắt đường thẳng $y = b$ tại một điểm duy nhất với mọi $b$ nên phương trình $x^3 = b $ luôn có nghiệm duy nhất với mọi $b$.
– Số nghiệm của phương trình $x^4 = b (1)$ là số giao điểm của hai đồ thị hàm số $y = b$ và $y = x^4.$
Dựa và hình 27 ta có:
+ Với $b < 0$ hai đồ thị hàm số trên không giao nhau, vậy phương trình (1) vô nghiệm.
+ Với $b = 0$, hai đồ thị hàm số tiếp xúc nhau tại $(0,0)$, vậy phương trình (1) có nghiệm duy nhất $x = 0$.
+ Với $b > 0$, hai đồ thị hàm số cắt nhau tại hai điểm phân biết, vậy phương trình (1) có hai nghiệm phân biệt.
3. Trả lời câu hỏi 3 trang 53 sgk Giải tích 12
Chứng minh tính chất: \(\root n \of a .\root n \of b = \root n \of {ab} \)
Trả lời:
Đặt \(\root n \of a = x;\,\root n \of b = y\).
Khi đó: \({x^n} = a;\,\,{y^n} = b\)
Ta có \({(xy)^n} = {x^n}.{y^n} = a.b\). Vậy $xy$ là căn bậc $n$ của $ab$.
Suy ra \(\root n \of {ab} = xy = \root n \of a .\root n \of b \)
4. Trả lời câu hỏi 4 trang 55 sgk Giải tích 12
Hãy nhắc lại các tính chất của lũy thừa với số mũ nguyên dương.
Trả lời:
Với \(m,n \in N^*\) ta có các tính chất sau đây:
– Các tính chất về đẳng thức:
\(\eqalign{
& 1.\,\,{a^m}.{a^n} = {a^{m + n}} \cr
& 2.\,\,{a^m}:{a^n} = {a^{m – n}}(m \ge n) \cr
& 3.\,\,{({a^m})^n} = {a^{m.n}} \cr
& 4.{({a \over b})^m} = {{{a^m}} \over {{b^m}}}\,\,\,(b \ne 0) \cr
& 5.\,{(ab)^m} = {a^m}.{b^n} \cr} \)
– Các tính chất về bất đẳng thức:
Với \(a > 1\) thì \(a^m> a^n⇔ m > n\).
Với \(0 < a < 1\) thì \(a^m> a^n⇔ m < n\).
Với \(0 < a < b\) thì \(a^m> b^m\)
5. Trả lời câu hỏi 5 trang 56 sgk Giải tích 12
Rút gọn biểu thức \({{(a^{\sqrt 3 – 1})^{\sqrt 3 – 1}} \over {a^{\sqrt 5 – 3}.a^{4 – \sqrt 5}}} (a > 0)\)
Trả lời:
Ta có:
\({{(a^{\sqrt 3 – 1})^{\sqrt 3 – 1}} \over {a^{\sqrt 5 – 3}.a^{4 – \sqrt 5}}}\) = \({a^{(\sqrt 3 – 1).(\sqrt 3 – 1)}} \over {a^{\sqrt 5 – 3 + 4 – \sqrt 5}}\) = \({a^{(3-1)} \over a^1}\) = \(a\)
6. Trả lời câu hỏi 6 trang 56 sgk Giải tích 12
So sánh các số: \({({3 \over 4})^{\sqrt 8 }}\,;\,\,{({3 \over 4})^3}\,\)
Trả lời:
Ta có:
\(\left\{ \matrix{
0 < {3 \over 4} < 1 \hfill \cr
\sqrt 8 < 3 \hfill \cr} \right. \Rightarrow {({3 \over 4})^{\sqrt 8 }} > {({3 \over 4})^3}\)
Dưới đây là Hướng dẫn giải bài 1 2 3 4 5 trang 56 57 sgk Giải tích 12. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!
Bài tập
Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập giải tích 12 kèm bài giải chi tiết bài 1 2 3 4 5 trang 56 57 sgk Giải tích 12 của Bài §1. Lũy thừa trong Chương 2. Hàm số lũy thừa. Hàm số mũ và Hàm số lôgarit cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

1. Giải bài 1 trang 56 sgk Giải tích 12
Tính:
a) $9^{\frac{2}{5}}.27^{\frac{2}{5}}$;
b) $144^{\frac{3}{4}}.9^{\frac{3}{4}}$;
c) $(\frac{1}{16})^{-0,75}+0,25^{\frac{-5}{2}}$;
d) $(0,04)^{-1,5}-(0,125)^{-\frac{2}{3}}$.
Bài giải:
Áp dụng các tính chất của hàm lũy thừa, ta có:
a) $9^{\frac{2}{5}}.27^{\frac{2}{5}}$ = $(9.27)^{\frac{2}{5}}$
= $(3^{2}.3^{3})^{\frac{2}{5}}$ = $(3^{2+3})^{\frac{2}{5}}$
= $(3^5)^{\frac{2}{5}}$ = $3^{2}=9$
Vậy $9^{\frac{2}{5}}.27^{\frac{2}{5}}=9$
b) $144^{\frac{3}{4}}.9^{\frac{3}{4}}$ = $(\frac{144}{9})^{\frac{3}{4}}$
= $16^{\frac{3}{4}}$ = $(2^{4})^{\frac{3}{4}}$ = $2^{3}=8$
Vậy $144^{\frac{3}{4}}.9^{\frac{3}{4}}=8$
c) $(\frac{1}{16})^{-0,75}+0,25^{\frac{-5}{2}}$ = $16^{0,75}+(\frac{1}{4})^{-\frac{5}{2}}$
= $16^{\frac{3}{4}}+4^{\frac{5}{2}}$ = $(2^{4})^{\frac{3}{4}}+(2^{2})^{\frac{5}{2}}$
= $2^{3}+2^{5}=8+32=40$
Vậy $(\frac{1}{16})^{-0,75}+0,25^{\frac{-5}{2}}=40$
d) $(0,04)^{-1,5}-(0,125)^{-\frac{2}{3}}$ = $(\frac{4}{100})^{-\frac{3}{2}}-(\frac{1}{8})^{-\frac{2}{3}}$
= $(\frac{100}{4})^{\frac{2}{3}}-8^{\frac{2}{3}}$ = $(5^{2})^{\frac{2}{3}}-(2^{3})^{\frac{2}{3}}$
= $5^{3}-2^{2}=125-4=121$
Vậy $(0,04)^{-1,5}-(0,125)^{-\frac{2}{3}}=121$
2. Giải bài 2 trang 56 sgk Giải tích 12
Viết các biểu thức sau dưới dạng lũy thừa với số mũ hữu tỉ:
a) $a^{\frac{1}{3}}.\sqrt{a}$;
b) $b^{\frac{1}{2}}.b^{\frac{1}{3}}.\sqrt[6]{b}$;
c) $a^{\frac{4}{3}}:\sqrt[3]{a}$;
d) $\sqrt[3]{b}:b^{\frac{1}{6}}$.
Bài giải:
Áp dụng công thức lũy thừa, ta có:
a) $a^{\frac{1}{3}}.\sqrt{a}$ = $a^{\frac{1}{3}}.a^{\frac{1}{2}}$
= $a^{\frac{1}{3}+\frac{1}{2}}=a^{\frac{5}{6}}$
Vậy $a^{\frac{1}{3}}.\sqrt{a}=a^{\frac{5}{6}}$
b) $b^{\frac{1}{2}}.b^{\frac{1}{3}}.\sqrt[6]{b}$ = $b^{\frac{1}{2}}.b^{\frac{1}{3}}.b^{\frac{1}{6}}$
= $b^{\frac{1}{2}+\frac{1}{3}+\frac{1}{6}}=b$
Vậy $b^{\frac{1}{2}}.b^{\frac{1}{3}}.\sqrt[6]{b}=b$
c) $a^{\frac{4}{3}}:\sqrt[3]{a}$ = $a^{\frac{4}{3}}:a^{\frac{1}{3}}$
= $a^{\frac{4}{3}-\frac{1}{3}}=a$
Vậy $a^{\frac{4}{3}}:\sqrt[3]{a}=a$
d) $\sqrt[3]{b}:b^{\frac{1}{6}}$ = $b^{\frac{1}{3}}:b^{\frac{1}{6}}$
= $b^{\frac{1}{3}-\frac{1}{6}}=b^{\frac{1}{6}}$
Vậy $\sqrt[3]{b}:b^{\frac{1}{6}}=b^{\frac{1}{6}}$
3. Giải bài 3 trang 57 sgk Giải tích 12
Viết các số sau theo thứ tự tăng dần:
a) $1^{3,75};2^{-1};(\frac{1}{2})^{-3}$
b) $98^{0};(\frac{3}{7})^{-1};32^{\frac{1}{5}}$
Bài giải:
Ta có:
a) $1^{3,75}=1$
$2^{-1}=\frac{1}{2}$
$(\frac{1}{2})^{-3}=2^{3}$
⇒ Thứ tự sắp xếp tăng dần:
$2^{-1}<1^{3,75}<(\frac{1}{2})^{-3}$
b) $98^{0}=1$
$(\frac{3}{7})^{-1}=\frac{7}{7}$
$32^{\frac{1}{5}}=2$
⇒ Thứ tự sắp xếp tăng dần:
$98^{0}<32^{\frac{1}{5}}<(\frac{3}{7})^{-1}$
4. Giải bài 4 trang 57 sgk Giải tích 12
Rút gọn các biểu thức sau:
a) $\frac{a^{\frac{4}{3}}(a^{-\frac{1}{3}}+a^{\frac{2}{3}})}{a^{\frac{1}{4}}(a^{\frac{3}{4}}+a^{-\frac{1}{4}})}$;
b) $\frac{b^{\frac{1}{5}}(\sqrt[5]{b^{4}}-\sqrt[5]{b^{-1}})}{b^{\frac{2}{3}}(\sqrt[3]{b}-\sqrt[3]{b^{-2}})}$;
c) $\frac{a^{\frac{1}{3}}b^{-\frac{1}{3}}-a^{-\frac{1}{3}}b^{\frac{1}{3}}}{\sqrt[3]{a^{2}}-\sqrt[3]{b^{2}}}$;
d) $\frac{a^{\frac{1}{3}}\sqrt{b}+b^{\frac{1}{3}}\sqrt{a}}{\sqrt[6]{a}+\sqrt[6]{b}}$.
Bài giải:
a) $\frac{a^{\frac{4}{3}}(a^{-\frac{1}{3}}+a^{\frac{2}{3}})}{a^{\frac{1}{4}}(a^{\frac{3}{4}}+a^{-\frac{1}{4}})}$
= $\frac{a^{\frac{4}{3}}.a^{-\frac{1}{3}}+a^{\frac{4}{3}}.a^{\frac{2}{3}}}{a^{\frac{1}{4}}.a^{\frac{3}{4}}+a^{\frac{1}{4}}.a^{-\frac{1}{4}}}$
= $\frac{a^{\frac{4}{3}-\frac{1}{3}}+a^{\frac{4}{3}+\frac{2}{3}}}{a^{\frac{1}{4}+\frac{3}{4}}+a^{\frac{1}{4}-\frac{1}{4}}}$
= $\frac{a+a^{2}}{a+1}=\frac{a(a+1)}{a+1}=a$
Vậy $\frac{a^{\frac{4}{3}}(a^{-\frac{1}{3}}+a^{\frac{2}{3}})}{a^{\frac{1}{4}}(a^{\frac{3}{4}}+a^{-\frac{1}{4}})}=a$
b) $\frac{b^{\frac{1}{5}}(\sqrt[5]{b^{4}}-\sqrt[5]{b^{-1}})}{b^{\frac{2}{3}}(\sqrt[3]{b}-\sqrt[3]{b^{-2}})}$
= $\frac{b^{\frac{1}{5}}.b^{\frac{1}{4}}-b^{\frac{1}{5}}.b^{-\frac{1}{5}}}{b^{\frac{2}{3}}.b^{\frac{1}{3}}-b^{\frac{2}{3}}.b^{-\frac{2}{3}}}$
= $\frac{b-1}{b-1}=1$
Vậy $\frac{b^{\frac{1}{5}}(\sqrt[5]{b^{4}}-\sqrt[5]{b^{-1}})}{b^{\frac{2}{3}}(\sqrt[3]{b}-\sqrt[3]{b^{-2}})}=1$
c) $\frac{a^{\frac{1}{3}}b^{-\frac{1}{3}}-a^{-\frac{1}{3}}b^{\frac{1}{3}}}{\sqrt[3]{a^{2}}-\sqrt[3]{b^{2}}}$
= $\frac{a^{\frac{2}{3}-\frac{1}{3}}b^{\frac{-1}{3}}-a^{\frac{-1}{2}}b^{\frac{2}{3}-\frac{1}{3}}}{a^{\frac{1}{6}}+a^{\frac{1}{6}}}$
= $(ab)^{\frac{-1}{3}}=\frac{1}{\sqrt[3]{ab}}$
Vậy $\frac{a^{\frac{1}{3}}b^{-\frac{1}{3}}-a^{-\frac{1}{3}}b^{\frac{1}{3}}}{\sqrt[3]{a^{2}}-\sqrt[3]{b^{2}}}=\frac{1}{\sqrt[3]{ab}}$
d) $\frac{a^{\frac{1}{3}}\sqrt{b}+b^{\frac{1}{3}}\sqrt{a}}{\sqrt[6]{a}+\sqrt[6]{b}}$
= $\frac{a^{\frac{1}{3}}.b^{\frac{1}{2}}+b^{\frac{1}{3}}.a^{\frac{1}{2}}}{a^{\frac{1}{6}}+b^{\frac{1}{6}}}$
= $\frac{(ab)^{\frac{1}{3}}\left [ b^{\frac{1}{6}}+a^{\frac{1}{6}} \right ]}{a^{\frac{1}{6}}+b^{\frac{1}{6}}}=\sqrt[3]{ab}$
Vậy $\frac{a^{\frac{1}{3}}\sqrt{b}+b^{\frac{1}{3}}\sqrt{a}}{\sqrt[6]{a}+\sqrt[6]{b}}=\sqrt[3]{ab}$
5. Giải bài 5 trang 57 sgk Giải tích 12
Chứng minh rằng:
a) $(\frac{1}{3})^{2\sqrt{5}}<(\frac{1}{3})^{3\sqrt{2}}$; b) $7^{6\sqrt{3}}>7^{3\sqrt{6}}$
Bài giải:
Ta có:
a) $2\sqrt{5}=\sqrt{2^{2}.5}=\sqrt{20}$
$3\sqrt{2}=\sqrt{3^{2}.2}=\sqrt{18}$
Mà $\sqrt{18}<\sqrt{20}$
⇒ $2\sqrt{5}>3\sqrt{2}$ và $0<\frac{1}{3}<1$
⇒ $(\frac{1}{3})^{2\sqrt{5}}<(\frac{1}{3})^{3\sqrt{2}}$. ( đpcm)
b) $6\sqrt{3}=\sqrt{6^{2}.3}=\sqrt{108}$
$3\sqrt{6}=\sqrt{3^{2}.6}=\sqrt{54}$
Mà $\sqrt{54}<\sqrt{108}$
⇒ $3\sqrt{6}<6\sqrt{3}$
⇒ $7^{6\sqrt{3}}>7^{3\sqrt{6}}$. (đpcm)
Bài trước:
- Ôn tập chương 1: Giải bài 1 2 3 4 5 6 7 8 9 10 11 12 trang 45 46 47 sgk Giải tích 12
- Ôn tập chương 1: Giải bài tập trắc nghiệm 1 2 3 4 5 trang 47 48 sgk Giải tích 12
Bài tiếp theo:
Xem thêm:
- Các bài toán 12 khác
- Để học tốt môn Vật lí lớp 12
- Để học tốt môn Sinh học lớp 12
- Để học tốt môn Ngữ văn lớp 12
- Để học tốt môn Lịch sử lớp 12
- Để học tốt môn Địa lí lớp 12
- Để học tốt môn Tiếng Anh lớp 12
- Để học tốt môn Tiếng Anh lớp 12 thí điểm
- Để học tốt môn Tin học lớp 12
- Để học tốt môn GDCD lớp 12
Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 12 với giải bài 1 2 3 4 5 trang 56 57 sgk Giải tích 12!
“Bài tập nào khó đã có giaibaisgk.com“
