Hướng dẫn Giải bài 1 2 3 4 5 trang 9 10 sgk Giải tích 12

Nội Dung

Hướng dẫn giải Bài §1. Sự đồng biến, nghịch biến của hàm số, Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số, sách giáo khoa Giải tích 12. Nội dung bài giải bài 1 2 3 4 5 trang 9 10 sgk Giải tích 12 bao gồm tổng hợp công thức, lý thuyết, phương pháp giải bài tập giải tích có trong SGK để giúp các em học sinh học tốt môn toán lớp 12.

Lý thuyết

1. Định nghĩa

Kí hiệu: K là một khoảng, một đoạn hoặc một nửa khoảng.

Cho hàm số $y=f(x)$ xác định trên $K$.

– Hàm số $y=f(x)$ đồng biến (tăng) trên K nếu

$\left\{ {\begin{array}{*{20}{c}} {{x_1},{x_2} \in K}\\ {{x_1} < {x_2}} \end{array}} \right. \Rightarrow f({x_1}) < f({x_2})$.

– Hàm số $y=f(x)$ nghịch biến (giảm) trên $K$ nếu

$\left\{ {\begin{array}{*{20}{c}} {{x_1},{x_2} \in K}\\ {{x_1} < {x_2}} \end{array}} \right. \Rightarrow f({x_1}) > f({x_2})$.

2. Điều kiện cần để hàm số đơn điệu

Cho hàm số $y=f(x)$ có đạo hàm trên $K$:

– Nếu $f(x)$ đồng biến trên $K$ thì $f'(x)\geq 0$ với mọi $x\in K$.

– Nếu $f(x)$ nghịch biến trên $K$ thì $f'(x)\leq 0$ với mọi $x\in K$.

3. Điều kiện đủ để hàm số đơn điệu

Cho hàm số $y=f(x)$ có đạo hàm trên K:

– Nếu $f'(x)\geq 0$ với mọi $x\in K$ và $f'(x)=0$ chỉ tại một số hữu hạn điểm thuộc K thì $f(x)$ đồng biến trên K.

– Nếu $f'(x)\leq 0$ với mọi $x\in K$ và $f'(x)=0$ chỉ tại một số hữu hạn điểm thuộc K thì $f(x)$ nghịch biến trên K.

– Nếu $f'(x)=0$ với mọi $x\in K$ thì $f(x)$ là hàm hằng trên K.

4. Các bước xét tính đơn điệu của hàm số

– Bước 1: Tìm tập xác định.

– Bước 2: Tính đạo hàm $f'(x)=0$. Tìm các điểm $x_i$ (i= 1 , 2 ,…, n) mà tại đó đạo hàm bằng 0 hoặc không xác định.

– Bước 3: Sắp xếp các điểm x_i theo thứ tự tăng dần và lập bảng biến thiên.

– Bước 4: Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.

Dưới đây là phần Hướng dẫn trả lời các câu hỏi và bài tập trong phần hoạt động của học sinh sgk Giải tích 12.

Câu hỏi

1. Trả lời câu hỏi 1 trang 4 sgk Giải tích 12

Từ đồ thị (H.1, H.2) hãy chỉ ra các khoảng tăng, giảm của hàm số $y = \cos x$ trên đoạn $\displaystyle \left[ {{{ – \pi } \over 2};\,{{3\pi } \over 2}} \right]$ và các hàm số $\displaystyle y = \left| x \right|$ trên khoảng $\displaystyle \left( { – \infty ; + \infty } \right)$.

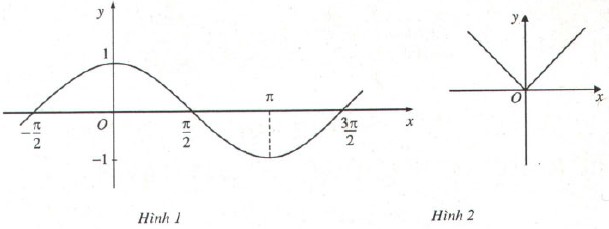
Trả lời:

♦ Hàm số $y = \cos x$ trên đoạn $\displaystyle \left[ {{{ – \pi } \over 2};\,{{3\pi } \over 2}} \right]$

Các khoảng tăng: $\displaystyle \left( {{{ – \pi } \over 2};\,0} \right);\,\left( {\pi ;\,{{3\pi } \over 2}} \right)$

Các khoảng giảm: $\displaystyle \left( {0;\pi } \right)$.

♦ Hàm số $\displaystyle y = \left| x \right|$ trên khoảng $\displaystyle \left( { – \infty ; + \infty } \right)$

Khoảng tăng: $\displaystyle \left[ {0, + \infty } \right)$

Khoảng giảm $\displaystyle \left( { – \infty ,0} \right]$

2. Trả lời câu hỏi 2 trang 5 sgk Giải tích 12

Xét các hàm số sau và đồ thị của chúng:

Trả lời:

a) Hàm số: $y = \,{{ – {x^2}} \over 2}$ (H.4a)

b) Hàm số: $y = \,{1 \over x}$ (H.4b) (H.4b)

Hàm số đồng biến khi dấu của đạo hàm là “+” và nghịch biến khi dấu của đạo hàm là “-“.

3. Trả lời câu hỏi 3 trang 7 sgk Giải tích 12

Khẳng định ngược lại với định lí trên có đúng không ? Nói cách khác, nếu hàm số đồng biến (nghịch biến) trên $K$ thì đạo hàm của nó có nhất thiết phải dương (âm) trên đó hay không ?

Trả lời:

Xét hàm số $y = x^3$ có đạo hàm $y’ = 3x^2 ≥ 0$ với mọi số thực $x$ và hàm số đồng biến trên toàn bộ $R$. Vậy khẳng định ngược lại với định lý trên chưa chắc đúng hay nếu hàm số đồng biến (nghịch biến) trên $K$ thì đạo hàm của nó không nhất thiết phải dương (âm) trên đó.

Dưới đây là Hướng dẫn giải bài 1 2 3 4 5 trang 9 10 sgk Giải tích 12. Các bạn hãy đọc kỹ đầu bài trước khi giải nhé!

Bài tập

Giaibaisgk.com giới thiệu với các bạn đầy đủ phương pháp giải bài tập giải tích 12 kèm bài giải chi tiết bài 1 2 3 4 5 trang 9 10 sgk Giải tích 12 của Bài §1. Sự đồng biến, nghịch biến của hàm số trong Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số cho các bạn tham khảo. Nội dung chi tiết bài giải từng bài tập các bạn xem dưới đây:

Giải bài 1 2 3 4 5 trang 9 10 sgk Giải tích 12

1. Giải bài 1 trang 9 sgk Giải tích 12

Xét sự đồng biến, nghịch biến của các hàm số:

a) $y = 4 + 3x – x^2$.

b) $y =\frac{1}{3} x^3 + 3x^2 – 7x – 2$.

c) $y = x^4 – 2x^2 + 3$.

d) $y = -x^3 + x^2 – 5$.

Bài giải:

a) Xét hàm số $y = 4 + 3x – x^2$

– Tập xác định: $D=\mathbb{R};$

$y’ = 3 – 2x \Rightarrow y’ = 0 \Leftrightarrow 3-2x=0\Leftrightarrow x = \frac{3}{2}$.

Với $x=\frac{3}{2}\Rightarrow y=\frac{25}{4}$

– Bảng biến thiên:

Từ bảng biến thiên ta thấy: Hàm số đồng biến trên khoảng ($-\infty$; $\frac{3}{2}$) và nghịch biến trên khoảng ($\frac{3}{2}$; $+\infty$).

b) Xét hàm số $y =\frac{1}{3} x^3 + 3x^2 – 7x – 2$

– Tập xác định: $D=\mathbb{R};$

$y’ = {x^2} + 6x – 7 \Rightarrow y’ = 0 \Leftrightarrow \left[ \begin{array}{l} x = 1\\ x = – 7 \end{array} \right..$

Với $x=-7 \Rightarrow y=\frac{239}{3}$

Với $x=1 \Rightarrow y=-\frac{17}{3}$

– Bảng biến thiên:

Từ bảng biến thiên ta thấy: Hàm số đồng biến trên các khoảng ($-\infty$ ; -7), (1 ; $+\infty$) và nghịch biến trên khoảng (-7;1).

c) Xét hàm số $y = x^4 – 2x^2 + 3$

– Tập xác định: $D=\mathbb{R};$

$\begin{array}{l} y’ = 4{x^3} – 4x = 4x({x^2} – 1)\\ y’ = 0 \Leftrightarrow 4x({x^2} – 1) \Leftrightarrow \left[ \begin{array}{l} x = – 1\\ x = 0\\ x = 1 \end{array} \right. \end{array}$

Với $x=-1$ ta có $y=2$.

Với $x=0$ ta có $y=3$.

Với $x=1$ ta có $y=2$.

– Bảng biến thiên:

Từ bảng biến thiên ta thấy: Hàm số đồng biến trên các khoảng $(-1 ; 0), (1 ; +\infty)$; nghịch biến trên các khoảng $(-\infty; -1), (0 ; 1)$.

d) Xét hàm số $y = -x^3 + x^2 – 5$

– Tập xác định: $D=\mathbb{R};$

$\begin{array}{l} y’ = – 3{x^2} + 2x\\ y’ = 0 \Leftrightarrow – 3{x^2} + 2x \Leftrightarrow \left[ \begin{array}{l} x = 0\\ x = \frac{2}{3} \end{array} \right. \end{array}$

Với $x=0\Rightarrow y=-5.$

Với $x=\frac{2}{3}\Rightarrow -\frac{131}{27}.$

– Bảng biến thiên:

Từ bảng biến thiên ta thấy: Hàm số đồng biến trên khoảng $( 0 ; \frac{2}{3} )$ và nghịch biến trên các khoảng $(-\infty; 0), ( \frac{2}{3}; +\infty).$

2. Giải bài 2 trang 10 sgk Giải tích 12

Tìm các khoảng đơn điệu của các hàm số:

a) $y=\frac{3x+1}{1-x}$ ;

b) $y=\frac{x^{2}-2x}{1-x}$ ;

c) $y=\sqrt{x^{2}-x-20}$ ;

d) $y=\frac{2x}{x^{2}-9}$.

Bài giải:

a) Xét hàm số $y=\frac{3x+1}{1-x}$

Tập xác định:$D = \mathbb{R} \setminus \left \{ 1 \right \}$ .

$y’=\frac{4}{(1-x)^{2}}> 0, \forall x \neq 1$.

Bảng biến thiên:

Vậy hàm số đồng biến trên các khoảng: $( -\infty; 1), (1 ; +\infty)$.

b) Xét hàm số $y=\frac{x^{2}-2x}{1-x}$

Tập xác định: $D = \mathbb{R} \setminus \left \{ 1 \right \}$.

$y’=\frac{-x^{2}+2x-2}{(1-x)^{2}}< 0, \forall x \neq 1$ .

Bảng biến thiên:

Vậy hàm số nghịch biến trên các khoảng: $(-\infty ; 1), (1 ; +\infty)$.

c) Xét hàm số $y=\sqrt{x^{2}-x-20}$

– Tập xác định: $D = (-\infty$;-4] ∪ [5 ;$+\infty)$.

$y’=\frac{2x-1}{2\sqrt{x^{2}-x-20}}, \forall x \in (-\infty ; -4) \cup (5 ; +\infty)$.

– Bảng biến thiên:

Vậy hàm số nghịch biến trên khoảng $(-\infty ; -4)$ và đồng biến trên khoảng $(5 ; +\infty)$.

d) Xét hàm số $y=\frac{2x}{x^{2}-9}$

– Tập xác định: $D = \mathbb{R} \setminus \left \{ -3 ; 3 \right \}$.

$y’=\frac{-2(x^{2}+9)}{\left (x^{2}-9 \right )^{2}} < 0, \forall x \in D.$

– Bảng biến thiên:

Vậy hàm số nghịch biến trên các khoảng : $(-\infty ; -3), (-3 ; 3), (3 ; +\infty)$.

3. Giải bài 3 trang 10 sgk Giải tích 12

Chứng minh rằng hàm số $y=\frac{x}{x^{2}+1}$ đồng biến trên khoảng (-1;1) và nghịch biến trên các khoảng $(-\infty; -1)$ và $(1 ; +\infty)$.

Bài giải:

Xét hàm số $y=\frac{x}{x^{2}+1}$

– Tập xác định: $D=\mathbb{R}.$

$y’ = \left( {\frac{x}{{{x^2} + 1}}} \right)’ = \frac{{x'({x^2} + 1) – ({x^2} + 1)’x}}{{{{({x^2} + 1)}^2}}}$

$= \frac{{{x^2} + 1 – 2{x^2}}}{{{{({x^2} + 1)}^2}}} = \frac{{1 – {x^2}}}{{{{({x^2} + 1)}^2}}}.$

$y’ = 0 \Leftrightarrow \frac{{1 – {x^2}}}{{{{({x^2} + 1)}^2}}} \Leftrightarrow 1 – {x^2} \Leftrightarrow \left[ \begin{array}{l} x = – 1\\ x = 1 \end{array} \right.$

Với $x=-1\Rightarrow y=-\frac{1}{2}$.

Với $x=1\Rightarrow y=\frac{1}{2}$

– Bảng biến thiên:

Từ bảng biến thiên ta thấy: Hàm số đồng biến trên khoảng $(-1; 1)$; nghịch biến trên các khoảng $(-\infty; -1), (1; +\infty).$

4. Giải bài 4 trang 10 sgk Giải tích 12

Chứng minh rằng hàm số $y=\sqrt{2x-x^{2}}$ đồng biến trên khoảng $(0 ; 1)$ và nghịch biến trên các khoảng $(1 ; 2)$.

Bài giải:

Xét hàm số $y=\sqrt{2x-x^{2}}$

– Tập xác định: $D = \left [ 0 ; 2 \right ];$

$y’ = \frac{{2 – 2x}}{{2\sqrt {2x – {x^2}} }} = \frac{{1 – x}}{{\sqrt {2x – {x^2}} }}$

$y’ = 0 \Leftrightarrow x = 1.$

– Bảng biến thiên:

Từ bảng biến thiên ta thấy: Hàm số đồng biến trên khoảng (0;1) và nghịch biến trên khoảng (1;2).

Vậy ta có điều phải chứng minh.

5. Giải bài 5 trang 10 sgk Giải tích 12

Chứng minh các bất đẳng thức sau:

a) $\tan x > x (0 < x <\frac{\pi }{2} )$

b) $\tan x > x +\frac{x^3}{3} (0 < x < \frac{\pi }{2})$

Bài giải:

a) $\tan x>x\ \ \left( 0<x<\frac{\pi }{2} \right).$

Xét hàm số: $y=f\left( x \right)=\tan x-x$ với $x\in \left( 0;\ \frac{\pi }{2} \right).$

Ta có: $y’=\frac{1}{{{\cos }^{2}}x}-1=\frac{1-{{\cos }^{2}}x}{{{\cos }^{2}}x}=\frac{{{\sin }^{2}}x}{{{\cos }^{2}}x}={{\tan }^{2}}x>0\forall x\in \left( 0;\frac{\pi }{2} \right)$

Vậy hàm số luôn đồng biến trên $\left( 0;\frac{\pi }{2} \right).$

$\Rightarrow \forall \ x\in \left( 0;\frac{\pi }{2} \right) \text{ta có} \, f\left( x \right)>f\left( 0 \right) \\ \Leftrightarrow \tan x-x>\tan 0-0 \\ \Leftrightarrow \tan x-x>0 \\ \Leftrightarrow \tan x>x\ \ \left(đpcm \right).$

b) $\tan x>x+\frac{{{x}^{3}}}{3}\ \ \left( 0<x<\frac{\pi }{2} \right).$

Xét hàm số: $y=g\left( x \right)=\tan x-x-\frac{{{x}^{3}}}{3}$ với $x\in \left( 0;\ \frac{\pi }{2} \right).$

Ta có: $y’=\frac{1}{{{\cos }^{2}}x}-1-{{x}^{2}}=1+{{\tan }^{2}}x-1-{{x}^{2}}\\ ={{\tan }^{2}}x-{{x}^{2}}=\left( \tan x-x \right)\left( \tan x+x \right).$

Với $\forall \ x\in \left( 0;\frac{\pi }{2} \right)\Rightarrow \tan x>0$ nên ta có: $\tan x+x>0$ và $\tan x-x>0$ (theo câu a) $\Rightarrow y’>0\,\,\forall x\in \left( 0;\frac{\pi }{2} \right)$

Vậy hàm số $y=g\left( x \right)$ đồng biến trên $\left( 0;\frac{\pi }{2} \right)\Rightarrow g\left( x \right)>g\left( 0 \right).$

$\Leftrightarrow \tan x-x-\frac{{{x}^{3}}}{3}>\tan 0-0-0 \\ \Leftrightarrow \tan x-x-\frac{{{x}^{3}}}{3}>0 \\ \Leftrightarrow \tan x>x+\frac{{{x}^{3}}}{3}\ \ \ \left(đpcm \right).$

Bài tiếp theo:

Giải bài 1 2 3 4 5 6 trang 18 sgk Giải tích 12

Xem thêm:

Chúc các bạn làm bài tốt cùng giải bài tập sgk toán lớp 12 với giải bài 1 2 3 4 5 trang 9 10 sgk Giải tích 12!

“Bài tập nào khó đã có giaibaisgk.com“